RECURSO PCDF (Escrivão): Matemática e Raciocínio Lógico
Fala, pessoal!
Sou o Eduardo Mocellin, professor de Matemática e de Raciocínio Lógico do Estratégia Concursos.
Neste artigo, disponibilizo um embasamento para que o candidato elabore um recurso para uma questão da prova da PCDF de 2021 para o cargo de Escrivão.
Antes de analisarmos a questão, convido você a me seguir no Instagram: @edu.mocellin
Vamos ao problema:
Seis pessoas devem se reunir em uma mesa redonda, mas duas delas não podem se sentar uma ao lado da outra. Nessa situação, a quantidade de maneiras distintas de essas seis pessoas sentarem em torno dessa mesa é superior a 400.
Gabarito do professor: ERRADO.
Gabarito preliminar da banca: CERTO.
Análise da justificativa da banca
Vejamos a justificativa apontada pela banca:

Observe que a banca se equivocou ao dizer que “uma das pessoas que tem restrição de posicionamento na mesa tem seis possibilidades de tomar assento nessa mesa“.
Isso porque, em uma disposição circular, a primeira pessoa inserida na mesa apenas cria um referencial.
Suponha que uma das pessoas que tem restrição de posicionamento é a pessoa A. Vamos inseri-la na mesa:
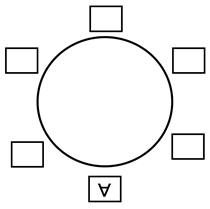
Note que, observando essa mesa de um outro ângulo (girando ela em 180 graus), temos a seguinte disposição:
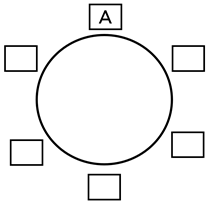
Em outras palavras, não existem seis possibilidades para se inserir a primeira pessoa pois, na verdade, essa pessoa criou apenas um referencial.
Considerando que há apenas uma forma de inserir a primeira pessoa, o restante do raciocínio da banca está correto. Portanto, o raciocínio correto seria o seguinte:
“Ao selecionar uma das pessoas que tem restrição de posicionamento na mesa, ela cria um referencial, havendo uma única possibilidade de ela tomar assento na mesa. A segunda pessoa com restrição, uma vez já fixado esse referencial, teria então três possibilidades de tomar assento à mesa. Portanto, as duas pessoas com restrição de posicionamento teriam 1 × 3 = 3 possibilidades de posicionamento. Como as outras quatro pessoas podem se sentar em qualquer local, então tem-se 3×4! = 3 × 24 = 72 possibilidades de essas pessoas tomarem assento à mesa.”
Outra forma de resolver o problema
Primeiramente, vamos desconsiderar a restrição de que duas pessoas não podem sentar lado a lado. Nesse caso, o número de possibilidades em que 6 pessoas podem se reunir em uma mesa redonda é a Permutação Circular de 6:
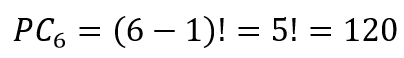
Desses 120 casos, devemos subtrair os casos em que as duas pessoas sentam juntas. Considere a seguinte disposição em que fixamos as pessoas A e B que não poderiam sentar juntas:
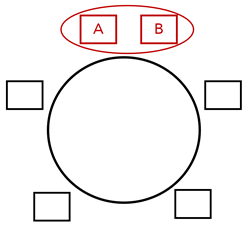
O número de possibilidades de as 6 pessoas sentarem com a disposição “A-B” é a permutação circular de 5 elementos:
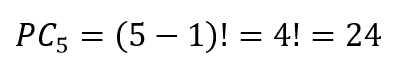
Veja essa nova disposição em que A e B sentam juntas: “B-A”.
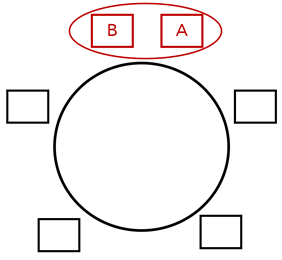
O número de possibilidades de as 6 pessoas sentarem com a disposição “B-A” também é a permutação circular de 5 elementos:
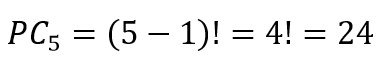
Logo, descontando todos os casos em que as duas pessoas não podem sentar juntas, ficamos com as 72 possibilidades já obtidas:
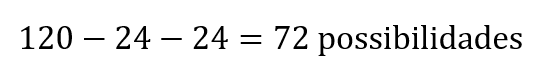
Em resumo, a resposta correta é:
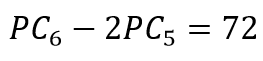
Logo, a quantidade de maneiras distintas de essas seis pessoas sentarem em torno dessa mesa é inferior a 400.
Considerações Finais
Espero que a explanação acima sirva como um bom embasamento para aqueles que desejam pleitear a mudança do gabarito. Até a próxima!
Instagram: @edu.mocellin