Oi pessoal! Tudo bem? O gabarito preliminar da PF saiu há pouco e acreditamos que existe possibilidade de recurso para uma questão. É a questão do bloco 40 – 42 que trata da esperança condicionada.
Aqui, vou resolver a questão de forma mais técnica e direta, utilizando 2 formas de resolução diferentes, no intuito de facilitar o trabalho daqueles que pretendem interpor recurso. Se preferir um passo a passo mais detalhado, dá uma olhadinha neste artigo que publicamos no dia da prova da PF com a resolução detalhada de todas as questões de Estatística.
Considere que X e Y sejam variáveis aleatórias contínuas que se distribuem conjuntamente conforme a função de densidade f(x,y) = x+y, na qual 0 < x < 1 e 0 < y < 1.
Com base nessas informações, julgue os itens seguintes.
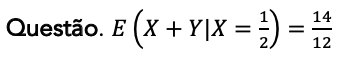
Comentários:
A esperança condicionada apresenta a propriedade aditiva:
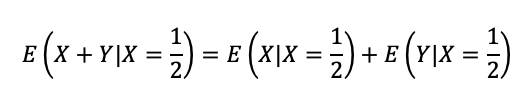
Sabendo que X=1/2, a esperança E(X|X=1/2) corresponde à esperança da constante X=1/2:
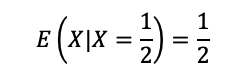
Logo, a esperança desejada é:
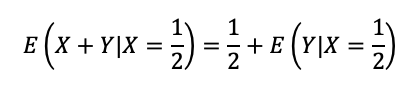
A esperança de Y condicionada a X = 1/2 é definida como:
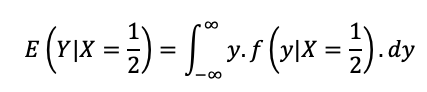
Em que f(y|X=1/2) é a razão entre a função densidade de probabilidade conjunta e a função densidade de probabilidade marginal de X=1/2:
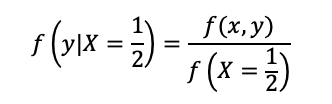
A função marginal de x é calculada por:
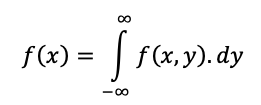
Sabendo que 0<y<1, temos:
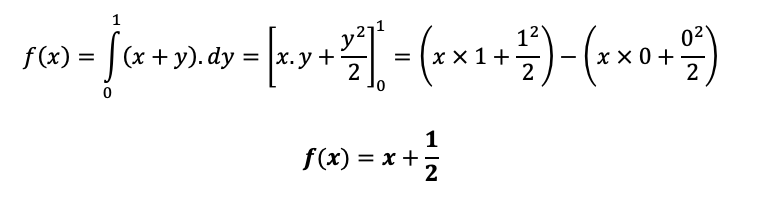
Então, o valor de f(X=1/2) é:
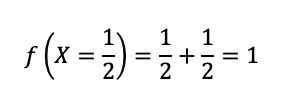
Portanto, a função de Y condicionada a X=1/2 é:
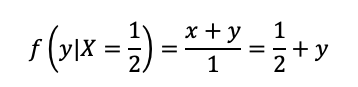
Agora, podemos calcular a esperança de Y condicionada a X=1/2:
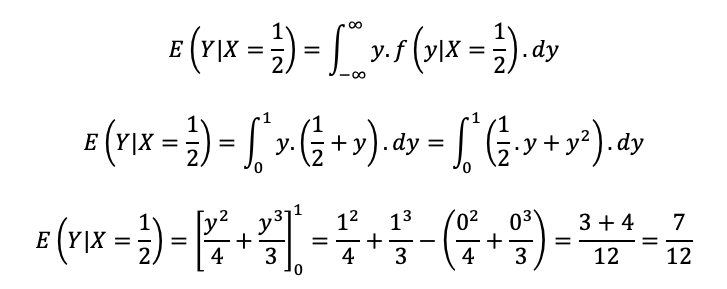
Por fim, somamos a esperança de X condicionada a X = 1/2:
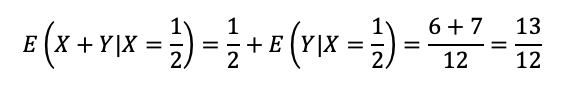
O resultado é diferente de 14/12.
Observação: em vez de utilizar a propriedade da esperança para separar a soma da esperança condicionada solicitada na questão, é possível calculá-la utilizando a própria integral da esperança condicionada:
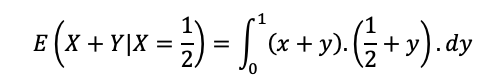
Sabendo que X=1/2, temos:
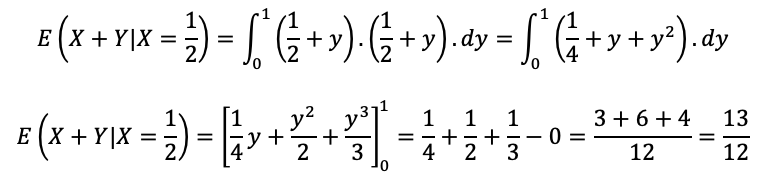
Com isso, obtemos o mesmo resultado encontrado anteriormente.
Assim, entendemos ser cabível recurso pleiteando a alteração de gabarito de “certo” para “ERRADO“.