Raciocínio Lógico TST e CLDF – editais idênticos!

Olá pessoal, tudo bem? Recentemente foram publicados os editais dos concursos do TST e da CLDF, ambos cobrando a disciplina de Raciocínio Lógico para o cargo de Técnico. Assim, resolvi escrever este artigo para passar algumas dicas que considero bem relevantes para a sua preparação. 

Para começar, vamos dar uma olhada no conteúdo cobrado pela banca FCC, organizadora de ambos os certames, para os cargos de Técnico Judiciário e de Técnico Legislativo. Trata-se exatamente dos mesmos assuntos:

Raciocínio Lógico-Matemático: Números inteiros e racionais: operações (adição, subtração, multiplicação, divisão, potenciação); expressões numéricas; múltiplos e divisores de números naturais; problemas. Frações e operações com frações. Números e grandezas proporcionais: razões e proporções; divisão em partes proporcionais; regra de três; porcentagem e problemas. Estrutura lógica de relações arbitrárias entre pessoas, lugares, objetos ou eventos fictícios; deduzir novas informações das relações fornecidas e avaliar as condições usadas para estabelecer a estrutura daquelas relações. Compreensão e elaboração da lógica das situações por meio de: raciocínio verbal, raciocínio matemático, raciocínio sequencial, orientação espacial e temporal, formação de conceitos, discriminação de elementos. Compreensão do processo lógico que, a partir de um conjunto de hipóteses, conduz, de forma válida, a conclusões determinadas.

Se você ficou com preguiça de ler este conteúdo inteiro, ou leu e não entendeu muita coisa, fique tranquilo rs… este é um conteúdo cobrado repetidamente pela banca FCC em diversos de seus concursos recentes, às vezes com pequenas variações. Como venho preparando materiais para praticamente todos esses concursos, acabei compreendendo bem o que a FCC quer dizer com cada frase deste edital, isto é, que tipo de questão de prova ela pretende cobrar. Podemos resumir este edital a apenas isto:

1. Conjuntos numéricos
2. Proporções e porcentagens
3. Estruturas lógicas
4. Lógica de proposições

Sim, esses são os QUATRO únicos assuntos que você precisa estudar para enfrentar a prova de Raciocínio Lógico do TST ou da CLDF. Um pequeno esclarecimento: talvez você não tenha entendido de onde eu tirei o tópico “Lógica de proposições” deste edital. Ele está contido nesta frase, que a FCC adora utilizar quando pretende cobrar as proposições lógicas:

 Compreensão do processo lógico que, a partir de um conjunto de hipóteses, conduz, de forma válida, a conclusões determinadas.

Como estudar Raciocínio Lógico para o TST e a CLDF

Eu tenho um artigo bastante completo aqui no Estratégia sobre COMO ESTUDAR RACIOCÍNIO LÓGICO PARA CONCURSOS. Recomendo que você o visite, lá tem várias informações úteis e aulas gratuitas. De qualquer forma, vou adiantar o que considero mais relevante para você aqui mesmo.

Quando falamos de Raciocínio Lógico, o que importa mesmo é que você seja capaz de acertar os exercícios de prova. E como você deve fazer para atingir este objetivo? Certamente você sabe que é preciso praticar bastante. Mas esta prática deve ser feita com MÉTODO. Isto é, você precisa:

1. ser apresentado aos conceitos teóricos que vão embasar a resolução de exercícios;
2. conhecer os principais modelos de exercícios cobrados pela FCC. Para isto, é preciso ser capaz de:

• IDENTIFICAR características de cada modelo de questão (afinal elas estarão “embaralhadas” em sua prova);
• dominar a RECEITA DE BOLO, isto é, o “procedimento padrão” para resolução de cada tipo de questão;

 

Cumpridos os passos acima, aí realmente só resta PRATICAR bastante. E, claro, é essencial que desde o momento inicial dos estudos você já comece a PREPARAR O MATERIAL DE REVISÃO. Vamos falar sobre isto?

 

Como revisar Raciocínio Lógico para o TST e a CLDF

Como você vai estudar ao longo de alguns meses para o seu concurso, é natural que você vá esquecendo parte do que você estudou. Para lembrar tudo no dia da prova (ou quase tudo), é essencial revisar diversas vezes o conteúdo estudado. No caso do Raciocínio Lógico,  acredito que a revisão fica muito fácil e eficiente se, durante o procedimento normal de estudo, você se preocupar em fazer 3 coisas: 

1. sublinhar os conceitos mais importantes do conteúdo teórico (e fazer marcações/anotações que julgar pertinentes);
2. marcar os exercícios mais difíceis do seu material, ou seja, aqueles que você não conseguiu fazer sozinho (ou fez com muita dificuldade) e aqueles que, mesmo tendo feito sozinho, você julgar que vale a pena marcar por se tratar de questões muito completas, que abordam mais de um ponto do edital. 
3. preparar um resumo de fórmulas, isto é, pegar uma ÚNICA folha de papel e anotar nela as principais fórmulas que você precisa decorar (no caso do TST/CLDF, recomendo anotar as principais negações e equivalências das proposições compostas, por exemplo).

Desta forma, fica muito fácil e produtivo fazer as suas revisões. Basta reler os conceitos sublinhados,  refazer os exercícios mais difíceis e relembrar as principais fórmulas anotadas. Você pode fazer isso várias vezes ao longo da sua preparação e, naturalmente, cada vez mais esses elementos vão ficando sedimentados na sua memória. 

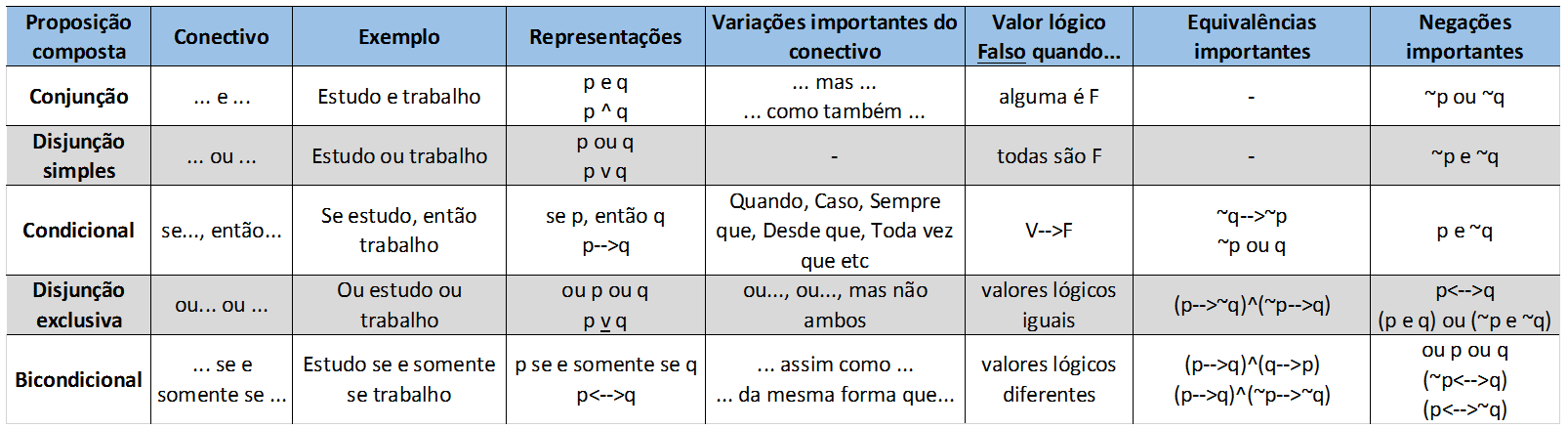
Para te dar uma ajuda, veja abaixo uma tabela contendo as principais informações sobre as Proposições Lógicas que você precisa guardar:

Durante as suas revisões, você também pode aproveitar para resolver AINDA MAIS questões. É por isso que eu incluo cerca de 500 questões resolvidas em nossos cursos completos de Raciocínio Lógico para o TST e para a CLDF. Você não precisa resolver todas logo na primeira passagem pelo conteúdo, mas pode deixar parte das questões de cada aula para resolver em momentos futuros, durante as suas revisões.

 

Praticando Raciocínio Lógico para o Concurso TST e Concurso CLDF

E, por falar em exercícios, que tal praticarmos um pouco?  Deixo abaixo a prova resolvida do TRT da 11ª Região, concurso recentíssimo da banca FCC e que teve edital IDÊNTICO ao conteúdo cobrado pelo TST e pela CLDF para os cargos de Técnico. Espero que você aproveite estas questões para compreender melhor o nível de exigência da banca FCC e fazer uma auto avaliação. Desta forma você saberá identificar melhor o quanto precisa (ou não) se dedicar à minha disciplina.

 

FCC – TRT/11 – 2017) Na festa de fim de ano de uma empresa estavam presentes X pessoas. Para agradar os participantes foram encomendados docinhos especiais. A ideia era dar 7 docinhos para cada pessoa presente, mas verificou-se que faltariam 19 docinhos. Se fossem dados 6 docinhos para cada pessoa, sobrariam 98 docinhos. O número de docinhos que haviam sido encomendados para essa festa era igual a

(A) 950.

(B) 100.

(C) 800.

(D) 750.

(E) 600.

RESOLUÇÃO: 

Com 7 docinhos por pessoa, faltariam 19 docinhos. Ou seja,

Docinhos = 7X – 19

Com 6 docinhos por pessoa, sobrariam 98. Ou seja:

Docinhos = 6X + 98

Igualando as quantidades de docinhos:

7X – 19 = 6X + 98

7X – 6X = 98 + 19

X = 117

Logo,

Docinhos = 7X – 19

Docinhos = 7×117 – 19

Docinhos = 819 – 19

Docinhos = 800

Resposta: C

FCC – TRT/11 – 2017) O valor que corresponde ao resultado correto da expressão numérica (13² – 11²) / (12² / 3) / (10² – 9² – 4²) é

a) 2/5

b) 1/4

c) 3/4

d) 1/5

e) 1/3

​RESOLUÇÃO: 

Devemos começar resolvendo as potências dentro de cada parênteses:

(13² – 11²) / (12² / 3) / (10² – 9² – 4²)  =

(169 – 121) / (144 / 3) / (100 – 81 – 16)

Agora resolvemos as demais operações dentro dos parênteses:

48 / 48 / 3 =

1 / 3

Resposta: E

FCC – TRT/11 – 2017) Um ciclista cumpriu seu trajeto de treinamento com uma velocidade média de 20 km/h e um tempo de 6 horas e 24 minutos. No dia seguinte, ao voltar, o ciclista cumpriu o mesmo trajeto em exatamente 8 horas. Nesse dia sua velocidade média caiu, em relação ao treinamento do dia anterior, um valor igual a

(A) 1,5 km/h.

(B) 3 km/h.

(C) 7 km/h.

(D) 4 km/h.

(E) 6 km/h.

​RESOLUÇÃO: 

Podemos escrever:

20km/h —————— 6h 24min

V km/h ——————– 8h

Transformando as horas para minutos, temos:

20km/h —————— 384 min

V km/h —————— 480 min

Quanto MAIOR a velocidade, MENOR o tempo. As grandezas são inversamente proporcionais. Invertendo uma coluna:

V km/h —————— 384 min

20 km/h ——————– 480 min

Montando a proporção:

V x 480 = 20 x 384

V x 24 = 384

V = 384 / 24

V = 16 km/h

A queda na velocidade foi de 20 – 16 = 4km/h

Resposta: D

FCC – TRT/11 – 2017) O preço de um sapato, após um aumento de 15%, é R$ 109,25. Se o preço do sapato não tivesse sofrido esse aumento de 15%, mas um aumento de 8%, a diferença, em reais, entre os preços do sapato com cada aumento seria de

(A) R$ 7,60.

(B) R$ 6,65.

(C) R$ 7,65.

(D) R$ 5,80.

(E) R$ 14,25.

​RESOLUÇÃO: 

Seja P o preço inicial do sapato. Com o aumento de 15% ele foi para 109,25 reais, ou seja,

P x (1 + 15%) = 109,25

P x (1 ,15) = 109,25

P = 109,25 / 1,15

P = 10925 / 115

P = 95 reais

Com o aumento de 8%, ele iria para:

95 x (1 + 8%) =

95 x (1,08) =

102,6 reais

A diferença entre os dois preços é 109,25 – 102,6 = 6,65 reais.

Resposta: B

FCC – TRT/11 – 2017) Uma construtora convoca interessados em vagas de pedreiros e de carpinteiros. No dia de apresentação, das 191 pessoas que se interessaram, 113 disseram serem aptas para a função pedreiro e 144 disseram serem aptas para a função carpinteiro. A construtora contratou apenas as pessoas que se declararam aptas em apenas uma dessas funções. Agindo dessa maneira, o número de carpinteiros que a construtora contratou a mais do que o número de pedreiros foi igual a

(A) 19.

(B) 12.

(C) 65.

(D) 47.

(E) 31.

​RESOLUÇÃO: 

Se somarmos os que se declararam pedreiros com os que se declararam carpinteiros, temos 113 + 144 = 257. Veja que isto é MAIS do que 191, que é o total de pessoas.

 A diferença 257 – 191 = 66 é o número de pessoas aptas às duas profissões.

Assim, os que são APENAS pedreiros somam 113 – 66 = 47, e os que são APENAS carpinteiros são 78, de modo que a diferença é de 78 – 47 = 31.

Resposta: E

FCC – TRT/11 – 2017) Do seu salário líquido Raimundo separa 1/3 para pagar os gastos com moradia. Para alimentação Raimundo separa 2/5 do restante do dinheiro. Exatamente 1/3 do que restou, após os gastos com moradia e alimentação, Raimundo deposita em uma conta de investimento que, nesse mês, recebeu como depósito a quantia de R$ 780,00. Nesse mês, a quantia do salário que Raimundo separou para moradia e alimentação, somadas, foi igual a

(A) R$ 3.510,00.

(B) R$ 3.190,00.

(C) R$ 3.820,00.

(D) R$ 3.240,00.

(E) R$ 3.730,00.

​RESOLUÇÃO: 

Se o salário de Raimundo for R, ele gasta 1/3 com moradia, sobrando 2/3, ou seja, 2R/3. Para alimentação ele separa 2/5 deste restante, sobrando 3/5 deste restante, ou seja, 3/5 de 2R/3:

Sobra = (3/5) x (2R/3) = 2R/5

1/3 deste restante é depositado na poupança, ou seja, o depósito é de 1/3 x 2R/5 = 2R/15. Este valor foi de 780 reais, ou seja,

2R/15 = 780

R/15 = 390

R = 390 x 15

R = 5850 reais

A parte da moradia foi R/3 = 5850/3 = 1950 reais, e a parte da alimentação foi 2/5 x 2R/3 = 4R/15 = 4×5850/15 = 1560 reais, de modo que o gasto com essas duas despesas foi 1950 + 1560 = 3510 reais.

Resposta: A

FCC – TRT/11 – 2017) A frase que corresponde à negação lógica da afirmação: Se o número de docinhos encomendados não foi o suficiente, então a festa não acabou bem, é

(A) Se a festa acabou bem, então o número de docinhos encomendados foi o suficiente.

(B) O número de docinhos encomendados foi o suficiente e a festa não acabou bem.

(C) Se o número de docinhos encomendados foi o suficiente, então a festa acabou bem.

(D) O número de docinhos encomendados não foi o suficiente e a festa acabou bem.

(E) Se a festa não acabou bem, então o número de docinhos encomendados não foi o suficiente.

​RESOLUÇÃO: 

Temos a condicional p–>q onde:

p =o número de docinhos encomendados NÃO foi o suficiente

q = a festa NÃO acabou bem

A negação é dada por “p e ~q”, onde:

~q = a festa ACABOU bem

Assim, a negação é:

“O número de docinhos encomendados NÃO foi o suficiente E a festa ACABOU bem”

Resposta: D

FCC – TRT/11 – 2017) O início de uma corrida de percurso longo é realizado com 125 atletas. Após uma hora de prova, o atleta João Carlos ocupa a 39a posição dentre os 83 atletas que ainda participam da prova. Na segunda e última hora dessa corrida, aconteceram apenas quatro fatos, que são relatados a seguir na mesma ordem em que ocorreram:

1º) 18 atletas que estão à frente de João Carlos, desistem da prova;

2º) 7 atletas que até então estavam atrás de João Carlos, o ultrapassam;

3º) 13 atletas que estavam atrás de João Carlos desistem de prova;

4º) perto da chegada João Carlos ultrapassa 3 atletas.

O número de atletas que chegaram depois de João Carlos nessa prova superou o número daqueles que chegaram antes de João Carlos em

(A) 3.

(B) 8.

(C) 4.

(D) 7.

(E) 2.

​RESOLUÇÃO: 

Veja que João Carlos estava posição 39. Se 18 pessoas à frente dele desistem, ele vai para a posição 39 – 18 = 21, e o total de atletas cai para 65. Se mais 7 atletas ultrapassam João Carlos, ele vai para a posição 21 + 7 = 28. Se 13 atletas que estavam atrás dele desistem, a prova fica com 65 – 13 = 52 atletas. Se João passa mais 3 atletas próximo à chegada, ele vai para a posição 28 – 3 = 25. 

Portanto, ele ficou na posição 25. Isto mostra que haviam 24 atletas à frente dele, e 52 – 25 = 27 atletas atrás. 

O número de atletas que chegaram depois (57) superou o dos atletas que chegaram antes (24) em 27 – 24 = 3 unidades.

Resposta: A

 

Uma excelente preparação!

Saudações.