Raciocínio Lógico TRT SC – gabarito e prova resolvida – TODOS os cargos!

Caros alunos,

Vejam a seguir a minha resolução das questões de Raciocínio Lógico das provas do Tribunal Regional do Trabalho da 12ª Região (TRT/SC). Vou começar pela prova de Técnico Judiciário – Área Administrativa (TJAA).

As questões de Analista e Oficial de Justiça encontram-se após as de Técnico, ok? É só rolar a tela!!!

Para ver os enunciados completos das questões, baixem estas imagens gentilmente enviado por uma aluna minha que GABARITOU A PROVA!!!

PROVA TRT SC TJAA PARTE1

PARTE2

PARTE3

PARTE4

PARTE5

FGV – TRT/SC – 2017) A nova sala…

RESOLUÇÃO:

Veja que a pasta 2310 é a décima pasta da terceira gaveta do segundo arquivo.

Após esta, temos mais 2 pastas nesta gaveta: 2311 e 2312.

Temos ainda as seguintes gavetas que devem ser totalmente preenchidas, cada uma com 12 processos:

24, 25, 26, 31, 32, 33, 34, 35, 36, 41, 42, 43, 44, 45, 46, 51, 52, 53, 54, 55

Veja que são 20 gavetas, cada uma com 12 pastas, totalizando 20×12 = 240 pastas.

Na gaveta 56, temos que preencher as pastas 5601, 5602 e 5603, ou seja, 3 pastas.

Ao todo temos 2 + 240 + 3 = 245 pastas.

Resposta: A (245)

FGV – TRT/SC – 2017) O salão principal…

RESOLUÇÃO:

Temos a condicional p–>q no enunciado, onde:

p = tiver carteira de advogado

q = pode entrar

Esta proposição equivale a ~q–>~p, isto é:

Se não pode entrar, então não tem carteira de advogado

Assim, podemos dizer que se Pedro não pode entrar, então ele não tem carteira de advogado. Temos isso na letra C.

Veja que é possível que outras pessoas, além das que tem carteira de advogado, possam entrar. Isto faz com que frases como “se João entrou então tem carteira de advogado” não possam ser necessariamente concluídas a partir do enunciado.

Resposta: C (se Pedro não pode entrar, então ele não tem carteira de advogado)

FGV – TRT/SC – 2017) Em um tribunal…

RESOLUÇÃO:

A frase do enunciado pode ser reescrita como a condicional:

“Se o processo tem capa cinza, então ele não vai para o arquivo”

Esta condicional p–>q equivale à condicional ~q–>~p, ou seja:

“Se o processo vai para o arquivo, então ele NÃO tem capa cinza”

Como só existem processos de capa azul ou cinza, a frase acima equivale a dizer:

“Se o processo vai para o arquivo, então ele tem capa azul”

Temos essa informação na alternativa:

“todo processo que vai para o arquivo tem capa azul”.

Resposta: B (todo processo que vai para o arquivo tem capa azul)

FGV – TRT/SC – 2017) No mês de julho…

RESOLUÇÃO:

Partindo de 17h31min, Temos 29 minutos para chegar até 18h. Temos mais 6 horas para chegar às 24h, e mais 7h e 5 minutos para chegar até o horário de 07h05min.

Assim, a noite teve:

29min + 6h + 7h + 5min = 13h + 34min

Resposta: D (13h34min)

FGV – TRT/SC – 2017) Todas as pessoas…

RESOLUÇÃO:

Vamos julgar cada alternativa:

• todos os que conhecem Bianca gostam dela

Falso, pois parte das pessoas não gostam de Bianca (como diz a frase “algumas pessoas que conhecem Bianca não gostam dela).

• ninguém gosta de Bianca

Falso, pois o próprio enunciado fala de pessoas que gostam de Bianca.

• alguns que conhecem Bianca não conhecem Bernardo

Verdade, pois existem pessoas que conhecem Bianca e não gostam dela. Se essas pessoas também conhecessem Bernardo,elas deveriam gostar de Bianca (pois quem conhece os dois gosta de Bianca, como disse o enunciado).

• quem conhece Bernardo gosta de Bianca

Falso. Sabemos que quem conhece os DOIS realmente gosta de Bianca. Mas é possível existir pessoas que conhecem apenas Bernardo, assim essas pessoas não necessariamente gostam de Bianca.

• só quem conhece Bernardo e Bianca conhece Bianca

Falso, pois vimos que existem pessoas que conhecem Bianca e não gostam dela. Essas pessoas não conhecem Bernardo, afinal se o conhecessem também, gostariam de Bianca.

Resposta: C (alguns que conhecem Bianca não conhecem Bernardo)

FGV – TRT/SC – 2017) Os advogados Miguel e Lucas…

RESOLUÇÃO:

Lucas disse que a frase de Miguel é falsa. Se essa frase é falsa, a sua NEGAÇÃO é verdadeira.

A frase de Miguel é uma condicional p–>q, e sua negação é dada por “p e não-q”, ou seja:

“Esse processo é de danos morais E NÃO tem 100 páginas ou mais”

Outra forma de dizer isso é:

“Esse processo é de danos morais E tem MENOS DE 100 páginas”

Resposta: E (esse processo é de danos morais e tem menos de 100 páginas)

FGV – TRT/SC – 2017) Alguns consideram que …

RESOLUÇÃO:

Dividindo 90 dias por 7, temos o resultado 12 e o resto 6. Isto significa que 90 dias correspondem a 12 semanas completas e mais 6 dias.

Como 23 de março foi sábado, o dia seguinte foi um domingo. A partir daí temos 12 semanas completas, todas começando em um domingo e terminando no sábado seguinte, e mais seis dias: domingo, segunda, terça, quarta, quinta, SEXTA.

Portanto, o dia 21 de junho é SEXTA.

Resposta: E (sexta-feira)

FGV – TRT/SC – 2017) Davi, João…

RESOLUÇÃO:

Como Davi é mais jovem que Gabriel e Pedro, e Gabriel é mais velho que Pedro, temos:

… Gabriel … Pedro … Davi …

Veja que estou colocando as pessoas em ordem decrescente de idade, ou seja, à esquerda temos os mais velhos e à direita os mais novos. As reticências indicam que podemos ter pessoas entre eles.

Temos que posicionar ainda João e Artur. Veja que alguém precisa ser mais velho que Gabriel (ele não é o mais velho de todos), e alguém precisa ser mais jovem que Davi (ele não é o mais jovem).

Como Artur é mais jovem que Pedro, ele não pode ser o mais velho de todos. O mais velho de todos é, portanto, João. Já o mais novo precisa ser Artur, para evitar que Davi seja o último. Ficamos com:

João – Gabriel – Pedro – Davi – Artur

Como a fila é em ordem crescente de idade, Artur será o primeiro e João o último.

Resposta: E (João está no último lugar da fila)

FGV – TRT/SC – 2017) Considere verdadeiras…

RESOLUÇÃO:

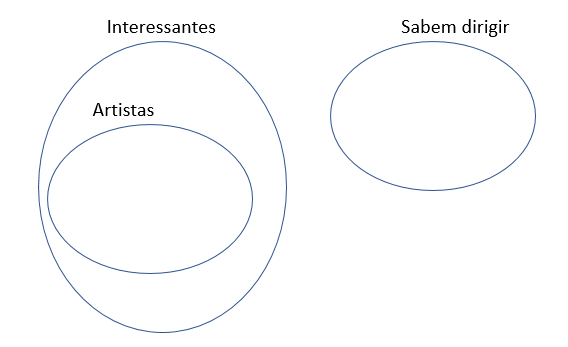
Imagine os conjuntos dos artistas, dos interessantes e dos que sabem dirigir.

Como todos os artistas são interessantes, eles estão totalmente dentro do conjunto dos interessantes. Como os interessantes não sabem dirigir, o conjunto das pessoas que dirigem está totalmente fora do conjunto dos interessantes.

Temos algo assim:

O esquema deixa claro que nenhum artista sabe dirigir.

Resposta: E (nenhum artista sabe dirigir)

FGV – TRT/SC – 2017) Um funcionário do tribunal…

RESOLUÇÃO:

Se dividíssemos igualmente os 80 processos entre os 7 advogados, teríamos o resultado 11 e o resto 3. A partir daí, podemos imaginar como foi feita a divisão.

Suponha que distribuímos 12 processos para cada um dos seis advogados que receberam a mesma quantidade. Com isso, teríamos distribuído 6×12 = 72, restando 80 – 72 = 8 para o último advogado.

Agora imagine que distribuímos 13 processos para cada um dos seis advogados que receberam a mesma quantidade. Com isso, teríamos distribuído 6×13 = 78 processos, restando 80 – 78 = 2 para o último. Veja que este caso não pode ser aceito, pois foi dito que o último recebeu MAIS de 5 processos.

Concluímos que o único caso possível é aquele em que distribuímos 12 processos para cada, e o último recebe 8.

Resposta: B (8)

QUESTÕES DE ANALISTA JUDICIÁRIO E OFICIAL DE JUSTIÇA 

FGV – TRT/SC – 2017) Sabe-se que são verdadeiras…

RESOLUÇÃO:

Podemos esquematizar assim:

Z–>~X

~Z–>Y

A primeira frase pode ser transformada na equivalente: X–>~Z. Assim, ficamos com:

X–>~Z

~Z–>Y

Juntando as duas:

X–>~Z–>Y

Ou seja,

X–>Y

Podemos dizer que X é SUFICIENTE para Y, e que Y é NECESSÁRIO para X.

Logo, o gabarito é:

“Y é necessário para X”

Resposta: E (Y é necessário para X)

FGV – TRT/SC – 2017) Se o dobro de x…

RESOLUÇÃO:

O dobro de X é igual ao triplo de Y:

2X = 3Y

Dividindo ambos os lados por 2, temos:

X = 3Y/2

Dividindo ambos os lados por 3, temos:

X/3 = Y/2

Vemos que a terça parte de X (X/3) corresponde à metade de Y.

Resposta: A (metade de Y)

FGV – TRT/SC – 2017) Uma gaveta A…

RESOLUÇÃO:

Colocando 3 canetas de A em B, ficamos com:

A: 4 vermelhas

B: 3 vermelhas e 7 azuis

Agora vamos tirar 4 canetas de B (que podem ser 4 azuis, 3 vermelhas e 1 azul, 2 vermelhas e 2 azuis, ou 1 vermelha e 3 azuis) e passar para A.

Analisando as opções de resposta:

• só ficaram canetas azuis na gaveta B

Falso, é possível que canetas vermelhas permaneçam em B.

• só ficaram canetas vermelhas na gaveta A

Falso, é possível que canetas azuis tenham vindo para A.

• há pelo menos uma caneta vermelha na gaveta B

Falso, é possível que B tenha novamente apenas canetas azuis, caso as 3 vermelhas tenham sido levadas de volta para A.

• há pelo menos uma caneta azul na gaveta A

Verdadeiro. Como serão tiradas 4 canetas de B, e lá só temos 3 vermelhas, certamente pelo menos 1 caneta azul será levada de B para A.

• há mais canetas azuis na gaveta B do que canetas vermelhas na gaveta A

Falso. É possível, por exemplo, levarmos 3 canetas vermelhas e 1 azul de B para A, e assim ficamos com:

A: 7 vermelhas e 1 azul

B: 6 azuis

Veja que, neste caso, há menos canetas azuis em B do que vermelhas em A.

Resposta: D (há pelo menos uma caneta azul na gaveta A)

FGV – TRT/SC – 2017) Considere como verdadeiras…

RESOLUÇÃO:

Como Beatriz não é brasileira, o trecho “Beatriz é brasileira” da segunda premissa é F. Assim, o trecho Denise não é espanhola precisa ser V. Com isso, o trecho “Denise é espanhola” da primeira premissa é F, obrigando o trecho “Jorge é francês” a ser F também, de modo que Jorge não é francês.

Considerando as conclusões sublinhadas, podemos marcar a alternativa:

“Se Jorge não é francês, então Denise não é espanhola”, que é uma condicional V–>V, ou seja, verdadeira.

Resposta: E (Se Jorge não é francês, então Denise não é espanhola)

FGV – TRT/SC – 2017) João é mais baixo…

RESOLUÇÃO:

Colocando as pessoas em ordem decrescente de altura, e sabendo que João é mais baixo do que Ana, temos:

… Ana … João …

Pedro não é mais baixo que Ana:

… Pedro … Ana … João …

Como Denise não é mais alta do que João:

Pedro – Ana – João – Denise

Com isso, podemos concluir que João é mais baixo do que Pedro.

Obs.: a rigor, seria preciso considerar que Pedro e Ana podem ter a mesma altura, e que João e Denise também podem ter a mesma altura. Mas isso não altera o gabarito correto.

Resposta: D (João é mais baixo do que Pedro)

FGV – TRT/SC – 2017) Sabe-se que:

• Se X é vermelho…

RESOLUÇÃO:

Esquematizando as proposições:

X –> ~Y

~X –> ~Z

Y –> Z

Vejamos uma solução bem rápida, e depois a “solução tradicional” pelo método do chute.

Solução Rápida:

Podemos substituir a primeira pela equivalente Y–>~X. Também podemos substituir a terceira pela equivalente ~Z–>~Y. Assim, temos:

Y–>~X

~X –> ~Z

~Z–>~Y

Veja que podemos juntar as 3, ficando:

Y–>~X–>~Z–>~Y

Ou seja,

Y –> ~Y

Para esta proposição ser verdadeira, é preciso que ~Y seja V e que Y seja F. Caso contrário (ou seja, se Y for V), essa proposição será falsa. Logo, podemos concluir que ~Y é V, ou melhor, concluir que Y é F. Isto é, Y não é verde.

Solução tradicional (método do chute):

Suponha que X é vermelho, ou seja, X é V. Assim, é preciso que ~Y seja V também para tornar a primeira premissa verdadeira. Isso já torna a segunda premissa verdadeira (pois ~X é F) e a terceira também (pois Y é F). Ou seja, considerando que X é vermelho, é possível tornar todas as premissas verdadeiras.

Suponha agora que X não é vermelho, ou seja, X é F. Isso já torna a primeira premissa verdadeira. Para a segunda ser verdadeira, precisamos que ~Z seja V. Com isso, Z é F, de modo que Y precisa ser F também para deixar a proposição verdadeira. Ou seja, considerando que X não é vermelho, também é possível deixar todas as premissas verdadeiras.

Note que nada podemos concluir a respeito de X: sendo verdadeiro ou falso, é possível deixar todas as premissas verdadeiras.

Vamos para a análise de Y.

Supondo que Y é V, a terceira premissa indica que Z deve ser V também. Assim, ~Z é F, de modo que na segunda premissa ~X deve ser F também. Com isso, X é V, e como ~Y é F, a primeira premissa fica V–>F, o que a torna falsa. Logo, Y não pode ser V, pois se Y fosse V seria impossível tornar todas as premissas verdadeiras.

Caso Y seja F, a terceira premissa já seria verdadeira, e a primeira também (pois ~Y seria V). Seria ainda possível encontrar uma combinação de valores lógicos que tornasse a segunda premissa verdadeira. Portanto, podemos concluir que Y é F (ou melhor, Y não é verde), pois se Y fosse verdadeiro alguma premissa ficaria falsa.

Analisando Z: supondo que Z é verdadeiro, a terceira premissa fica verdadeira. Para deixar a segunda verdadeira, precisamos que ~X seja F. Com isso, para a primeira ser verdadeira, precisamos que ~Y seja V. Assim, é possível deixar todas as premissas verdadeiras quando consideramos que Z é V.

Considerando agora que Z é F, a segunda premissa fica verdadeira. Para a terceira ser verdadeira, Y deve ser F também. Com isso, a primeira premissa já fica verdadeira.

Logo, é possível deixar todas as premissas verdadeiras quando Z é F.

Repare que não é possível concluir nada sobre Z, afinal é possível deixar todas as premissas verdadeiras quando Z é V e também quando Z é F.

A única conclusão possível é sobre Y, que deve ser F (Y não é verde).

Resposta: D (Y não é verde)

FGV – TRT/SC – 2017) A negação lógica…

RESOLUÇÃO:

Temos a condicional (A e B) –>C, em que:

A = eu como

B = não corro

C = engordo

A sua negação é:

(A e B) E ~C

Ou seja,

“Eu como e não corro E não engordo”

Resposta: B (Eu como e não corro e não engordo)

FGV – TRT/SC – 2017) Considere a sentença…

RESOLUÇÃO:

Para a sentença não ser falsa, não pode acontecer de a primeira parte ser verdadeira (x ser par e y ser maior que x) e, ao mesmo tempo, a segunda parte ser falsa (y ser par).

Vejamos os casos onde a proposição fica falsa:

a) se x for par (2 ou 4) e y for maior do que x (só podendo ser 3 ou 5), então claramente não tem como y ser par. Aqui é impossível deixar a proposição falsa. Este é o gabarito.

Vamos analisar a alternativa B para ficar mais claro. Neste caso podemos ter x = 2 e y = 4. Veja que obedecemos a primeira parte (x é par e y é maior que x), mas não a segunda (pois y é par). Isso torna a sentença falsa.

A mesma lógica vale para as demais alternativas.

Resposta: A (A = {2,3,4} e B = {2,3,5})

FGV – TRT/SC – 2017) Considere a sentenças: “Se Pedro…

RESOLUÇÃO:

Temos a condicional (A e B)–>C, onde:

A = Pedro é torcedor do Avaí

B = Marcela não é torcedora do Figueirense

C = Joana é torcedora da Chapecoense

Esta condicional equivale a:

~(A e B) ou C

Isto é,

(~A ou ~B) ou C

Escrevendo esta:

“Pedro não é torcedor do Avaí ou Marcela é torcedora do Figueirense ou Joana é torcedora da Chapecoense”

Temos isso na alternativa C.

Resposta: C (Pedro não é torcedor do Avaí ou Marcela é torcedora do Figueirense ou Joana é torcedora da Chapecoense)

FGV – TRT/SC – 2017) Em uma caixa só…

RESOLUÇÃO:

Como não é verdade que todas as bolas são pretas, podemos afirmar que alguma bola / pelo menos uma bola NÃO é preta. Ou seja, alguma bola é branca (pois só temos essas duas cores). Assim, o gabarito é:

‘Há pelo menos uma bola  branca na caixa”

Resposta: D (há pelo menos uma bola branca na caixa)

Espero que vocês tenham ido bem!

Saudações.