Raciocínio Lógico TRT 20 FCC – provas resolvidas
Caros alunos,
Vejam abaixo minhas resoluções das questões de Raciocínio Lógico cobradas no concurso do TRT 20 (SE) neste último final de semana. Espero que você tenha ido tão bem quanto esta minha aluna:

TÉCNICO JUDICIÁRIO
FCC – TRT/20 – 2016) Juliana consegue arquivar 16 pastas de documentos em uma hora e vinte minutos. Mantendo esse mesmo padrão, em duas horas e quarenta e cinco minutos Juliana conseguirá arquivar um número de pastas de documentos igual a (A) 32. (B) 40. (C) 35. (D) 38. (E) 33.
RESOLUÇÃO:
Veja que 1 hora e 20 minutos corresponde a 60 + 20 = 80 minutos. Já 2 horas e 45 minutos correspondem a 2×60 + 45 = 120 + 45 = 165 minutos. Podemos montar a regra de três:
16 pastas ——————– 80 minutos
N pastas ——————— 165 minutos
16 x 165 = N x 80
2 x 165 = N x 10
330 = N x 10
N = 33 pastas
Resposta: E
FCC – TRT/20 – 2016) Manoel e Dolores precisavam classificar um grande número de processos. Manoel começou antes do que Dolores e ao final do dia havia classificado 3/8 do total de processos. Dolores trabalhou mais rápido do que Manoel e ao final do dia havia classificado 1/3 de processos a mais do que aqueles que Manoel havia classificado. Após esse dia de trabalho de Manoel e Dolores, é correto afirmar que
(A) ainda faltam 1/4 dos processos para serem classificados.
(B) eles terminaram a tarefa.
(C) ainda faltam 1/8 dos processos para serem classificados.
(D) eles classificaram 17/24 dos processos.
(E) eles classificaram apenas metade dos processos.
RESOLUÇÃO:
Veja que 1/3 do que Manoel fez é:
1/3 de 3/8 =
1/3 x 3/8 =
1/8
Portanto, Dolores fez 3/8 + 1/8 = 4/8. Somando isso com o que foi feito por Manoel, ficamos com 4/8 + 3/8 = 7/8. Deste modo, ficou faltando apenas 1/8 dos processos.
Resposta: C
FCC – TRT/20 – 2016) Em um dia de atendimento externo, João atendeu 56 pessoas. No dia seguinte, João atendeu 25% a mais do número de pessoas que havia atendido no dia anterior. No terceiro dia, João novamente aumentou o número de atendimentos em 30% do número de atendimentos do dia anterior. O número de atendimentos realizados por João, nesses três dias, foi igual a (A) 195. (B) 217. (C) 161. (D) 184. (E) 111.
RESOLUÇÃO:
No segundo dia João atendeu 25% a mais, ou seja:
Segundo dia = 56 x (1 + 25%) = 56×1 + 56x(1/4) = 56 + 14 = 70 pessoas
No terceiro dia João atendeu 30% a mais que no segundo dia:
Terceiro dia = 70 x (1 + 30%) = 70×1 + 70×0,3 = 70 + 21 = 91 pessoas
Deste modo, nos três dias temos 56 + 70 + 91 = 217 pessoas.
Resposta: B
FCC – TRT/20 – 2016) Considere que todo técnico sabe digitar. Alguns desses técnicos sabem atender ao público externo e outros desses técnicos não sabem atender ao público externo. A partir dessas afirmações é correto concluir que
(A) os técnicos que sabem atender ao público externo não sabem digitar.
(B) os técnicos que não sabem atender ao público externo não sabem digitar.
(C) qualquer pessoa que sabe digitar também sabe atender ao público externo.
(D) os técnicos que não sabem atender ao público externo sabem digitar.
(E) os técnicos que sabem digitar não atendem ao público externo.
RESOLUÇÃO:
Considere três conjuntos:
- Técnicos
- Pessoas que sabem digitar
- Pessoas que sabem atender
Como todo técnico sabe digitar:
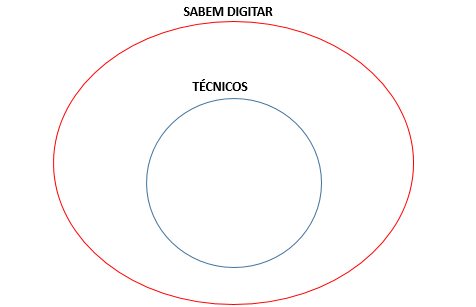
E como alguns técnicos sabem atender e outros não sabem, temos:
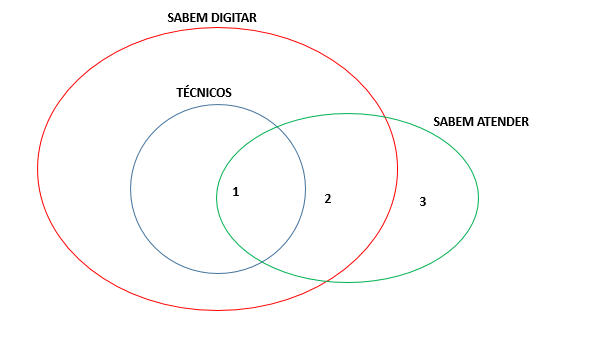
Veja que marquei 3 regiões no diagrama. Na região 1 temos certeza que há alguém (pois existem técnicos que sabem atender). Na outra parte do conjunto dos técnicos (fora a região 1) também sabemos que existem pessoas (pois existem técnicos que não sabem atender).
Na região 2 ou 3 não sabemos se existe ou não existem pessoas.
Com isso, podemos julgar as afirmações:
(A) os técnicos que sabem atender ao público externo não sabem digitar. –> ERRADO, pois todos os técnicos sabem digitar.
(B) os técnicos que não sabem atender ao público externo não sabem digitar.–> ERRADO, todo técnico sabe digitar.
(C) qualquer pessoa que sabe digitar também sabe atender ao público externo. –> ERRADO, há regiões do conjunto vermelho (pessoas que sabem digitar) que não fazem parte do conjunto verde (pessoas que sabem atender).
(D) os técnicos que não sabem atender ao público externo sabem digitar. –> CORRETO, pois TODOS os técnicos sabem digitar (inclusive os que não sabem atender).
(E) os técnicos que sabem digitar não atendem ao público externo.–> ERRADO, pois existem técnicos que sabem digitar e atender (na região 1).
Resposta: D
FCC – TRT/20 – 2016) A sequência de números 1; 13; 1; 2; 13; 1; 2; 3; 13; 1; 2; . . ., foi criada com um padrão e possui vinte termos. A soma dos termos: 20o , 15o e 13o é um número (A) múltiplo de 5. (B) múltiplo de 9. (C) divisor de 2. (D) múltiplo de 8. (E) divisor de 6.
RESOLUÇÃO:
Veja a sequência desta forma:
1; 13; 1; 2; 13; 1; 2; 3; 13; 1; 2; . . .
Veja que os números “13” em vermelho servem apenas como separadores. Entre eles temos a sequência:
- 1
- 1, 2
- 1, 2, 3
Dando continuidade a esta lógica, teremos:
1; 13; 1; 2; 13; 1; 2; 3; 13; 1; 2; 3; 4; 13; 1; 2; 3; 4; 5; 13
Deixei sublinhados o 13o, 15o e o 20o termos, cuja soma é 4 + 1 + 13 = 18. Este número é múltiplo de 9.
Resposta: B
ANALISTA JUDICIÁRIO
FCC – TRT/20 – 2016) Uma situação judicial exige que o valor de R$ 810.000,00 seja repartido em três partes de forma que a segunda seja igual ao dobro da primeira e a terça parte da terceira. Feita a repartição dessa maneira, a diferença entre a maior e a menor das três partes foi, em reais, de (A) 480.000,00. (B) 420.000,00. (C) 460.000,00. (D) 380.000,00. (E) 450.000,00.
RESOLUÇÃO:
Sejam P, S e T a primeira, segunda e terceira partes. Como a segunda é o dobro da primeira:
S = 2P
E como a segunda é a terça parte da terceira:
S = T/3
Desta última equação podemos escrever que T = 3S. E, da primeira equação, podemos escrever que P = S/2. Somando as três partes, temos 810.000, ou seja:
P + S + T = 810.000
S/2 + S + 3S = 810.000
S/2 + 4S = 810.000
9S/2 = 810.000
S/2 = 90.000
S = 180.000
Assim,
P = S/2 = 180.000 / 2 = 90.000
T = 3S = 3 x 180.000 = 540.000
A diferença entre a maior e a menor partes é:
540.000 – 90.000 = 450.000
Resposta: E
FCC – TRT/20 – 2016) Do ponto de vista da lógica, a proposição “se tem OAB, então é advogado” é equivalente à (A) tem OAB ou é advogado. (B) se não tem OAB, então não é advogado. (C) se não é advogado, então não tem OAB. (D) é advogado e não tem OAB. (E) se é advogado, então tem OAB.
RESOLUÇÃO:
Temos a condicional p–>q onde:
p = tem OAB
q = é advogado
Ela tem duas equivalências “manjadas”:
~q–>~p: “Se NÃO é advogado, então NÃO tem OAB”
~p ou q: “NÃO tem OAB OU é advogado”
Veja que, na alternativa C, temos uma dessas equivalências “manjadas”.
Resposta: C
FCC – TRT/20 – 2016) Marina, Kátia, Carolina e Joana se sentam em uma mesa hexagonal (seis assentos), conforme indica a figura abaixo.
Sabe-se que Carolina se senta imediatamente à direita de Marina e em frente à Kátia; e que Joana não se senta em frente a um lugar vazio. Dessa forma, é correto afirmar que, necessariamente, (A) Kátia se senta imediatamente ao lado de dois lugares vazios. (B) Joana se senta imediatamente ao lado de Kátia. (C) Marina se senta em frente à Kátia. (D) Carolina se senta imediatamente ao lado de dois lugares vazios. (E) Carolina está tão distante de Kátia na mesa quanto está de Marina.
RESOLUÇÃO:
Veja abaixo a mesa, onde marquei os 6 lugares com letras:
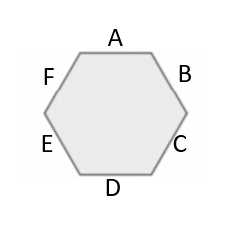
Suponha que Marina se senta no lugar D. Isto significa que Carolina se senta no lugar C, ou seja, à sua direita. E, como Kátia está em frente à Carolina, então Kátia está no lugar F. Até aqui temos:
Marina –> D
Carolina –> C
Kátia –> F
Continuando, veja que Joana não se senta em frente a um lugar vazio. Note que restam os lugares A, B e E para Joana. Como B e E estão vazios, e são um de frente para o outro, então Joana só pode se sentar em A.
Desta forma, repare que Joana se senta de frente à Marina. Mais do que isso, Joana se senta ao lado de Kátia (assentos A e F, respectivamente).
Veja que eu optei por assumir que Marina se sentou no lugar D para começar minha resolução. Você podia ter começado de forma diferente, assumindo que ela se sentou em outro lugar. Bastava manter a coerência no restante da resolução e você acertaria também.
Resposta: B
FCC – TRT/20 – 2016) Uma entidade assistencial pretende montar kits com vestimentas de inverno para distribuir em creches da cidade. Para a montagem dos kits, a entidade dispõe de 60 cobertores idênticos, 72 casacos idênticos e 108 calças idênticas. Se todos os kits são iguais e se todas as 240 vestimentas são utilizadas nos kits, o número máximo de kits que a entidade conseguirá montar é igual a (A) 24. (B) 180. (C) 60. (D) 12. (E) 6.
RESOLUÇÃO:
Precisamos achar um mesmo número que seja capaz de dividir os 60 cobertores, os 72 casacos e as 108 calças sem deixar resto. Estamos falando de um divisor comum desses números. Como queremos o maior número possível de kits, devemos buscar o MÁXIMO divisor comum entre eles. Fazemos isso assim:
DIVISOR 60 72 108
2 30 36 54
2 15 18 27
3 5 6 9
Como não há mais nenhum fator primo que divide 5, 6 e 9 simultaneamente, podemos parar por aqui. O MDC é 2x2x3 = 12. Este é o total de kits.
Resposta: D
FCC – TRT/20 – 2016) Um comerciante resolveu incrementar as vendas em sua loja e anunciou liquidação de todos os produtos com desconto de 30% sobre o preço das etiquetas. Ocorre que, no dia anterior à liquidação, o comerciante havia remarcado os preços das etiquetas para cima de forma que o desconto verdadeiro, durante a liquidação, fosse de 16% sobre o preço anterior ao aumento com a remarcação. Sendo assim, o aumento do preço feito na remarcação das etiquetas no dia anterior à liquidação foi de (A) 24%. (B) 20%. (C) 21%. (D) 32%. (E) 34%
RESOLUÇÃO:
Suponha que um produto custava 100 reais. Ele foi aumentado em p%, passando a custar 100 x (1+p%). Em seguida ele sofreu um desconto de 30%, passando a custar 100 x (1+p%) x (1 – 30%). Este preço final correspondeu a um desconto de 16% em relação ao preço inicial de 100 reais, ou seja, 84 reais. Isto é:
84 = 100 x (1+p%) x (1 – 30%)
84 = 100 x (1+p%) x 0,70
0,84 = (1+p%) x 0,70
0,84 / 0,70 = (1+p%)
84 / 70 = (1+p%)
12 / 10 = 1 + p%
1,2 = 1 + p%
p% = 0,2 = 20%
Resposta: B