Raciocínio Lógico PC/BA – prova resolvida e gabarito – investigador e escrivão

Caros alunos, vejam a seguir a minha resolução das provas de Raciocínio Lógico da PC/BA (Polícia Civil da Bahia) para os cargos de Investigador e Escrivão. Espero que vocês tenham se saído muito bem!

 

Raciocínio Lógico – INVESTIGADOR da PC/BA

VUNESP – PC/BA – 2018) Necessita-se identificar uma senha composta de cinco elementos distintos, sendo, cada elemento, um número de 1 a 9 ou uma das 26 letras do nosso alfabeto. Uma investigação revelou que o primeiro elemento é um número múltiplo de 3, o segundo elemento é uma vogal, o terceiro é um número par e os últimos dois elementos
são um número e uma letra, ou vice-versa. Com apenas essas informações, a probabilidade de se identificar essa senha, aleatoriamente, na primeira tentativa, é de 1 para
(A) 18080.
(B) 18560.
(C) 19040.
(D) 19520.
(E) 20000.

RESOLUÇÃO:

Para o primeiro elemento temos 3 possibilidades (3, 6 ou 9).

Para o segundo elemento temos 5 possibilidades (A, E, I, O, U).

Para o terceiro elemento, temos:

• 4 possibilidades (2, 4, 6, 8), caso o primeiro elemento NÃO seja 6;
• 3 possibilidades (2, 4, 8), caso o primeiro elemento seja 6.

Veja que já usamos 2 números, restando 7 possibilidades, e 1 letra, restando 25 possibilidades. Para os dois últimos dígitos, podemos ter letra-número, nesta ordem, num total de 25×7 possibilidades, ou número-letra, num total de 7×25 possibilidades. Ao todo temos, para os dois últimos dígitos, 2 x 25 x 7 = 350 possibilidades.

 

Assumindo que o primeiro elemento é o SEIS, temos 1 possibilidade para ele, 5 para o segundo, 3 para o terceiro e 350 para os dois últimos, totalizando 1 x 5 x 3 x 350 = 5.250 possibilidades.

Assumindo que o primeiro elemento NÃO é o seis, temos 2 possibilidades para ele, 5 para o segundo, 4 para o terceiro, e 350 para os dois últimos, totalizando 2 x 5 x 4 x 350 = 14.000 possibilidades.

Ao todo temos 14.000 + 5.250 = 19.250 possibilidades.

A chance de acertar, de primeira, é de 1 em 19.250.

Resposta: D (embora haja um erro de grafia, pois temos 19.520 na versão oficial da prova. Com isso, a questão deve ser ANULADA).

 

VUNESP – PC/BA – 2018) De um argumento válido com duas premissas, conclui-se corretamente que Alexandre não é casado com Carla. Uma das premissas desse argumento afirma como verdadeiro que Alexandre é casado com Carla se, e somente se, Maria é irmã de Carla. Sendo assim, uma segunda premissa verdadeira para esse argumento é
(A) Carla não é irmã de Maria.
(B) Alexandre é casado com Carla.
(C) Maria é irmã de Carla.
(D) Alexandre é irmão de Maria.
(E) Maria não é irmã de Alexandre.

RESOLUÇÃO:

A premissa “Alexandre é casado com Carla se, e somente se, Maria é irmã de Carla” é uma bicondicional p<->q, onde:

p = Alexandre é casado com Carla

q = Maria é irmã de Carla

Sabemos que p é falsa, pois Alexandre NÃO é casado com Carla.

Assim, q também precisa ser falsa, para manter a bicondicional verdadeira. Logo, Maria NÃO é irmã de Carla.

Veja que ficamos com o argumento:

Premissa1: Alexandre é casado com Carla se, e somente se, Maria é irmã de Carla

Premissa2: Carla não é irmã de Maria

Conclusão: Alexandre não é casado com Carla

Este realmente é um argumento válido.

Resposta: A (Carla não é irmã de Maria)

 

VUNESP – PC/BA – 2018) Considere a seguinte afirmação: Todo homem é bípede e mamífero.
A alternativa que apresenta uma negação lógica para essa afirmação é:
(A) Nenhum homem é bípede e mamífero.
(B) Nenhum homem é bípede ou mamífero.
(C) Existe homem que não é bípede ou não é mamífero.
(D) Existe homem que não é bípede e não é mamífero.
(E) Alguns homens são bípedes e mamíferos.

RESOLUÇÃO:

A questão nos afirma que todos os homens tem 2 características obrigatoriamente: são bípedes, e também são mamíferos. Para negar esta frase, ou seja, desmentir o seu autor, basta mostrarmos que existe algum contra-exemplo, isto é, um homem que NÃO seja bípede OU NÃO seja mamífero.

A negação seria algo como:

Existe homem que NÃO é bípede OU NÃO é mamífero.

Resposta: C (Existe homem que não é bípede ou não é mamífero)

 

Raciocínio Lógico – ESCRIVÃO da PC/BA

VUNESP – PC/BA – 2018) Considere verdadeiras as afirmações I e II e falsa a afirmação III a seguir.
I. Se Marcos é inocente, então Camila é culpada.
II. Se Orlando é culpado, então Bárbara é inocente.
III. Camila não é culpada ou Bárbara é inocente.
A alternativa que contém uma afirmação necessariamente verdadeira, com base nas afirmações apresentadas, é:
(A) Marcos é inocente.
(B) Orlando não é culpado.
(C) Marcos não é inocente e Orlando é culpado.
(D) Marcos é inocente e Orlando não é culpado.
(E) Marcos é inocente ou Orlando é culpado.

RESOLUÇÃO:

Como III é falsa, sabemos que ambas as informações são F, de modo que é verdade que:

Camila É culpada

Bárbara é culpada

 

Sabendo disso, podemos analisar as demais proposições. Veja que, em II, o segundo trecho é F, de modo que o primeiro deve ser F também, ou seja, Orlando NÃO é culpado. Veja que, em I, a segunda parte é verdadeira, de modo que a proposição já fica verdadeira, independentemente do que acontece com Marcos. Assim, nada podemos concluir sobre Marcos, mas temos certeza que Orlando não é culpado, o que permite marcar a letra B.

Resposta: B (Orlando não é culpado)

 

VUNESP – PC/BA – 2018) Paula leu os livros A e B, mas não leu o livro C. Sérgio leu os livros A e C, mas não o B. Antonio e Roberto não leram o livro A, mas leram os livros B e C. Somente Wilza leu os três livros. Se, em um grupo de leitores dos quais participam todos os citados, apenas existem os que leram os livros A, B ou C, sendo 12, 10 e 8 leitores, respectivamente, e somente os citados leram mais de um livro, então é correto afirmar que o número de pessoas nesse grupo é
(A) 20.
(B) 21.
(C) 22.
(D) 23.
(E) 24.

RESOLUÇÃO:

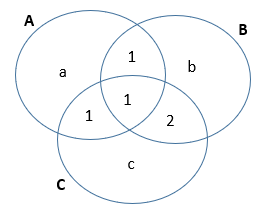
Podemos desenhar os conjuntos de leitores de cada um dos livros, já posicionando as pessoas que foram citadas:

Como temos 12 pessoas no grupo A, e já colocamos 3, faltam colocar a = 9 pessoas.

Como temos 10 pessoas no grupo B, e já colocamos 4, falta colocar b = 6 pessoas.

Como temos 8 pessoas no grupo C, e já colocamos 4, falta colocar c = 4 pessoas.

Ao todo temos:

a + 1 + 1 + 1 + b + 2 + c =

9 + 1 + 1 + 1 + 6 + 2 + 4 =

24 pessoas

Resposta: E (24)

 

VUNESP – PC/BA – 2018) Considere verdadeira a afirmação “se André é trabalhador, então Joana é estudante” e falsa a afirmação “André é trabalhador e Joana é estudante”.
Nessas condições, é correto afirmar que, necessariamente,
(A) André não é trabalhador.
(B) André é trabalhador.
(C) André e Joana são estudantes.
(D) André e Joana não são estudantes.
(E) Joana é estudante.

RESOLUÇÃO:

Se a segunda afirmação é falsa, pelo menos uma das proposições deve ser F. Imagine que “André é trabalhador” é F. Neste caso, isso já deixa a primeira proposição verdadeira.

Agora imagine que “André é trabalhador” é V. Neste caso, “Joana é estudante” deve ser F. Com isso, na primeira proposição, ficamos com V–>F, ou seja, uma proposição falsa.

Logo, fica evidente que a única solução de André que nos atende é André NÃO é trabalhador. Quanto à Joana, é possível atender ambas as proposições, seja ela estudante ou não.

Resposta: A (André não é trabalhador)