Raciocínio Lógico para AGU: o que é o Princípio da Regressão ou Reversão?

Oi, pessoal!

Tudo bem?

Saiu o edital do concurso da AGU!!!

Apareceu uma “novidade”no edital de Raciocínio Lógico: um tal de “Princípio da Regressão ou Reversão”.

Na verdade, nem é tão novidade assim, já que apareceu, por exemplo, no último concurso da AGU, também organizado pela IDECAN.

E aí, todos começam a perguntar: “o que é este tal princípio da regressão ou reversão??”

É muito simples, meu amigo: é apenas um método para resolver alguns problemas do primeiro grau, ou seja, problemas que recaem em equações do primeiro grau.

Mais especificamente, são problemas que podem ser resolvidos de “trás para frente”.

Vejamos um exemplo para aprender o tal princípio da reversão.

Guilherme tem uma certa quantia. Foi ao Shopping Center e ao entrar na primeira loja gastou a metade da quantia que tinha. Em seguida, foi à praça de alimentação e gastou 20 reais. Continuou o seu passeio e entrou em outra loja. Nesta segunda loja Guilherme gastou a metade do dinheiro que tinha sobrado. Em seguida, ele foi ao boliche e gastou 50 reais. Logo após, Guilherme foi a outra loja e gastou a metade do dinheiro que tinha sobrado. Finalmente, pagou R$ 8,00 de estacionamento. Neste momento, ele percebeu que ainda tinha 35 reais na carteira. Quantos reais Guilherme levou para o Shopping Center?

Resolução

A ideia é resolver o problema de trás para frente. Guilherme no final do problema tinha R$ 35,00. E o que ele fez por último? Pagou R$ 8,00 de estacionamento.

Isto significa que ele estava com 35 + 8 = R$ 43,00.

Antes de ficar com R$ 43,00, Guilherme tinha ido a uma loja e gastado a metade do dinheiro que possuía, ou seja, Guilherme tinha R$ 86,00.

Antes de ir a esta loja, Guilherme tinha gastado R$ 50,00 no boliche. Isto quer dizer que ele tinha R$ 86,00 + R$ 50,00 = R$ 136,00.

Antes do boliche, ele tinha gastado metade do dinheiro, ou seja, ele tinha 2×136 = 272 reais.

Antes desta loja, Guilherme tinha gastado R$ 20,00 na praça de alimentação. Portanto, ele tinha 272 + 20 = R$ 292,00.

E antes da praça de alimentação? Ele tinha gastado a metade do dinheiro na primeira loja. Isto significa que ele tinha 2×292 = 584 reais.

Fácil, não?

Vamos fazer um esquema gráfico para resolver o problema de uma maneira mais rápida.

Voltemos ao texto.

Guilherme tem uma certa quantia. Foi ao Shopping Center e ao entrar na primeira loja gastou a metade da quantia que tinha.

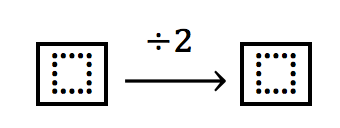
Em seguida, foi à praça de alimentação e gastou 20 reais.

Continuou o seu passeio e entrou em outra loja. Nesta segunda loja Guilherme gastou a metade do dinheiro que tinha sobrado.

Em seguida, ele foi ao boliche e gastou 50 reais.

Logo após, Guilherme foi a outra loja e gastou a metade do dinheiro que tinha sobrado.

Finalmente, pagou R$ 8,00 de estacionamento. Neste momento, ele percebeu que ainda tinha 35 reais na carteira.

Pronto. Basta agora que você volte trocando as operações. No lugar de subtrair, 8, some 8. No lugar de dividir por 2, multiplique por 2 e assim por diante.

Resposta: R$ 584,00

Vamos agora resolver um exemplo que caiu no último concurso da AGU, também organizado pela banca IDECAN.

(IDECAN 2014/AGU) Um pai deu a seu filho mais velho 1/5 das balinhas que possuía e chupou 3. Ao filho mais novo deu 1/3 das balinhas que sobraram mais 2 balinhas. Ao filho do meio, João, deu 1/6 das balinhas que sobraram, após a distribuição ao filho mais novo. Sabe-se que o pai ainda ficou com 30 balinhas. Quantas balinhas ele possuía inicialmente?

a) 55

b) 60

c) 75

d) 80

e) 100

Resolução

Basta utilizar o princípio da reversão e resolver de trás para frente.

Antes, vamos montar o nosso diagrama. Digamos que o pai possuía x balinhas inicialmente.

Se o pai deu 1/5 das balinhas para o filho mais velho, então ele ficou com 4/5 das balinhas.

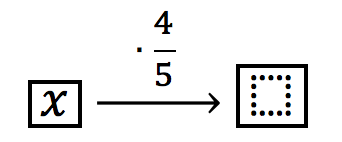
Em seguida, ele chupou 3 balas. Vamos diminuir 3 unidades do total que restou.

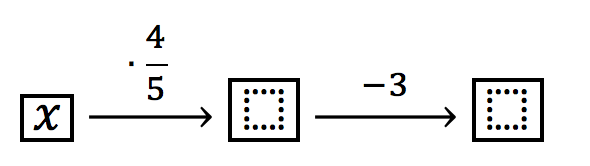
Ao filho mais novo, deu 1/3 das balinhas. Assim, sobraram 2/3 das balinhas.

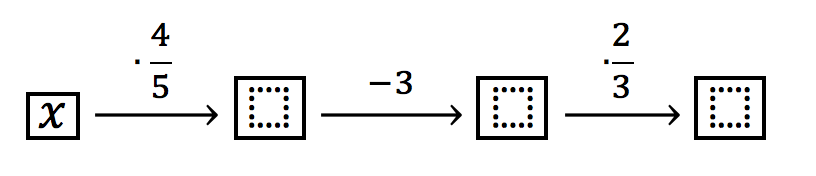
Em seguida, ele deu mais duas balinhas para o filho mais novo. Assim, vamos subtrair duas balinhas.

Finalmente, ele deu 1/6 do restante para o filho do meio. Assim, restaram 5/6 das balinhas, que corresponde a 30 balinhas.

Agora é só voltar realizando as operações inversas.

Se na ida nós multiplicamos por 5/6, na volta nós devemos dividir por 5/6, ou seja, devemos multiplicar por 6/5.

Vamos preencher o penúltimo quadradinho com 30 * 6/5 = 36.

Se na ida nós subtraímos 2, então na volta devemos adicionar 2. Vamos preencher o quadradinho anterior com 36 + 2 = 38.

Seguindo o mesmo raciocínio, o próximo quadradinho será preenchido por 38 * 3/2 = 57.

Agora temos 57 + 3 = 60.

Finalmente, temos 60 * 5/4 = 75.

Gabarito: C

Espero que tenham gostado!!

Um forte abraço e os espero no nosso curso de Raciocínio Lógico para o concurso da AGU. A aula demonstrativa já está disponível aqui.

Guilherme Neves

Instagram: @profguilhermeneves.