Questões de torneiras – Dica Estratégica de Matemática
Dica de Matemática – questões de torneiras
Olá, tudo bem? Vamos a mais uma dica estratégica, desta vez de Matemática? Falaremos sobre um tipo de questão bastante comum em provas de concurso. Estou falando daquelas questões que envolvem torneiras enchendo um tanque, nas quais você normalmente precisa calcular quanto tempo vai levar para o tanque ser enchido ou esvaziado (quando há um ralo). Se você já estuda para concursos há algum tempo, certamente já se deparou com uma ou mais questões deste tipo!

Para começarmos, leia o enunciado da questão abaixo, que ilustra bem este modelo de questão.
Abrindo-se uma torneira A, um reservatório ficará cheio em 3 horas. Abrindo-se a torneira B, encherá o reservatório em 2 horas. Em quanto tempo conseguiremos encher o reservatório caso as duas torneiras sejam abertas simultaneamente?
a) 1,2 hora
b) 2,5 horas
c) 1,3 hora
d) 1,4 hora
e) meia-hora
RESOLUÇÃO:
Veja que a torneira A é capaz de encher o tanque em 3 horas. Isto significa que, a cada hora, ela enche 1/3 do tanque. Afinal, enchendo 1/3 a cada hora, ao final de três horas teremos:
1/3 + 1/3 + 1/3 = 3/3 = 1
Ou seja, após 3 horas, de fato teremos enchido 1 tanque inteiro.
De forma análoga, como a torneira B enche o tanque em 2 horas, isto nos indica que a cada hora ela enche 1/2 do tanque.
Se abrirmos as duas torneiras, quanto será enchido a cada hora? Devemos somar as capacidades das duas torneiras, concorda? Ficaríamos com:
Enchimento a cada hora = 1/3 + 1/2 = 2/6 + 3/6 = 5/6
Portanto, em uma hora vamos encher 5/6 do tanque. Quantas horas (H) precisaremos para encher todo o tanque, ou seja, 1 tanque? Basta calcularmos:
(5/6) x H = 1
H = 1 x 6 / 5
H = 1,2 hora
Portanto, com as duas torneiras trabalhando juntas, vamos encher o tanque em 1,2 hora. Gabarito na alternativa A.
Repare um ponto interessante: ao ligar as duas torneiras simultaneamente, o tempo de enchimento deve ser MENOR do que o tempo de qualquer torneira separadamente. Como o valor da alternativa B é maior do que o da torneira B sozinha, podemos excluir de imediato a alternativa B, ficando com as demais para analisar. Este tipo de análise simples te ajuda a ter mais certeza de que você fez a resolução correta.
Resposta: A
Veja ainda mais essas 3 questões, para continuar a exercitar as questões que envolvem torneiras.
ESAF – ATA/MF – 2009) Existem duas torneiras para encher um tanque vazio. Se apenas a primeira torneira for aberta, ao máximo, o tanque encherá em 24 horas. Se apenas a segunda torneira for aberta, ao máximo, o tanque encherá em 48 horas. Se as duas torneiras forem abertas ao mesmo tempo, ao máximo, em quanto tempo o tanque encherá?
a) 12 horas
b) 16 horas
c) 20 horas
d) 24 horas
e) 30 horas
RESOLUÇÃO:
Observe que a primeira torneira enche o tanque em 24 horas, ou seja, a cada hora ela enche 1/24 do tanque. A segunda torneira enche, a cada hora, 1/48 do tanque, de modo que em 48 horas ela encheria completamente.
Juntas, a cada hora as duas torneiras enchem 1/24 + 1/48 = 2/48 + 1/48 = 3/48 = 1/16 do tanque.
Se a cada hora elas enchem 1/16 do tanque, após 16 horas elas terão enchido o tanque todo.
Resposta: B
CESGRANRIO – PETROBRAS – 2014) Certo reservatório continha 1.000 L de água quando foi aberta uma torneira de vazão constante. Cinquenta minutos mais tarde, sem que a torneira fosse fechada, um ralo foi destampado acidentalmente, permitindo o escoamento parcial da água. O Gráfico abaixo mostra a variação do volume de água dentro do reservatório, em função do tempo.
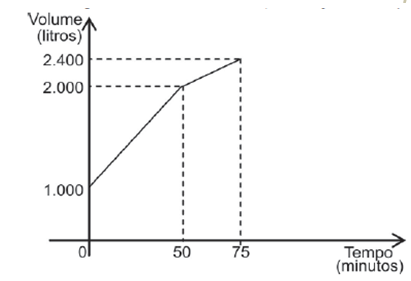
Qual era, em litros por minuto, a capacidade de escoamento do ralo?
(A) 20
(B) 12
(C) 6
(D) 4
(E) 2
RESOLUÇÃO:
Repare que a torneira encheu o reservatório em 1000 litros (de 1000 para 2000) em 50 minutos, ou seja, encheu 1000 / 50 = 20 litros por minuto.
Depois que o ralo foi aberto, a torneira encheu o reservatório em 400 litros (de 2000 para 2400) em 25 minutos, isto é, 400 / 25 = 16 litros por minuto.
A redução no ritmo de enchimento deve-se ao ralo, ou seja, este escoou 20 – 16 = 4 litros por minuto.
RESPOSTA: D
FCC – PREF. SÃO GONÇALO – 2011 Adaptada) Uma caixa d’água tem 2,4m3 de volume. A caixa está vazia, e uma torneira começa a enchê-la a uma razão constante de 15 litros por minuto. O tempo em que a torneira deve ficar aberta para que a caixa fique cheia é de:
a) 2 horas
b) 2 horas e 20 minutos
c) 2 horas e 40 minutos
d) 3 horas
e) 3 horas e 30 minutos
RESOLUÇÃO:
Veja que o volume da caixa está em metros cúbicos, enquanto a vazão (quantidade de água que jorra da torneira por minuto) está em litros. Devemos trabalhar com apenas 1 unidade. Neste caso, vamos transformar 2,4m3 em litros. Veja:
1m3——————————————1000 litros
2,4m3——————————————-X litros
1.X = 2,4 x 1000
X = 2400 m3
Agora sim, observe que a torneira é capaz de encher 15 litros em 1 minuto. Para calcular o tempo que ela leva para encher 2400 litros, usamos a regra de três abaixo:
15 litros —————————————- 1 minuto
2400 litros ———————————— T minutos
15.T = 2400.1
T = 2400/15
T = 160 minutos
Portanto, a torneira leva 160 minutos para encher a caixa. Entretanto, as respostas estão em horas e minutos. Sabemos que 60 minutos correspondem a 1 hora e 120 minutos a 2 horas. Veja que:
160 minutos =
120 minutos + 40 minutos =
2 horas + 40 minutos
Resposta: C
FCC – SABESP – 2014) Para encher de água um tanque, cuja capacidade é de 900 litros, foi providenciada uma torneira que, quando aberta, apresenta uma vazão de 800 mililitros de água por minuto. Com o tanque vazio, a torneira foi aberta às 20 horas e 30 minutos para enchê-lo. O término do enchimento do tanque se deu, no dia seguinte, às
(A) 15 horas e 15 minutos.
(B) 14 horas e 30 minutos.
(C) 16 horas e 55 minutos.
(D) 15 horas e 25 minutos.
(E) 17 horas e 15 minutos.
RESOLUÇÃO:
Observe que a cada minuto a torneira enche 800 mililitros, ou 0,8 litros. Para saber quanto tempo é necessário para encher 900 litros, podemos montar a seguinte regra de três:
0,8 litros ———- 1 minuto
900 litros ———- T minutos
0,8 x T = 900 x 1
T = 900 / 0,8
T = 9000 / 8
T = 4500 / 4
T = 2250 / 2
T = 1125 minutos
Lembrando que uma hora possui 60 minutos, podemos dividir 1125 minutos por 60, obtendo o resultado 18 e o resto 45. Isso significa que a torneira vai precisar de 18 horas e 45 minutos para encher o tanque. Contando 18 horas a partir das 20:30 do dia anterior, chegamos em 14:30h do dia seguinte. Com mais 45 minutos, chegamos às 15:15h, que é o momento onde termina o enchimento do tanque.
RESPOSTA: A