Binomial e Soluções inteiras e positivas

Olá, pessoal. Hoje vamos abordar dois temas que envolvem probabilidade para concursos: Teoria binomial e soluções inteiras e positivas. Esses assuntos fogem um pouco do “básico” de probabilidades e quando precisam ser aplicados, geram confusão nos alunos. Salienta-se que o assunto Teoria Binomial também é estudado em Estatística, na parte de distribuições contínuas.

Teoria Binomial

Conceito de binomial

Iniciando propriamente nosso assunto sobre probabilidade: teoria binomial e soluções inteiras e positivas, vamos começar com a Binomial. A teoria binomial se aplica quando precisamos eleger “sucesso” e “fracasso” em algum experimento. O termo “sucesso”, nobres, é só uma convenção que se usa para se dizer que esse evento é o que queremos. Já o “fracasso” é aquele evento que não queremos. Não necessariamente “sucesso” é algo bom na acepção da palavra. Por exemplo, queremos saber qual a probabilidade de quem come determinado alimento ter câncer. Esse é o “sucesso”, apesar de ser algo ruim no senso comum, ok??! Esse conceito, inclusive, foi cobrado na prova de estagiário do Tribunal de Contas do Estado de Pernambuco, ano 2022 – Especialidade Ciência atuariais:

Assim, modelo Binomial, descreve-se a variável aleatória X com um número de sucessos em n experimentos aleatórios independentes, onde cada experimento possui 2 resultados possíveis, sucesso ou fracasso, e onde a probabilidade de sucesso é igual a p e consequentemente a de fracassos é (1-p), já que o máximo que podemos ter de chances para 1(um) evento é 100% = 1. Segundo este modelo, a probabilidade de observar x sucessos, é dada por:

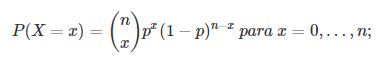
Traduzindo a fórmula, temos:

• N = total de eventos;
• x = número de sucessos;
• p = probabilidade de sucesso, e;
• (1-p) = probabilidade de fracasso.

Aplicação da teoria binomial

A questão clássica em concursos que abordam esse tema é a moeda lançada que queremos saber qual a probabilidade em N eventos de se ter cara(sucesso). Vamos supor que joguemos uma moeda 5(cinco) vezes. Queremos que haja 3(três) sucessos. Qual a probabilidade de isso acontecer?

Sabemos que uma moeda só tem “cara” e “coroa”. Assim, a probabilidade de sucesso é igual a probabilidade de fracassos = 1/2 ou 0,5. Com isso, já temos todos os dados. Vamos substituir na fórmula: P(X=3)=

No caso, lê-se combinação de 5, de 3 a 3. Assim, teremos 5!/(3!2!) x 0,5³x0,5²

Aí pessoal, é só conta de matemática básica. 5.4.3!/(3!x2x1)x0,5³x0,5² . Logo, a P(X=3) = 10×0,5³x0,5²

Soluções inteiras e positivas.

Conceito

Outro assunto das probabilidades que costuma “pegar” muitos candidatos é o caso do número de soluções inteiras e positivas de um determinado problema. Vamos usar um problema que consta no livro Fundamentos da Matemática Elementar, Samuel Hazzan, 5, editora Atual, pág. 54:

Um bar vende 3 tipos de refrigerantes: guaraná, soda e tônica. De quantas formas uma pessoa pode comprar 5 garrafas de refrigerantes? Seja: x o número de garrafas de guaraná; y o número de garrafas de soda e z o número de garrafas de tônica.

Aplicação para se encontrar Soluções inteiras e positivas.

Aqui, nobres, podemos achar a solução pela fórmula ou pelo raciocínio didático mais usado. Vamos começar pelo raciocínio. Temos que escolher 5 refrigerantes. Podemos, por exemplo, escolher 3 de guaraná, 1 de soda e 1 de tônica. São três partes, pois temos 3(três) incógnitas – x, y e z. Vamos representar as garrafas por pontos e a separação, por traços:

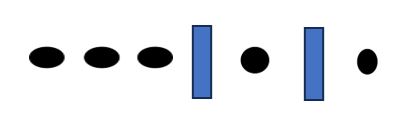
Temos, por oportuno, 5 pontos e 2 traços. Isso dá 7 símbolos, correto?

Dito isso, faremos uma permutação de 7!/5!2!, em que 5 são o nº de pontos e 2 são o número de barras. Logo, temos 7x6x5!/(5!x2x1). O 5! do numerador se anula com o 5! do denominador. Ficamos, então, com 42/2 = 21 formas de uma pessoa comprar 5 garrafas de refrigerantes.

Nesse assunto, ainda, é bom reforçar que o tema se aplica quando você precisa de soluções positivas(não é possível ter menos 2 garrafas no nosso exemplo) e inteiras(eu não quero meia garrafa de refrigerante). Portanto, fiquem atentos!.

Já a fórmula para esse tipo de questão, nobres, é a seguinte:

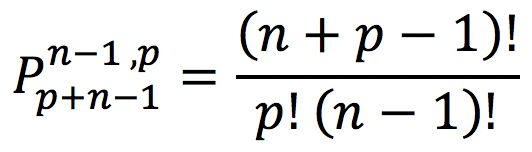
Em que n é o nº de incógnitas(no nosso exemplo, os tipos de refrigerantes); p é o nº de pontinhos(no nosso exemplo, o número de garrafas que queremos).

(3 + 5 -1)!/ 5!(3-1)! = 21

Questões sobre teoria binomial e soluções inteiras e positivas

Para vocês treinarem, deixamos abaixo questões, do nosso sistema de questões, que abordam os assuntos teoria binomial e soluções inteiras e positivas:

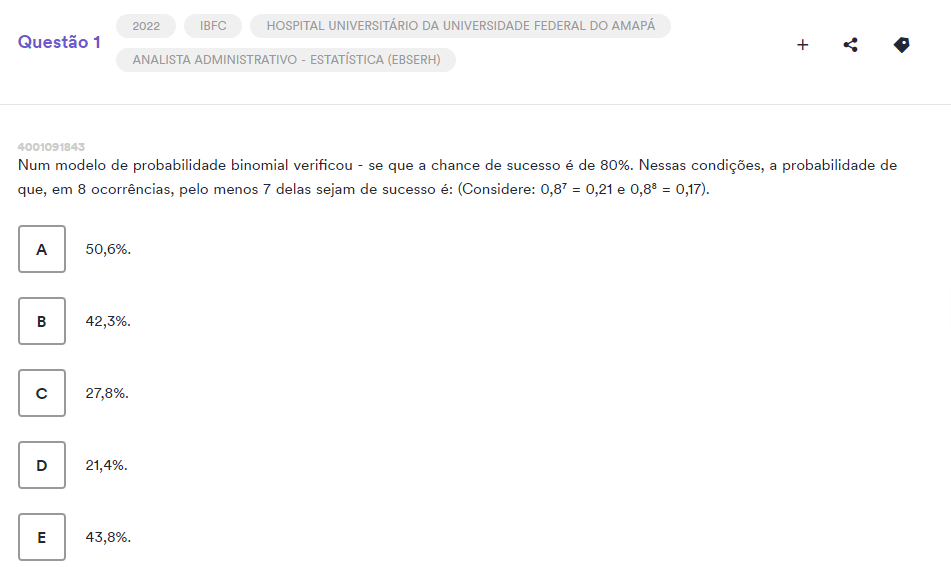
Solução: Aqui a questão já deixou clara que se trata de uma binomial. Vamos lá! Se a chance de sucesso é 80% ou 0.8, a de fracasso é 0,2, correto?!

Eu quero, NO MÍNIMO, 7 ocorrências de “sucesso”. Assim, posso ter 7 em 8 chances ou 8 em 8 chances. Então, termos que aplicar, nesse caso, a fórmula 2(duas) vezes:

7 sucessos:

P(X=7):

Usando os dados da questão:

P(X=7) = 8×0,21×0,2. Temos P(X=7) = 0,336

8 sucessos:

P(X=8):

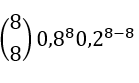
P(X=8) = 1×0,17×1

Obs.: Combinação de 8 para 8 vale 1(um), pessoal. Bem como todo número elevado a zero(no caso de 0.2) também vale 1.

Então: P(X=8) = 0,17

Somando-se P(7) + P(8) = 0,336 + 0,17 = 0,506 ou 50,6%(gabarito)

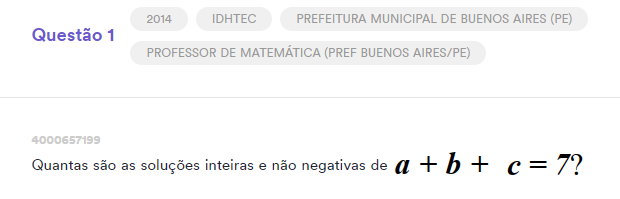
Solução: Aqui, pessoal, vamos usar o raciocínio didático. Dessa forma, iremos dividir o 7 em 3(três) partes já que são 3 incógnitas (a, b e c). Fazendo a didática dos pontos e barras, podemos sugerir a = 3(pontinhos), b=3(pontinhos) e c = 1(pontinho). Para separá-los precisaremos de 2 barras, certo?!

Logo, teremos Permutação(P) = 9!/7!x2!. Isso dá um valor de 36 soluções(gabarito).

Conclusão

Finalizamos aqui mais um artigo. Esperamos que seja útil na caminhada de vocês rumo à aprovação. Por fim, frisamos mais uma vez que o tema -Teoria binomial e Soluções inteiras e positivas – foge do básico de probabilidades e com certeza fará diferença na preparação.

Bons estudos!

Quer estar antenado aos próximos concursos previstos? Confira nossos artigos!

Concursos Abertos

Concursos 2024