Probabilidade para SEFAZ-RJ: Estatística

Olá, pessoal. Tudo certo? No artigo de hoje veremos o resumo sobre Probabilidade para SEFAZ-RJ, tema da Estatística.

O artigo será divido da seguinte forma:

• Conceitos Gerais
• Definição Clássica de Probabilidade
• Combinações de Eventos
• Probabilidade Condicional

Sem mais delongas, vamos lá!

Conceitos Gerais

Iniciemos o resumo sobre Probabilidade para SEFAZ-RJ, pela definição de Probabilidade.

A probabilidade é uma medida numérica que quantifica a chance de um evento ocorrer. 

Assim, a Teoria da Probabilidade é o ramo da Estatística que estuda experimentos aleatórios, cujos resultados são incertos.

O exemplo mais clássico é o lançamento de um dado. Qual a probabilidade de jogarmos um dado e cair o número 3? Simples, uma chance em 6 possíveis, logo 1/6 = 0,16666 = 16,66%

Embora os resultados sejam incertos, ao repetir esses experimentos várias vezes, é possível identificar um padrão.

Outras definições precisam ser conhecidas.

• Espaço Amostral: conjunto de todos os resultados possíveis, ou seja, o universo (U) de possibilidades – ex. para o dado U = {1, 2, 3, 4, 5, 6}
• Evento: subconjunto do Espaço Amostral – ex. a “coroa” em um lançamento de moeda.

Em termos de classificação, o evento pode ser simples (elementar), quando só um elemento; impossível, se o conjunto for vazio; e o evento certo, caso corresponda a todo o espaço amostral.

Fiquemos também com os axiomas da probabilidade.

• Não há probabilidade negativa
• A probabilidade associada a todos os eventos (Espaço Amostral) é sempre 100%.
• Se A e B são mutuamente excludentes então ????(???? ∪ ????) = ????(????) + ????(????)

Definição Clássica de Probabilidade

Com o conhecimento sobre espaço amostral e evento, podemos utilizar a Definição Clássica de Probabilidade.

Ou seja, a probabilidade será os casos favoráveis n(A), pelo total de número de casos n(U). Em outros termos, Evento / Espaço Amostral.

P = casos favoráveis / Casos totais

É importante entender que para a definição clássica de probabilidade, todos os elementos são igualmente prováveis.

Entretanto, podemos extrapolar para casos mais genéricos, mesmo que de probabilidades diferentes,

P = Quero / Tenho

Outra informação que deve ficar clara, mesmo que a probabilidade de um evento seja de “X” (ex. 20%), isso não significa que ele ocorrerá exatamente 20% das vezes.

Vamos retomar o exemplo do lançamento de dados. Já vimos que cada número tem 1/6 de probabilidade, então se jogarmos 6 vezes o dado, “cairá” obrigatoriamente o número 3, por exemplo? Sabemos que não.

Entretanto, se jogarmos o dado por “infinitas vezes”, se espera que a média de cada número seja 1/6.

Combinações de Eventos

Prosseguindo no resumo sobre Probabilidade para SEFAZ-RJ, vamos tratar sobre as hipóteses de Combinações de Eventos.

• Teorema da União: trata-se da união de dois eventos para formação de um novo

Vejamos um exemplo,

A = {1, 2, 3, 4}
B = {4, 5, 6}
A U B = {1, 2, 3, 4, 5, 6}

Entretanto, devemos ter atenção em casos de elementos duplicados. Atente-se que o “4” é contado apenso uma vez.

Ainda, quando não há intersecção, dizemos que os eventos são Mutuamente Excludentes.

C = {1, 2, 3}
D = {4, 5, 6}
C U D = {1, 2, 3, 4, 5, 6}

Memorize as fórmulas,

Atente-se no caso de união de 3 eventos.

P(????∪????∪C) = ????(????) + ????(????) + ????(C) − ????(????∩????) − ????(B∩C) − ????(A∩C) + ????(A∩BC)

• Teorema do Evento Complementar: o complementar de um evento “A” corresponde a todos os elementos do Espaço Amostral que não pertencem a “A”, ou seja, para “B” sem complementar de “A”, B precisa acontecer quando “A” não acontecer.

Novamente, lembre-se do dado. O complementar de ???? = {1, 2, 3} será ~C = {4, 5, 6}. Relembre as fórmulas para os complementares da União e da Interseção.

Probabilidade Condicional

Agora vamos finalizar o resumo sobre Probabilidade para SEFAZ-RJ com a Probabilidade Condicional.

Probabilidade Condicional: trata-se dos casos de probabilidade de um evento ocorrer, sabendo que outro já ocorreu.

P = casos favoráveis / casos possíveis

Vamos exemplificar

Imagine que temos um saco com 10 bolas, 4 vermelhas e 6 azuis. Se retiramos uma bola vermelha (sem devolvê-la), qual a probabilidade de a próxima bola ser azul?

Simples. Ao retirar a primeira bola, ficam 9 bolas (3 vermelhas e 6 azuis), correto? Então, a probabilidade de a próxima bola ser azul é 3/9 ou 2/3.

Atente-se a duas características importantes.

Se dois eventos são independentes, a probabilidade condicionada é o próprio evento, pois um não influencia no outro.

Probabilidade condiciona de eventos independentes:

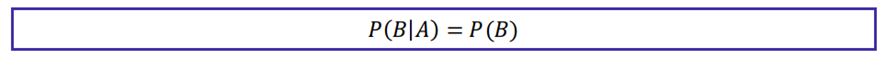
Além disso, a interseção de eventos independentes é a seguinte:

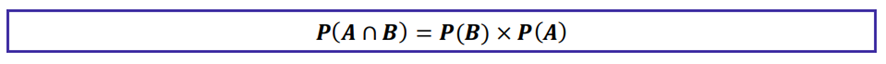
Não compreendeu? É bem simples.

Qual a probabilidade de sair 2 no lançamento do dado e em um segundo lançamento 3? É 1/6 E 1/6, logo 1/6 x 1/6 = 1/36.

Considerações Finais

Pessoal, chegamos ao final do resumo sobre Probabilidade para SEFAZ-RJ, tema da Estatística. Espero que o artigo tenha sido útil.

Trata-se de um tema eminentemente prático, assim não deixe de estudar o assunto na íntegra por nossas aulas, além de treinar por meio de questões de concurso em nosso sistema de questões.

Gostou do artigo? Siga-nos

https://www.instagram.com/resumospassarin

Cursos e Assinaturas

Prepare-se com o melhor material e com quem mais aprova em Concursos Públicos em todo o país!

Concursos Abertos

Concursos 2024