Permutações com Elementos Ordenados
Fala, pessoal!
Tudo bem com vocês?
Sextou!!!
E o que isso quer dizer no Estratégia? Que produzimos ainda mais!!! :)
Escrevi recentemente diversos artigos sobre temas espinhosos de Análise Combinatória. Esses temas foram motivados por questões interessantes que apareceram em provas de concursos.
Eis os links dos artigos: Permutações Caóticas, Partições Ordenadas, Lemas de Kaplansky e Combinações Completas.
O que me motivou a escrever este artigo de hoje foi uma questão que caiu no último domingo (29/09/2019) na prova para Assistente Administrativo da UFRPE.
Antes de começarmos o nosso bate-papo, deixo o convite para vocês seguirem o meu perfil no instagram @profguilhermeneves.
Dê uma olhada no enunciado e tente resolver.
(SUGEP 2019/UFRPE – Assistente Administrativo)
Cinco corredores competiram em uma corrida: Fred, George, Heloísa, Lúcia e Ronaldo. É conhecido que:
– Fred perdeu para George.
– Lúcia ganhou de Heloísa.
– Lúcia perdeu de George.
– George ganhou de Ronaldo.
Supondo que não houve empates, quantas possíveis ordens de finalização poderiam ter acontecido, dadas apenas essas informações?
a) 1
b) 6
c) 12
d) 18
e) 24
Questão que aparentemente é bem simples, mas que derruba o aluno com pouca base em Análise Combinatória, não é mesmo?
A questão mais antiga que me recordo nesse estilo foi na finada ESAF em 2004.
(ESAF 2004/MPU)
Paulo possui três quadros de Gotuzo e três de Portinari e quer expô-los em uma mesma parede, lado a lado. Todos os seis quadros são assinados e datados. Para Paulo, os quadros podem ser dispostos em qualquer ordem, desde que os de Gotuzo apareçam ordenados entre si em ordem cronológica, da esquerda para a direita. O número de diferentes maneiras que os seis quadros podem ser expostos é igual a
a) 20
b) 30
c) 24
d) 120
e) 360
Resolução
Vamos pensar na solução desse problema específico e depois vamos bolar uma solução geral.
Se desconsiderarmos a restrição exigida pelo problema, deveremos apenas permutar os 6 quadros. Isso pode ser feito de
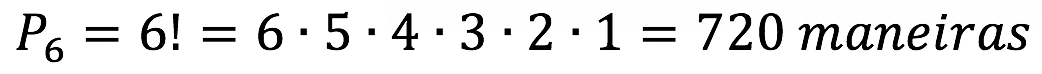
Vamos dar nomes aos quadros de Gotuzo: G1, G2, G3. Vamos considerar que essa ordem G1-G2-G3 é justamente a ordem cronológica.
Dessas 720 maneiras, os quadros de Gotuzo podem aparecer nas seguintes sequências (não necessariamente contiguamente, ou seja, um ao lado do outro).
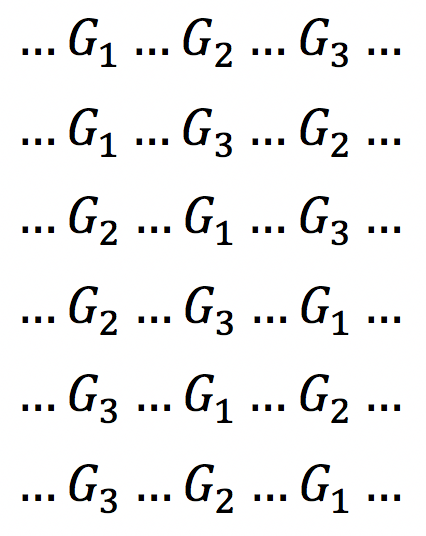
Acima eu descrevi todas as possíveis permutações dos 3 quadros de Gotuzo (3! = 6 maneiras de permutar os quadros de Gotuzo entre si).
As 720 maneiras estão regularmente distribuídas nas 6 possibilidades de organização cronológica descritas acima, ou seja, em cada uma das 6 possibilidades, há 720/6 = 120 maneiras de arrumar os quadros.
Como queremos os quadros de Gotuzo fiquem na ordem …G1…G2…G3…, então apenas a primeira possibilidade nos interessa.
Resposta: 120
Gabarito: D
Solução Geral
No problema anterior dos quadros de Gotuzo, nós dividimos a permutação de todos os 6 quadros (720 possibilidades) pelo número de permutações dos quadros que precisam ficar em determinada ordem (6 permutações).
Assim, a resposta do problema foi 720/6 = 120.
De uma maneira geral, se vamos permutar n elementos dos quais k deles devem estar em uma determinada ordem, o total de permutações será
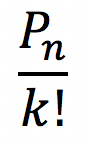
Vamos fazer outro exemplo antes de resolvermos a questão da UFRPE?
Exemplo: Quantos são os anagramas da palavra ARREPIOU em que as vogais figuram em ordem alfabética, mas não necessariamente juntas?
Resolução
O total de permutações sem a restrição de que as vogais são ordenadas é:
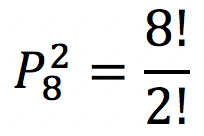
No cálculo acima, devemos dividir por 2! porque há duas letras R repetidas (permutação com repetição).
Entretanto, há 5 elementos que devem obedecer determinada ordem (as 5 vogais). Assim, o número de permutações pedido é
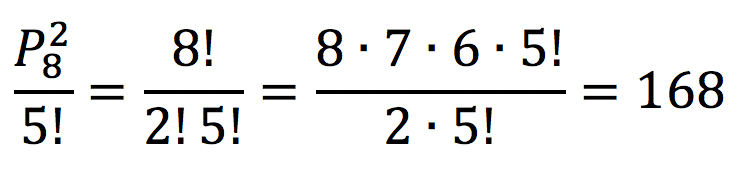
Veja como agora ficará fácil a questão da UFRPE.
(SUGEP 2019/UFRPE – Assistente Administrativo)
Cinco corredores competiram em uma corrida: Fred, George, Heloísa, Lúcia e Ronaldo. É conhecido que:
– Fred perdeu para George.
– Lúcia ganhou de Heloísa.
– Lúcia perdeu de George.
– George ganhou de Ronaldo.
Supondo que não houve empates, quantas possíveis ordens de finalização poderiam ter acontecido, dadas apenas essas informações?
a) 1
b) 6
c) 12
d) 18
e) 24
Resolução
George ganhou de Fred, Lúcia e Ronaldo. Como Lúcia ganhou de Heloísa, então George também ganhou de Heloísa (já que George ganhou de Lúcia). Logo, George ocupa o primeiro lugar.
Assim, devemos apenas nos preocupar nas posições 2, 3, 4 e 5.
Essas quatro posições serão ocupadas por Fred, Heloísa, Lúcia e Ronaldo. Portanto, devemos permutar essas 4 pessoas.
O único detalhe é que Lúcia ganhou de Heloísa, ou seja, elas devem ficar nessa ordem na fila (não necessariamente juntas). Não há outras informações no enunciado relacionando as outras pessoas.
Dessa forma, queremos permutar as 4 pessoas levando em consideração que há duas delas que devem obedecer determinada ordem.
Em casos como esse, devemos dividir o fatorial do total de pessoas pelo fatorial da quantidade de elementos que devem ficar em ordem.
O total de permutações possíveis é
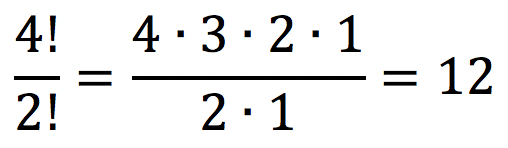
Gabarito: C
Espero que tenham gostado.
Um excelente fim de semana para todos. Forte abraço,
Guilherme Neves