Neste artigo, falarei um pouco sobre permutações caóticas – assunto recentemente cobrado em uma prova de Raciocínio Lógico da FCC.
Fala, pessoal!
Tudo bem?
Venho comentando que a FCC está cobrando uma enxurrada de assuntos implicitamente em seus editais.
Os assuntos mais cobrados em Raciocínio Matemático pela FCC são:
Clique aqui para conferir mais detalhes sobre Raciocínio Matemático na FCC.
Nos últimos dias, fiz uma profunda pesquisa em provas da FCC para tentar mapear tudo que a FCC pode cobrar dentro do tema “Raciocínio Matemático”.
Analisando as últimas provas de 2019, fiquei surpreso com a cobrança de um tema avançado de Análise Combinatória – as permutações caóticas.
Veja a questão:
(FCC 2019/Prefeitura do Recife – Assistente de Gestão Pública)
Os quatro funcionários de uma repartição trabalham cada um em uma mesa, todos na mesma sala. O chefe da repartição determinou que os funcionários trocassem de mesa entre si. Os funcionários podem ser realocados na sala de modo que nenhum funcionário passe a ocupar a mesa que ocupava antes da realocação
a) de 4 maneiras diferentes.
b) de 24 maneiras diferentes.
c) de 9 maneiras diferentes.
d) de 6 maneiras diferentes.
e) de 12 maneiras diferentes.
Aparentemente é uma questão bem tranquila. Puro engano!
O assunto envolvido nessa questão não é tratado na esmagadora maioria de livros do Ensino Médio.
A questão só é factível porque o número de funcionários é bem pequeno, ou seja, o candidato poderia descrever todas as possibilidades e marcar a resposta.
Sejam (a, b, c, d) os funcionários em suas posições originais. Queremos realocar os funcionários de modo que nenhum ocupe a sua posição original. Dizemos que essa é uma permutação caótica (ou desarranjo).
As permutações caóticas são:
(b, a, d, c); (c, a, d, b); (d, a, b, c); (c, d, a, b); (d, c, a, b); (b, d, a, c); (b, c, d, a); (c, d, b, a) e (d, c, b, a).
Logo, há 9 maneiras diferentes de realocar os funcionários de modo que nenhum funcionário ocupe a posição original.
Veja que com 4 pessoas já é bastante complicado descrever todas as permutações caóticas.
E se fossem 5 pessoas ou 8 pessoas?
Apresento-lhes agora a fórmula para calcular o número de permutações caóticas (desarranjos) de n objetos:
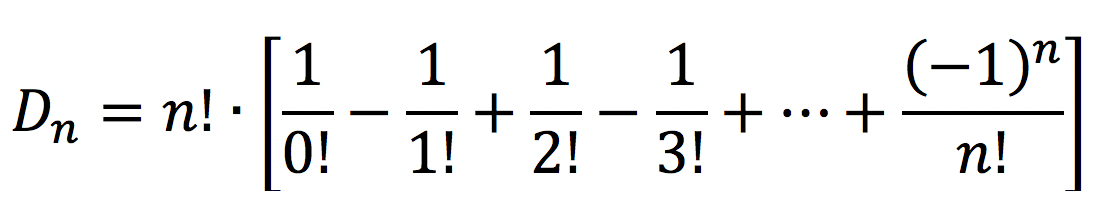
O termo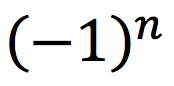 
simplesmente indica que os sinais das frações vão sendo alternados.
Por exemplo, para n = 4, temos:
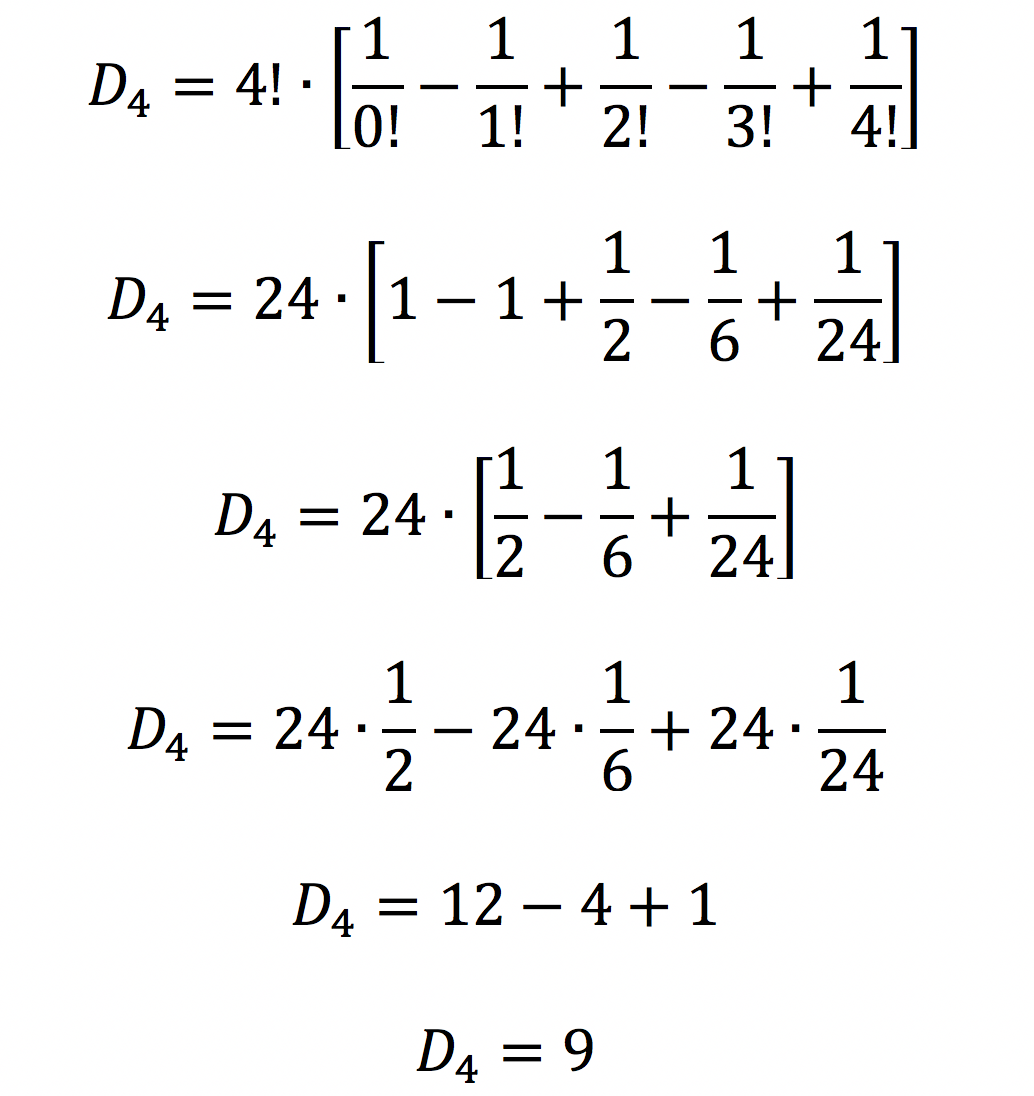
Veja o resultado para n = 6.
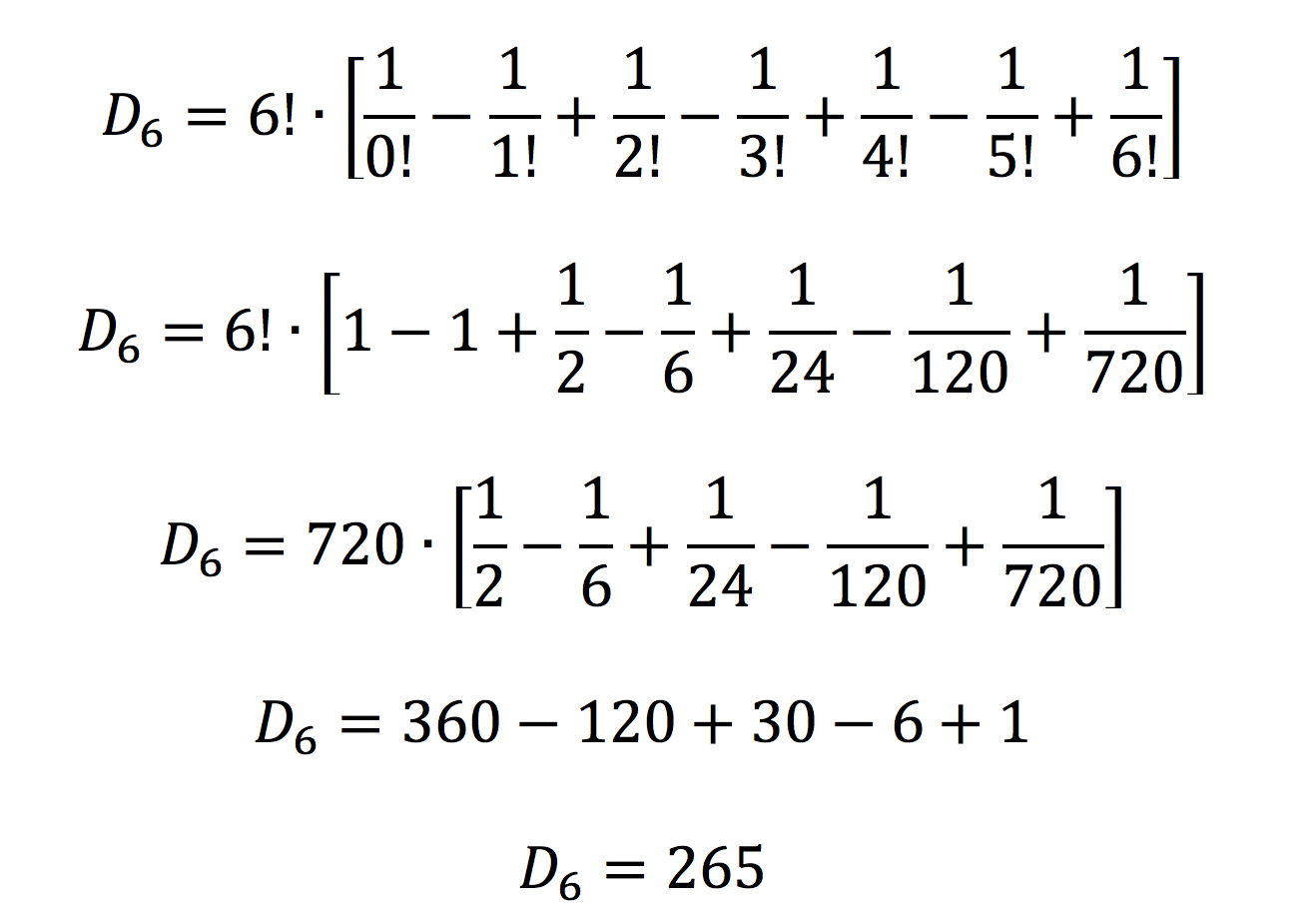
É claro que seria impossível você escrever todas as possibilidades à mão.
Mas, Guilherme, essa fórmula é muito complicada. Corro o risco de ficar nervoso e esquecê-la!
Calma, amigo. Agora vem a salvação. Existe uma maneira bem mais fácil e rápida de calcular o número de permutações caóticas.
É possível demonstrar que o número de permutações caóticas é o inteiro mais próximo de
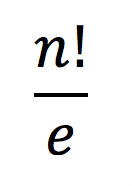
Na expressão acima, e é a constante de Euler: e = 2,718…
Observe para o caso n = 6.
De fato, para n = 6, o número de permutações caóticas é 265.
Vamos voltar à questão da FCC.
(FCC 2019/Prefeitura do Recife – Assistente de Gestão Pública)
Os quatro funcionários de uma repartição trabalham cada um em uma mesa, todos na mesma sala. O chefe da repartição determinou que os funcionários trocassem de mesa entre si. Os funcionários podem ser realocados na sala de modo que nenhum funcionário passe a ocupar a mesa que ocupava antes da realocação
a) de 4 maneiras diferentes.
b) de 24 maneiras diferentes.
c) de 9 maneiras diferentes.
d) de 6 maneiras diferentes.
e) de 12 maneiras diferentes.
Resolução
A questão pede o número de permutações caóticas de 4 elementos. O número de permutações caóticas é o inteiro mais próximo de
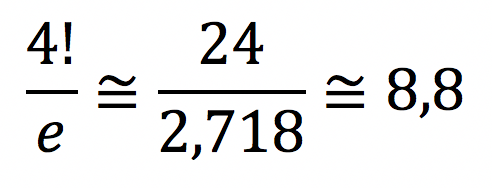
O inteiro mais próximo é 9. Logo, há 9 maneiras para realocar os funcionários de modo que nenhum ocupe a sua posição original.
Gabarito: C
Espero que tenham gostado! A partir de agora você vai torcer para cair permutação caótica outra vez. Assim, você vai deixar seus concorrentes para trás. :)
Forte abraço,
Guilherme Neves