Os Lemas de Kaplansky
Fala, pessoal!
Tudo bem?
Antes de começarmos o artigo de hoje, deixo o convite para vocês seguirem o meu perfil no instagram @profguilhermeneves.
Recentemente escrevi um artigo sobre uma questão da FCC que envolvia o conceito de Permutações Caóticas. Clique aqui para ler o artigo.
Permutação Caótica é um assunto avançado de Estatística e quase não aparece nos livros de Ensino Médio.
Fiquei então pensando: será que já apareceu alguma questão de outro assunto avançado de Análise Combinatória?
Tive vontade de escrever um pouco sobre os Lemas de Kaplansky, mas não fui em frente porque ainda não havia encontrado alguma questão de concurso sobre o tema.
Agora eu encontrei. :)
Eis a questão.
(FGV 2015/SSP-AM – Assistente Operacional)
Sete pessoas formam uma fila e duas delas serão escolhidas para receber um brinde. O número de maneiras diferentes de escolher duas pessoas da fila que não sejam vizinhas é:
a) 15;
b) 18;
c) 20;
d) 24;
e) 30.
Resolução
Vamos numerar as pessoas e formar um conjunto: {1, 2, 3, 4, 5, 6, 7}.
Para esse caso particular de escolhermos apenas duas pessoas, podemos utilizar um raciocínio mais simples: podemos escolher os dois elementos, sem restrição, de C(7,2) = 21 maneiras. Entretanto, não nos interessam os seguintes subconjuntos: {1,2}, {2,3}, {3,4}, {4,5}, {5,6}, {6,7}.
Logo, dos 21 subconjuntos, devemos excluir 6. O total de possibilidades é 21 – 6 = 15.
Mas esse raciocínio não resolveria um problema em que houvesse 10 pessoas e tivéssemos que escolher 4 pessoas não-vizinhas, por exemplo.
Vamos agora aprender a solução geral para esse tipo de problema.
Queremos formar um subconjunto de dois elementos no qual não há elementos consecutivos. Essa é exatamente a situação-problema resolvida pelos lemas de Kaplansky.
Falo no plural “lemas” porque o segundo lema de Kaplansky considera 1 e 7 como sendo consecutivos (basta pensar, por exemplo, que sábado e domingo são consecutivos).
Na nossa questão da FGV, 1 e 7 não são consecutivos e, portanto, será a situação-problema do Primeiro Lema de Kaplansky.
O raciocínio desenvolvido em 1943 por Kaplansky (Irving Kaplanky, matemático canadense) é o seguinte: marcaremos com um sinal “+” os elementos do conjunto que farão parte do subconjunto e marcaremos com o sinal “–“ os elementos que não farão parte do subconjunto.
Por exemplo, o subconjunto {1, 3} seria representado por + – + – – – –.
O subconjunto {4, 5}, que não é um subconjunto válido para o nosso problema, seria representado por – – – + + – –.
Para formar um subconjunto de 2 elementos não-consecutivos, devemos colocar 2 sinais “+” e 5 sinais “–“ em fila, sem que haja dois sinais + juntos.
Para tanto, vamos começar dispondo os 5 sinais “–“ com espaços vazios entre eles (os espaços vazios serão representados por chaves.
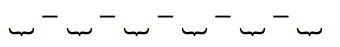
Observe que há 5 sinais “–“ e 6 espaços vazios onde podemos colocar os sinais de “+”.
Assim, há 6 espaços vazios e devemos escolher 2 para colocar os sinais de “+”. Como a ordem dos espaços vazios não importa, então isso pode ser feito de:
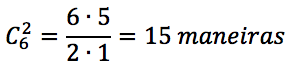
A resposta da questão é 15.
Gabarito: A
No caso geral, o conjunto original possui n elementos. Queremos formar subconjuntos de p elementos. Logo, teremos p sinais “+” e n – p sinais de “–“.
Ao dispor os n – p sinais “–“, teremos n – p + 1 espaços vazios para distribuir os sinais de “+”.
Logo, temos n – p + 1 espaços e devemos escolher p deles para distribuir os sinais de “+”, o que pode ser feito de
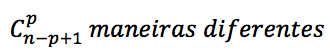
Esse raciocínio é exatamente o Primeiro Lema de Kaplansky, que pode assim ser enunciado:
O número de subconjuntos de p elementos de {1, 2, 3, …, n} nos quais não há elementos consecutivos é dado por:
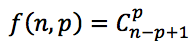
Se você entendeu o raciocínio desenvolvido, não precisará decorar a fórmula acima.
Vamos fazer mais um exemplo:
Guilherme Neves dará aulas em três dias diferentes na primeira semana de outubro de 2019. De quantos modos Guilherme pode escolher os dias das aulas se ele não quer dar aulas em dias consecutivos?
a) 10
b) 20
c) 35
d) 42
e) 210
Resolução
Perceba que, como estamos nos referindo à primeira semana de determinado mês, o primeiro e o último dia da semana não são consecutivos.
São 7 dias na primeira semana de outubro. Guilherme dará aula em 3 dias. Logo, teremos 3 sinais “+” e 4 sinais “–“.
Vamos colocar os 4 sinais “–“ e destacar os espaços vazios em que podemos distribuir os sinais de “+”.
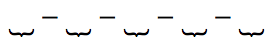
Temos 5 espaços vazios e devemos escolher 3 para colocar os sinais de “+”. Logo, o total de maneiras é:
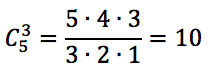
Gabarito: A
Pois bem, até agora nunca vi uma questão envolvendo o segundo lema de Kaplansky, mas vai que…
Segundo Lema de Kaplansky
Vamos agora considerar que 1 e n são consecutivos no conjunto {1, 2, …, n}. Isso é bem comum em questões envolvendo calendários. Por exemplo, o 31 de dezembro e 1 de janeiro são consecutivos, sábado e domingo são dias consecutivos, etc.
O Segundo Lema de Kaplansky diz que o número de subconjuntos com p elementos do conjunto {1, 2, 3, …, n}, em que 1 e n são considerados consecutivos, é igual a
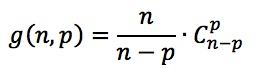
A fórmula acima é um pouco trabalhosa de ser demonstrada (a demonstração pode ser encontrada no livro Análise Combinatória e Probabilidade da Sociedade Brasileira de Matemática).
Não vale a pena memorizar essa fórmula, pois a relação custo-benefício é péssima: nunca vi cair em prova (até agora).
Por isso, vou ensinar o raciocínio da demonstração para que você não precise memorizar a fórmula.
Exemplo: O professor Paulo Bilynskyj decidiu praticar Crossfit 3 vezes por semana. De quantas maneiras Paulo pode escolher os dias de treino, se ele não quer praticar Crossfit em dias consecutivos?
a) 5
b) 6
c) 7
d) 8
e) 9
Resolução
Situação típica do Segundo Lema de Kaplansky, pois, como a atividade será feita periodicamente, sábado e domingo (último dia e primeiro dia da semana) são consecutivos.
Vamos considerar que Domingo = 1, Segunda-feira = 2, …, Sábado = 7. Assim, temos o conjunto {1, 2, 3, 4, 5, 6, 7}.
Na situação, 1 e 7 são consecutivos. Paulo precisa escolher 3 números não consecutivos. Pelo Segundo Lema de Kaplansky, isso pode ser feito de:
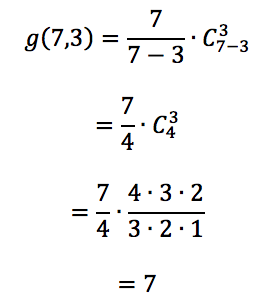
E como é o raciocínio sem decorar fórmula?
Pois bem, o segundo lema de Kaplansky é, na verdade, o primeiro lema aplicado duas vezes.
Vamos separar em dois casos: o elemento 1 foi escolhido e o elemento 1 não foi escolhido.
- Subconjuntos nos quais figura o elemento 1.
Se o elemento 1 foi escolhido, não podemos escolher os elementos 2 e 7, porque são elementos vizinhos ao número 1. Assim, devemos escolher 2 elementos não consecutivos no conjunto {3, 4, 5, 6}.
Vamos aplicar o primeiro lema de Kaplansky.
Para escolher 2 elementos dentre os 4, devemos ter dois sinais “–“ e dois sinais “+”. Os sinais “+” não podem ficar juntos porque os números escolhidos não são consecutivos. Começamos fixando os sinais de “–“.

Assim, temos 3 espaços vazios e devemos escolher 2 deles para colocar os sinais de “+”. Isso pode ser feito de
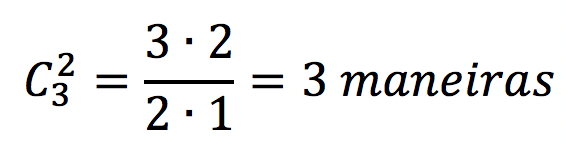
- Subconjuntos nos quais não figura o elemento 1.
Nesse caso, precisamos escolher 3 elementos não consecutivos no conjunto {2, 3, 4, 5, 6, 7}. Vamos aplicar novamente o primeiro lema de Kaplansky.
Para escolher 3 elementos dentre os 6, devemos ter três sinais “–“ e três sinais “+”. Os sinais “+” não podem ficar juntos porque os números não são consecutivos. Começamos fixando os sinais de “–“.
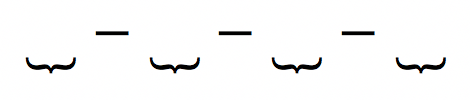
Assim, temos 4 espaços vazios e devemos escolher 3 deles para colocar os sinais de “+”. Isso pode ser feito de
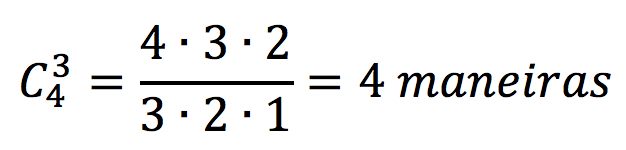
O total de maneiras é 3 + 4 = 7 maneiras.
Como vocês podem ver, o Segundo Lema de Kaplansky é, na verdade, o primeiro lema aplicado duas vezes: uma vez escolhendo o número 1 e outra vez excluindo o número 1.
Gabarito: C
Espero que tenham gostado.
Um forte abraço,
Guilherme Neves