Olá, pessoal. Tudo certo? No artigo de hoje veremos o Resumo sobre Médias para ISS-BH.
A média é um conceito imprescindível para qualquer prova de estatística, afinal é cobrado tanto direta quanto indiretamente, assim vamos tentar passar pelos principais pontos.
Sem mais delongas, vamos lá.
Vamos iniciar o Resumo sobre Médias para ISS-BH compreendendo sobre as medidas de posição.
Podemos definir as medidas de posição como as que representam uma posição em relação ao eixo horizontal da curva de frequência.
Vamos classificá-las da seguinte forma:
Medidas de tendência central:
Medidas separatrizes
A média aritmética é a mais conhecida por todos, assim não vamos precisar de grandes aprofundamentos.
Lembre-se que na omissão da questão sobre o tipo de média, utilizaremos a média aritmética para resolução.
Exemplo: Conjunto [1; 2; 3], logo média (x) é igual a 2
d1 = x1 – x = 1 – 2 = -1
d2 = x2 – x = 2 – 2 = 0
d3 = x3 – x = 3 – 2 = 1
Somatório = -1 + 0 + 1 = 0
Dando continuidade ao Resumo sobre Médias para ISS-BH, vejamos sobre a média ponderada.
A média ponderada é uma média que leva em consideração os pesos das medidas. Podemos descrever com a seguir formula:
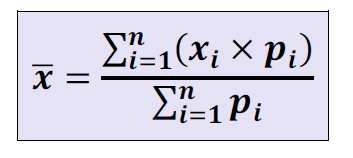
De fato a fórmula parece complicada, mas vamos exemplificar para ficar mais fácil.
(VUNESP/AVAREPREV/2020) Uma loja trabalha com produtos que são classificados em apenas três tipos.
Na tabela, constam os preços de venda de cada tipo do produto:
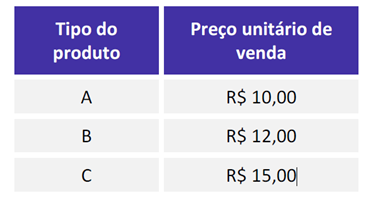
No último dia útil de funcionamento, foram vendidos produtos dos três tipos, sendo que, do total de unidades vendidas, ¼ foi de produtos do tipo A, 2/5 foi de produtos do tipo B, e o restante, de produtos do tipo C. Naquele dia, o preço médio unitário de venda dos produtos vendidos foi de
a) R$ 11,95.
b) R$ 12,30.
c) R$ 12,55.
d) R$ 13,50.
e) R$ 13,95.
ALTERNATIVA C.
Total de vendas:
A = ¼ = 25%
B = 2/5 = 40%
C = 100 – 25% – 40% = 35%
A = (10 x 0,25) + (12 x 0,4) + (15 x 0,35) / 1
A = 2,5 + 4,8 + 5,25 = 12,55
Tranquilo, não é mesmo? Vamos continuar.
Continuando o Resumo sobre Médias para ISS-BH, agora vamos conhecer as médias para dados agrupados. Vamos dividir em duas situações:
Média para Dados Agrupados por Valor
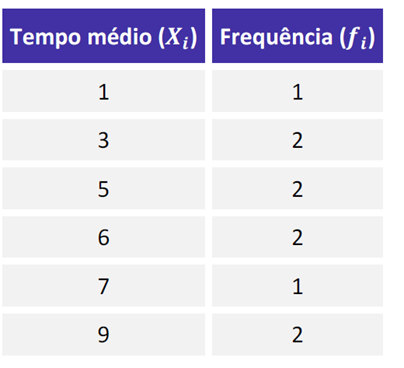
Agora basta multiplicar as variáveis Xi e fi e dividir pela somatória da frequência.
X = [(1 x 1) + (3 x 2) + (5 x 2) + (6 x 2) + (7 x 1) + (9 x 2)] / 10
X = (1 + 6 + 10 + 12 + 7 + 18) / 10
X = 54 / 10
X = 5,4
Média para Dados Agrupados por Classe (distribuição de frequência)
Pessoal, o cálculo é muito parecido, entretanto devemos encontrar os pontos médios primeiro.
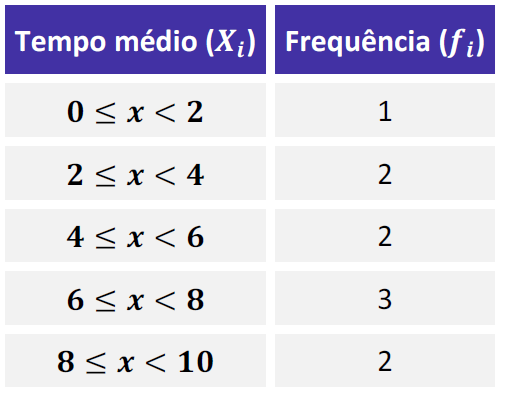
PM1 = (2 + 0) / 2 = 1
PM2 = (4 + 2) / 2 = 3
PM3 = (6 + 4) / 2 = 5
PM4 = (8 + 6) / 2 = 7
PM5 = (10 + 8) / 2 = 9
Agora o cálculo é exatamente igual ao que já sabemos:
X = [(1 x 1) + (3 x 2) + (5 x 2) + (7 x 3) + (9 x 2) / 10
X = (1 + 6 + 10 + 21 + 18) / 10
X = 56 / 10
X = 5,6
Podemos definir a Média Geométrica como a raiz n-ésima do produto de n elementos de um conjunto de dados.
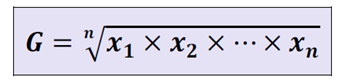
Uma opção importante, que pode ser observada pela fórmula, é que somente é calculada a média geométrica para números não-negativos.
Vamos verificar na prática como é calculada.
(FCC/ARTESP/2017) Considere as seguintes informações
II. (B) = média geométrica dos números 4, 6 e 12.
Substituindo os valores
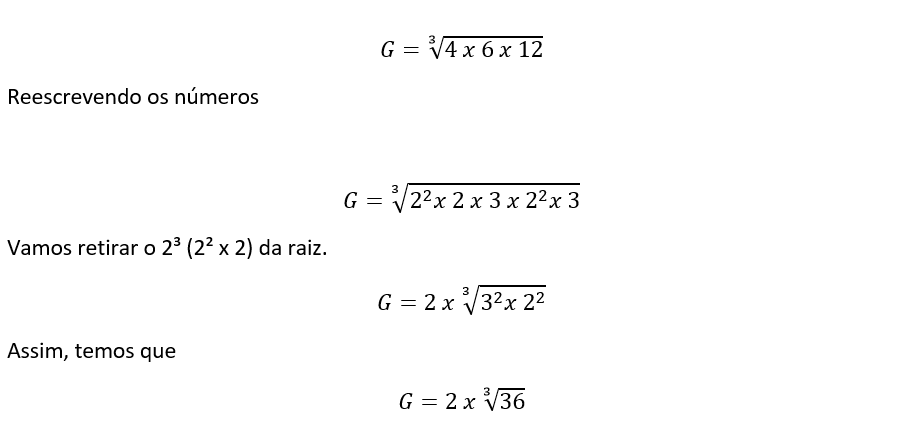
Aqui temos que “testar”, sabendo que o número de ser maior que 3 (3³ = 27) e menor de 4 (4³ = 64). O valor é de aproximadamente 3,3
G =2 x 3,3
Logo,
G = 6,6
Podemos definir a Média Harmônica como o inverso da média aritmética dos inversos.
Vamos aproveitar e ver o cálculo das média harmônica e geométrica com esse exemplo.
(FCC/ARTESP/2017) Considere as seguintes informações
I. (A) = média harmônica dos números 4, 6 e 12.
Para finalizar o Resumo sobre Médias para ISS-BH, vamos conhecer a relação entre as médias harmônicas, aritmética e geometria.
Utilizando novamente o exemplo, temos que a média aritmética será:
A = (4 + 6 + 12) / 3
A = 7,33
Então vamos comparar com o que havíamos encontrado
H=6
G=6,6
Propositalmente denominados a média aritmética de “A” para facilitar o seguinte bizu:
“As médias seguem a ordem alfabética”
A ≥ G ≥ H
Acredite, esse bizu pode garantir pontos preciosos na hora da prova sem praticamente realizar cálculos, então vale a pena memorizá-lo.
Pessoal, chegamos ao final do Resumo sobre Médias para ISS-BH. Espero que tenham gostado.
Obviamente trata-se de um resumo apenas com os pontos principais da matéria, assim não deixe de acompanhar as aulas para o aprofundamento necessário.
A matéria de estatística, como as matérias de exatas no geral, se a aprender com MUITO prática, assim não deixe de praticar por muitos exercícios em nosso sistema de questão.
Sistema de Questões (SQ) – Estratégia Concursos
Gostou do artigo? Não deixe de seguir
https://www.instagram.com/resumospassarin/
Prepare-se com o melhor material e com quem mais aprova em Concursos Públicos em todo o país.
Até mais e bons estudos!