Média Aritmética – você conhece as 3 formas de cálculo?

Média Aritmética – revisando as 3 formas de cálculo

Fala pessoal, tudo bem? Como vocês sabem, Média Aritmética é um assunto presente em uma grande variedade de concursos. O examinador pode te fornecer os dados de TRÊS formas diferentes, e cada uma delas terá um cálculo diferente:

1) dados em rol (lista de números);

2) dados em uma tabela de frequências;

3) dados em uma tabela com intervalos de classes.

Para te ajudar a relembrar, vou deixar neste artigo 3 questões resolvidas, uma sobre cada tipo. Vamos lá?

Média aritmética para dados em rol (lista de dados)

1. VUNESP – SPTRANS – 2012) O número de acidentes com motos, em determinada cidade, no decorrer de 5 dias, foi igual a:

6, 3, 4, 2, ?

Na média, o número de acidentes por dia foi 4,4. Se tivesse ocorrido mais um acidente no último dia (?), a média diária desses 5 dias teria sido de:

(A) 4,5.

(B) 4,6.

(C) 4,7.

(D) 4,8.

(E) 4,9.

RESOLUÇÃO:

        Se a média de acidentes ao longo dos 5 dias foi de 4,4, podemos escrever:

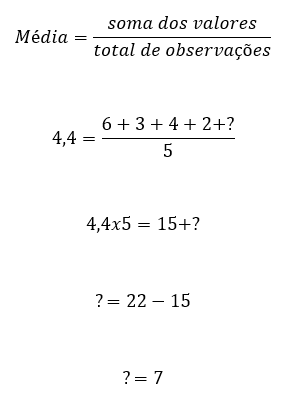
Portanto, no último dia ocorreram 7 acidentes. Se tivesse ocorrido mais 1, ou seja, um total de 8 acidentes, a média seria:

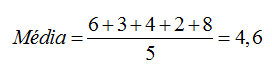
FORMA MAIS RÁPIDA: você poderia resolver essa questão rapidamente. Veja que houve o aumento de 1 acidente. Como, no cálculo da média, é preciso dividir por 5, então o aumento na média será de 1/5, ou seja, de 0,2. Assim, a nova média será:

4,4 + 0,2 = 4,6

Resposta: B

Média aritmética para tabela de frequências

2. VUNESP – TJM/SP – 2017) A tabela apresenta o número de acertos dos 600 candidatos que realizaram a prova da segunda fase de um concurso, que continha 5 questões de múltipla escolha.

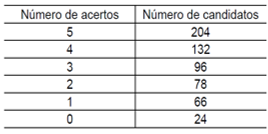
A média de acertos por prova foi de

(A) 3,57.

(B) 3,43.

(C) 3,32.

(D) 3,25.

(E) 3,19.

RESOLUÇÃO

Média aritmética para tabela com intervalos de classes

3. IDECAN – BOMBEIROS/DF – 2017) A média aritmética da distribuição de frequências a seguir é:

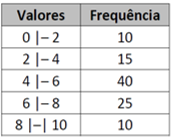
A) 4,9.

B) 5,2.

C) 5,3.

D) 5,5.

RESOLUÇÃO:

Aqui temos uma tabela com intervalos de classes. A fórmula de cálculo da média é:

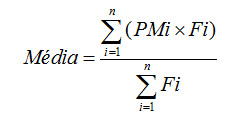
A aplicação desta fórmula é bem simples. Basta:

1) calcular os pontos médios de cada intervalo. Para isto basta somar os extremos de cada intervalo e dividir por 2. Por exemplo, o ponto médio do intervalo 0–2 é calculado assim:  (0 + 2) / 2 = 1. Fazendo isso para os demais intervalos, temos:

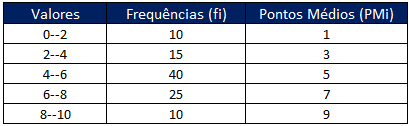
2) multiplicar cada ponto médio pela respectiva frequência, obtendo os termos PMi . fi: 

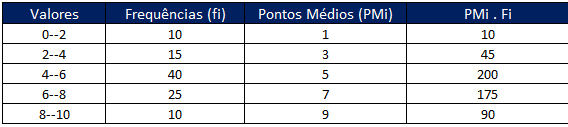
3) somar os termos da coluna PMi.fi, obtendo o numerador da fórmula da média (somatório de PMi.fi):

Em nosso exemplo, a soma da coluna PMi.fi é igual a 520.

4) somar os termos da coluna das frequências, obtendo o denominador da fórmula da média (somatório de fi):

Em nosso exemplo, a soma da coluna das frequências é 100.

5) dividir a soma da coluna PMi.fi pela soma da coluna das frequências, obtendo a média:

Portanto, média = 520 / 100 = 5,2.

Resposta: B

Espero que você tenha conseguido relembrar cada um dos cálculos!