Matemática ENEM – Revisão Geral – Aula Grátis com os assuntos mais cobrados no Exame

Você que precisa de um reforço para prova de Matemática do Exame Nacional do Ensino Médio, o Enem, eu tenho uma grande dica para você. Na noite desta quinta-feira, 9 de novembro, horário de Brasília, eu estarei AO VIVO com uma Aula Gratuita de Matemática para revisar os conteúdos mais cobrados na prova do Enem.

Estamos na reta final do Exame, pois o segundo dia de prova acontece neste domingo, 12 de novembro. Por isso, participe conosco e não perca essa oportunidade. Na aula, eu darei dicas de como você pode resolver as questões com tranquilidade e de forma assertiva.

Vou deixar o link para vocês assistirem. É a partir das 19h, não se esqueça!! Ahh! Você pode acompanhar a aula comigo. Vou disponibilizar meus slides para você fazer o download. Abraço e até a aula!

Baixe os Slides – Revisão de Matemática ENEM – Clique Aqui!

MATEMÁTICA ENEM – Os assuntos mais cobrados no Exame

Olá pessoal! Junto com o prof. Hugo Lima, leciono a disciplina de Matemática no Estratégia ENEM 2017. Ao contrário do nosso vestibular do ITA, cujo foco é em pontos mais aprofundados da Matemática, a prova do ENEM preza pelo conhecimento dos pontos mais básicos da matemática.

A ideia é trabalhar aqueles pontos mais presentes no dia a dia do cidadão comum. E é por isso que Porcentagens estão tão presentes nas provas dos últimos exames. Afinal, toda vez que você abrir um jornal, certamente vai se deparar com notícias que envolvem um destes dois conceitos (que, na realidade, estão intimamente ligados).

Veja esta notícia aqui:

Pergunta rápida para você: se a bolsa caiu 10% hoje, quanto ela precisa subir amanhã para retornar ao valor inicial de hoje? 10%? Mais de 10%? Menos de 10%?

Resposta: 

Suponha que você começou o dia de hoje com 100 reais na bolsa. Se houve uma queda de 10%, ao final do dia você terá:

100 x (1 – 10%) = 100 x (1 – 10/100) = 100 x  (1 – 0,10) = 100 x 0,90 = 90 reais

(veja que, para fazer uma REDUÇÃO percentual, basta multiplicar o valor original 100 por 1 menos o percentual de queda).

Amanhã você precisa que esses 90 reais sofram um aumento de p% para chegar de volta a 100 reais. Ou seja:

90 x (1 + p%) = 100

(1 + p%) = 100 / 90

1 + p% = 1,111

p% = 1,111 – 1

p = 0,111

p = 11,1 / 100

p = 11,1%

Ou seja, é preciso que amanhã haja um aumento SUPERIOR a 10% para retornarmos ao valor inicial.

Veja agora mais esta notícia:

Pergunta rápida: a fração presente na notícia (três em cada quatro) é maior ou menor do que o percentual fornecido (73%)?

Resposta:

Veja que precisamos comparar um número na forma fracionária (3 em cada 4, ou melhor, 3/4) com um número na forma percentual (73%). Para fazer a comparação, podemos levar estes dois números para a forma decimal. Veja:

3/4 = 1,5 / 2 = 0,75

73% = 73/100 = 0,73

Portanto, fica fácil observar que a fração 3/4 é MAIOR do que 73%.

Falando em porcentagens, veja esta questão cobrada no ENEM do último ano:

ENEM – 2016) O censo demográfico é um levantamento estatístico que permite a coleta de várias informações. A tabela apresenta os dados obtidos pelo censo demográfico brasileiro nos anos de 1940 e 2000, referentes à concentração da população total, na capital e no interior, nas cinco grandes regiões.

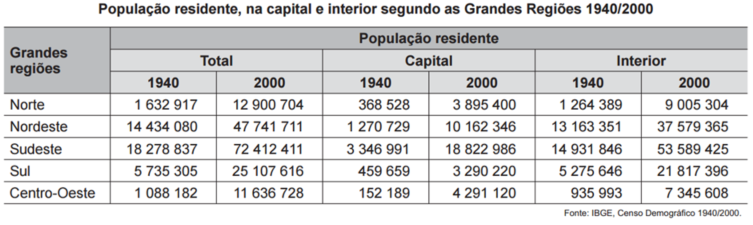 O valor mais próximo do percentual que descreve o aumento da população nas capitais da Região Nordeste é
A) 125%
B) 231%
C) 331%
D) 700%
E) 800%
RESOLUÇÃO: 
Vamos verificar no quadro somente o que é Região Nordeste e Capital (destaque em vermelho):

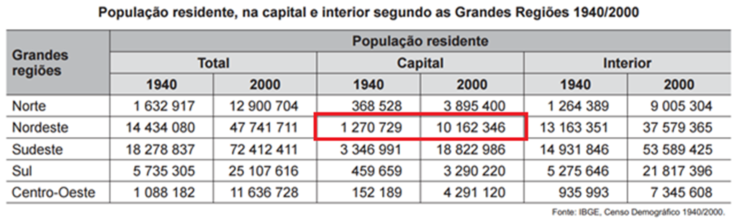
Veja que temos números muito grandes para trabalhar. Quando isto acontece, é importante que você seja capaz de realizar cálculos arredondados. Veja que as opções de resposta estão bem distantes umas das outras (125%, 231%, 331% etc), portanto não precisamos nos preocupar em realizar cálculos extremamente precisos. Vamos arredondar então, ok?

Em 1940, a população era de 1.270.729, ou seja, aproximadamente 1,27 milhões.
Em 2000, a população era de 10.162.346, ou seja, aproximadamente 10,16 milhões.
A diferença entre as populações é 10,16 – 1,27 = 8,89 milhões, aproximadamente.

Para calcular o percentual que esta diferença representa, em relação ao valor inicial (1,27), basta fazermos a divisão:

Percentual de aumento = Aumento / Valor inicial

Percentual de aumento = 8,89 / 1,27

Percentual de aumento = 7

Percentual de aumento = 700 / 100

Percentual de aumento = 700%

Resposta: D

Vamos resolver mais uma questão sobre Porcentagens?

ENEM – 2016) O setor de recursos humanos de uma empresa pretende fazer contratações para adequar-se ao artigo 93 da Lei n° 8.213/91, que dispõe:
Art. 93. A empresa com 100 (cem) ou mais empregados está obrigada a preencher de 2% (dois por cento) a 5% (cinco por cento) dos seus cargos com beneficiários reabilitados ou pessoas com deficiência, habilitadas, na seguinte proporção:
I. até 200 empregados ……………………………….. 2%;
II. de 201 a 500 empregados………………………… 3%;
III. de 501 a 1 000 empregados……………………… 4%;
IV. de 1 001 em diante………………………………….. 5%.
Disponível em: www.planalto.gov.br. Acesso em: 3 fev. 2015.
Constatou-se que a empresa possui 1 200 funcionários, dos quais 10 são reabilitados ou com deficiência, habilitados. Para adequar-se à referida lei, a empresa contratará apenas empregados que atendem ao perfil indicado no artigo 93. O número mínimo de empregados reabilitados ou com deficiência, habilitados, que deverá ser contratado pela empresa é
A) 74.
B) 70.
C) 64.
D) 60.
E) 53.
RESOLUÇÃO: 
Como a empresa tem mais de 1001 funcionários, ela precisa ter 5% de deficientes ou reabilitados. Hoje ela possui apenas 10 deficientes, então ela não cumpre a exigência, visto que 5% de 1200 são 60.
Portanto, será necessário que a empresa contrate x novos funcionários deficientes. Se ela fizer isso, o total de funcionários deficientes passa a ser 10 + x. Já o total de funcionários da empresa passaria a ser 1200 + x.
Para satisfazer a exigência, (10 + x) deve ser igual a 5% de (1200 + x). Ou seja:

10 + x = 5% (1200 + x)
10 + x = 60 + 0,05x
0,95x = 50
x = 52,6 funcionários

Como o número de funcionários deve ser inteiro, temos que a empresa deve contratar 53 novos funcionários deficientes ou reabilitados.
Resposta: E

Vamos trabalhar mais um pouco?

ENEM – 2016) Em uma empresa de móveis, um cliente encomenda um guarda-roupa nas dimensões 220 cm de altura, 120 cm de largura e 50 cm de profundidade. Alguns dias depois, o projetista, com o desenho elaborado na escala 1 : 8, entra em contato com o cliente para fazer sua apresentação. No momento da impressão, o profissional percebe que o desenho não caberia na folha de papel que costumava usar. Para resolver o problema, configurou a impressora para que a figura fosse reduzida em 20%.
A altura, a largura e a profundidade do desenho impresso para a apresentação serão, respectivamente,
A) 22,00 cm, 12,00 cm e 5,00 cm.
B) 27,50 cm, 15,00 cm e 6,25 cm.
C) 34,37 cm, 18,75 cm e 7,81 cm.
D) 35,20 cm, 19,20 cm e 8,00 cm.
E) 44,00 cm, 24,00 cm e 10,00 cm.

RESOLUÇÃO: 
A primeira coisa que o projetista fez foi fazer um desenho na escala 1:8. Isso significa que cada centímetro no desenho do projetista equivalem a 8 centímetros no mundo real. Portanto, dividindo as dimensões no mundo real por 8, obtemos as dimensões no desenho. Assim, ficamos com:

Altura = 220/8 = 27,5 cm
Largura = 120/8 = 15 cm
Profundidade = 50/8 = 6,25 cm

Depois, o projetista teve que reduzir em 20% a figura. Isso equivale a reduzir cada dimensão em 20%, que é o mesmo que multiplicar por 0,8, ou seja, calcular 80% das medidas atuais. Veja:

Altura = 27,5 x (1 – 20%) = 27,5 x 0,8 = 22 cm
Largura = 15 x (1 – 20%) = 15 x 0,8 = 12 cm
Profundidade = 6,25 x (1 – 20%) = 6,25 x 0,8 = 5 cm

Resposta: A

Quer estudar mais sobre proporções e porcentagens para o ENEM 2017? Assista esta minha aula gratuitamente:

COMO ESTUDAR MATEMÁTICA PARA ENEM 2017

Acompanho as provas do ENEM há muitos anos, primeiramente como aluno (fiz a prova do ENEM em 2000) e posteriormente como professor. Além disso, converso bastante com os alunos do Estratégia ENEM para entender as dificuldades que eles estão enfrentando e tentar ajudá-los a superar. Quero transmitir para você algumas estratégias e atitudes que eu costumo recomendar aos meus alunos para enfrentar a Matemática do ENEM.

Um primeiro ponto que você precisa ter em mente é o seguinte: as provas de Matemática do ENEM possuem muitas questões FÁCEIS! Isso mesmo! Embora a prova também possua questões difíceis, o fato é que um grande número de questões exige cálculos muito simples e básicos, focando mais na interpretação de problemas do dia-a-dia, e muitas vezes sem exigir que você tenha decorado qualquer fórmula. Além disso, há uma boa quantidade de questões de MÉDIA dificuldade, que já exigem um pouco mais de raciocínio ou aplicação de fórmulas simples. Analisando a prova de Matemática do ENEM 2016, que teve 45 questões, a distribuição das questões seria esta:

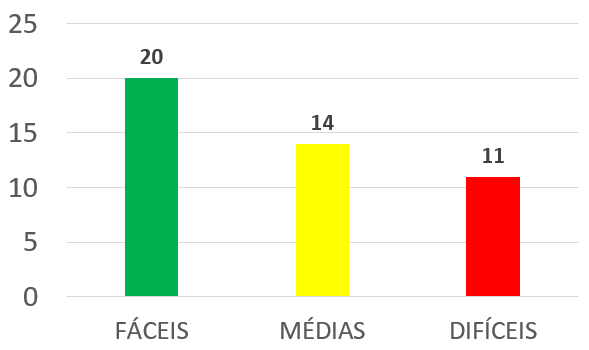
Se você acertasse todas as questões fáceis, 70% das médias e apenas 30% das difíceis, você teria 33 das 45 questões, o que já é um desempenho bem interessante. Vale lembrar que um bom resultado na prova de Matemática do ENEM é essencial para a sua classificação final, pois esta matéria é responsável por 45 das 180 questões objetivas do exame.

Exemplo de questão fácil de Matemática ENEM

Veja essa questão. Leia só o enunciado e tente resolver. Se não conseguir, leia a minha resolução. Mas repare que a questão não exigia praticamente nenhum conhecimento prévio, apenas a interpretação da situação-problema apresentada no enunciado e o uso de conhecimentos muito básicos da matemática (como a divisão e a porcentagem) para ser resolvida:

ENEM – 2016)   Cinco marcas de pão integral apresentam as seguintes concentrações de fibras (massa de fibra por massa de pão):

Marca A: 2g de fibras a cada 50g de pão;

Marca B: 5g de fibras a cada 40g de pão;

Marca C: 5g de fibras a cada 100g de pão;

Marca D: 6g de fibras a cada 90g de pão;

Marca E: 7g de fibras a cada 70g de pão;

Recomenda-se a ingestão do pão que possui a maior concentração de fibras.

Disponível em: www.blog.saude.gov.br. Acesso em: 25 fev. 2013.

A marca a ser escolhida é

A) A.

B) B.

C) C.

D) D.

E) E.

RESOLUÇÃO:

        Vamos calcular a concentração de fibras para cada marca de pão: Maior concentração de fibras:

Marca A: 2g de fibras a cada 50g de pão à 2/50 = 4%

Marca B: 5g de fibras a cada 40g de pão; à 5/40 = 12,5%

Marca C: 5g de fibras a cada 100g de pão à 5/100 = 5%

Marca D: 6g de fibras a cada 90g de pão à 6/90 = 6,6%

Marca E: 7g de fibras a cada 70g de pão à 7/70 = 10%

        A maior concentração de fibras está na marca B.

Resposta: B

Exemplo de questão média – Matemática ENEM

Veja ainda uma questão que eu classifico como “média dificuldade” na prova do ENEM 2016. Repare que ela até exige o uso de uma fórmula, porém trata-se de uma fórmula muito simples:

Média = soma dos valores divida pela quantidade de valores

Se você tiver estudado esta fórmula ao longo da sua preparação, e tiver resolvido alguns exercícios sobre cálculo de médias, certamente vai enfrentar essa questão sem grandes dificuldades.

ENEM – 2016) A permanência de um gerente em uma empresa está condicionada à sua produção no semestre. Essa produção é avaliada pela média do lucro mensal do semestre. Se a média for, no mínimo, de 30 mil reais, o gerente permanece no cargo, caso contrário, ele será despedido. O quadro mostra o lucro mensal, em milhares de reais, dessa empresa, de janeiro a maio do ano em curso.

Qual deve ser o lucro mínimo da empresa no mês de junho, em milhares de reais, para o gerente continuar no cargo no próximo semestre?

A) 26

B) 29

C) 30

D) 31

E) 35

RESOLUÇÃO:

        Seja X o lucro da empresa no mês de junho. A média deve ser, no mínimo, igual a 30 mil. Para resolver essa questão, basta lembrar que:

Média = Soma / quantidade

A soma dos lucros de todos os meses, incluindo o mês de junho, é:

Soma = 21 + 35 + 21 + 30 + 38 + X

Soma = 145 + X

A quantidade de valores envolvidos é 6 (temos seis meses). E a média é 30. Colocando na fórmula:

Média = Soma / quantidade

30 = (145+X) / 6

30 x 6 = 145 + X

180 = 145 + X

X = 180 – 145

X = 35 mil

Portanto, o lucro em junho deve ser de 35 mil reais.

Resposta: E

Exemplo de questão difícil – Matemática ENEM

Além das questões fáceis e médias, o ENEM distribui algumas questões difíceis ao longo da prova. É preciso se preparar para enfrentá-las, pois você não pode se dar ao luxo de “chutar” todas as questões difíceis. Só na última prova, 11 das 45 questões eram difíceis. Acertar essas questões pode te ajudar significativamente a obter um bom desempenho no ENEM.

Eu considero uma questão difícil em duas situações: quando ela exige o uso de fórmulas ou manipulações matemáticas mais complexas, ou quando ela exige grandes “sacadas”, isto é, a visualização de certos aspectos não muito usuais. Veja, por exemplo, a questão abaixo, que exigiu uma boa dose de visualização em 3 dimensões.

ENEM – 2016) É comum os artistas plásticos se apropriarem de entes matemáticos para produzirem, por exemplo, formas e imagens por meio de manipulações. Um artista plástico, em uma de suas obras, pretende retratar os diversos polígonos obtidos pelas intersecções de um plano com uma pirâmide regular de base quadrada. Segundo a classificação dos polígonos, quais deles são possíveis de serem obtidos pelo artista plástico

A) Quadrados, apenas.

B) Triângulos e quadrados, apenas.

C) Triângulos, quadrados e trapézios, apenas.

D) Triângulos, quadrados, trapézios e quadriláteros irregulares, apenas.

E) Triângulos, quadrados, trapézios, quadriláteros irregulares e pentágonos, apenas.

RESOLUÇÃO:

        Repare que para cada face da pirâmide de base quadrada interceptada pelo plano, teremos uma aresta do polígono que pode ser formado.

        A pirâmide de base quadrada tem 4 faces laterais e mais uma face na base. Logo, se o plano cruzar todas essas faces, será formada uma figura de 5 lados, ou seja, um pentágono, conforme mostrado abaixo:

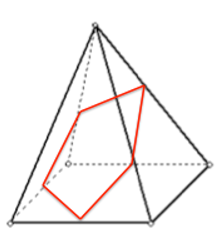
        Se o plano cruzar apenas 4 faces, será formado um quadrilátero irregular ou um trapézio. Se o plano coincidir com o plano da base, será formado um quadrado. Se o plano cruzar apenas 3 faces, será formado um triângulo. Portanto, o gabarito é a letra E.

Resposta: E

Como identificar questões fáceis, médias e difíceis na minha prova?

Saber identificar o grau de dificuldade das questões vai te ajudar a ter um ótimo resultado na prova do ENEM 2017. Para fazer isso, você precisa TREINAR BASTANTE, resolver MUITAS QUESTÕES anteriores do ENEM. Mas não basta “resolver por resolver”, apenas para fazer número. Ao enfrentar as questões, você precisa estar sempre atento para esta identificação do nível de dificuldade. Desta forma, em pouco tempo você estará captando algumas características que te permitem identificar rapidamente que uma questão é fácil. Com o tempo, só de “bater o olho” no enunciado você já vai ter uma boa noção da dificuldade. Você precisa ficar atento a detalhes como:

• questões que não exigem o uso de fórmulas;
• questões que apresentam, no próprio enunciado, as “regras” que devem ser usadas para se fazer uma análise matemática;

Como se preparar para a prova de Matemática do ENEM 2017?

Em primeiro lugar, gostaria de falar sobre o método que eu considero mais eficiente para você se preparar para o ENEM 2017. Estou falando do estudo online. 

Afinal, POR QUÊ EU ENTENDO QUE ESTUDAR POR AULAS ONLINE É UMA EXCELENTE OPÇÃO???

Para responder essa pergunta, deixo abaixo as principais vantagens que percebo no estudo online:

• excelente uso do seu tempo: você não perde tempo se arrumando (pode estudar de chinelo e camiseta rasgada rs), se deslocando no trânsito das grandes cidades, esperando nos intervalos entre as aulas, conversando com os colegas (sim, este é um ano que você vai precisar sacrificar um pouquinho a sua vida social!) etc.
• aproveitamento do “tempo morto”: como você pode baixar todas as aulas para o seu computador, tablet ou mesmo smartphone (áudios, vídeos e PDFs), é possível estudar em qualquer “tempo morto” que você tiver ao longo do dia – na fila da padaria, no ônibus, na espera de uma consulta médica etc.
• adequação ao seu ritmo: você estuda na velocidade que quiser, acelerando as aulas naqueles pontos que você tem mais facilidade, gastando mais tempo naqueles que tem mais dificuldade, parando quando estiver cansado, retomando o estudo quando bater aquele ânimo… Não é preciso esperar o professor tirar dúvida daquele colega que tem mais dificuldade que você – e, por outro lado, quando você tiver suas dúvidas, basta entrar em contato comigo através do fórum disponível na área do aluno. Eu e o professor Hugo Lima, também Engenheiro formado pelo Instituto Tecnológico de Aeronáutica (ITA) procuramos responder o mais rápido possível!

Enfim, eu sou suspeito para falar, pois realmente acredito muito nesta forma de estudo que a internet hoje nos permite realizar tão bem. Assim, sugiro que você gaste um tempinho resolvendo as questões da aula zero comigo, bem como assistindo os vídeos que disponibilizei nesta aula. O link é este abaixo:

CURSO MATEMATICA ENEM 2017 (VIDEOS, PDFs E FORUM DE DUVIDAS)

A propósito, vale dizer que nós do Estratégia Enem preparamos cursos completos de todas as disciplinas, para que você faça um estudo totalmente online e consiga atingir os seus objetivos em 2017! Clique no link abaixo para conferir as aulas iniciais dos demais cursos, também de forma totalmente gratuita!

Espero poder ajudá-lo a conseguir um excelente desempenho em Matemática no Enem 2017!