Matemática e Raciocínio Lógico TRT/SP (VÁRIOS CARGOS) – prova resolvida e gabarito
Caros alunos, vejam a seguir a prova resolvida de Matemática e Raciocínio Lógico-Matemático do TRT/SP e os meus comentários a respeito do gabarito divulgado pela banca FCC. Espero que tenham ido muito bem!
Mas antes de conferir a correção, não deixe de participar do Ranking TRT SP para conferir seu desempenho na prova. Clique na imagem abaixo para cadastrar seu gabarito:
Raciocínio Lógico – Técnico Judiciário – Área Administrativa (TJAA)
FCC – TRT/SP – 2018) Se o veículo ultrapassar os 50 km/h, então seu motorista será multado.
Uma afirmação equivalente à afirmação anterior é:
(A) Se o motorista não foi multado, então seu veículo ultrapassou os 50 km/h.
(B) O veículo não ultrapassou os 50 km/h e seu motorista não será multado.
(C) O veículo não ultrapassa os 50 km/h ou seu motorista é multado.
(D) Se o motorista foi multado, então seu veículo ultrapassou os 50 km/h.
(E) O motorista só será multado se o veículo ultrapassar os 50 km/h.
RESOLUÇÃO:
Temos a condicional p–>q onde:
p = o veículo ultrapassar os 50 km/h
q = seu motorista será multado
Ela equivale à condicional ~q–>~p e também à disjunção ~p ou q. Escrevendo ambas:
~q–>~p: “Se o motorista NÃO é multado, então o veículo NÃO ultrapassou os 50km/h”.
~p ou q: “O veículo NÃO ultrapassa os 50km/h OU seu motorista será multado”.
Temos esta última frase na alternativa C.
Resposta: C
FCC – TRT/SP – 2018) A tabela abaixo mostra os tempos de Fernanda em 5 dias seguidos de treinamento de corrida.
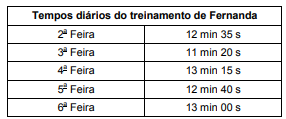
Nas duas semanas seguintes Fernanda também treinou 5 dias seguidos. Na primeira dessas duas semanas, Fernanda correu, cada um dos 5 dias, em um tempo igual ao menor tempo da tabela. Na segunda dessas duas semanas, Fernanda correu, cada um dos 5 dias, em um tempo igual ao maior tempo da tabela. Desse modo, o total de tempo de treinamento a mais, que Fernanda treinou na segunda dessas duas semanas em relação à primeira delas, foi igual a
(A) 9 minutos e 35 segundos.
(B) 8 minutos e 45 segundos.
(C) 10 minutos e 15 segundos.
(D) 9 minutos e 55 segundos.
(E) 8 minutos e 25 segundos.
RESOLUÇÃO:
Na primeira semana Fernanda correu, todos os dias, 11min 20s, ou seja, 11×60 + 20 = 680 segundos por dia.
Na segunda semana Fernanda correu, todos os dias, 13min 15s, ou seja, 13×60 + 15 = 795 segundos por dia.
A diferença, é de 5 x (795 – 680) = 5 x 115 = 575 segundos, que correspondem a 540 + 35, ou seja, 9×60 + 35, isto é, 9 minutos e 35 segundos.
Resposta: A
FCC – TRT/SP – 2018)Na sequência (5, 7, 9, 11, 6, 8, 10, 12, 7, 9, 11, 13, 8, 10, 12, 14, 9, 11, 13, 15, 10, 12, 14, 16, 11, . . .), o número 15 aparece pela primeira vez na 20a posição e aparecerá pela última vez na posição de número
(A) 44
(B) 41
(C) 43
(D) 42
(E) 40
RESOLUÇÃO:
Observe a sequência. Podemos dividir em 4 sequências alternadas:
5, 7, 9, 11, 6, 8, 10, 12, 7, 9, 11, 13, 8, 10, 12, 14, 9, 11, 13, 15, 10, 12, 14, 16, 11, . . .
Observe que a sequência em negrito é a que está mais “atrasada”, isto é, tem os números mais baixos. Portanto, o 15 vai aparecer pela última vez nesta sequência. Para isto, após o número 16 (azul), será preciso escrever mais 4 grupos de 4 números (começando com 11, 12, 13, 14), ou seja, mais 4×4 = 16 números, e mais o próximo número, que será o 15.
Assim, além dos 24 números que já temos até o 16, devemos escrever mais 16 números e, por fim, mais 1, totalizando 24 + 16 + 1 = 41. Esta é a última vez que aparece o 15.
Resposta: B
Raciocínio Lógico – Técnico Judiciário – Segurança
FCC – TRT/SP – 2018) O salário de Arthur equivale a 3/7 do salário de Bárbara. Para que o salário de ambos fosse igual, o salário de Arthur teria que aumentar em 130% e, depois disso, ainda ser acrescido de R$ 60,00. Nas condições descritas, a soma dos atuais salários de Arthur e Bárbara, em reais, é igual a
(A) 6.000,00
(B) 5.400,00
(C) 6.200,00
(D) 6.400,00
(E) 5.900,00
RESOLUÇÃO:
Sendo B o salário de Bárbara, podemos dizer que o de Arthur é de 3B/7. Devemos pegar o salário de Arthur, aumentar 130% (ou seja, multiplicar por 1 + 130% = 1 + 1,3 = 2,3) e então somar 60 reais para chegar no salário de Bárbara. Isto é:
2,3 x 3B/7 + 60 = B
6,9B/7 + 60 = B
60 = B – 6,9B/7
60 = 7B/7 – 6,9B/7
60 = 0,1B/7
420 = 0,1B
B = 4200 reais
O salário de Arthur é 3B/7 = 3.4200/7 = 3.600 = 1800 reais.
A soma dos salários é 4200 + 1800 = 6000 reais.
Resposta: A
FCC – TRT/SP – 2018) Do total de funcionários(as) de um tribunal, 20% têm menos de 40 anos de idade, e 70% são homens. Sabe-se ainda que 20% das mulheres que trabalham nesse tribunal têm menos de 40 anos de idade. A porcentagem do total de funcionários(as) desse tribunal que são homens e com 40 anos ou mais de idade é igual a
(A) 52%
(B) 48%
(C) 56%
(D) 54%
(E) 45%
RESOLUÇÃO:
Imagine que temos 100 funcionários. Como 20% (ou seja, 20) tem menos de 40 anos, podemos dizer que os outros 80 tem 40 anos ou mais.
Como 70% (ou seja, 70) são homens, podemos dizer que as mulheres são as 30 pessoas restantes.
Sabemos que 20% das 30 mulheres tem menos de 40 anos, ou seja, 0,20×30 = 6 mulheres tem menos de 40, de modo que as outras 30 – 6 = 24 mulheres tem 40 anos ou mais.
Os homens com 40 anos ou mais são a diferença entre 80 (pessoas com 40 anos ou mais) e 24 (mulheres com 40 anos ou mais), ou seja, 80 – 24 = 56.
Percentualmente, temos 56 / 100 = 56%.
Resposta: C
FCC – TRT/SP – 2018) Quinze fiscais iam vistoriar todos os estabelecimentos comerciais da zona sul da cidade em 25 dias, trabalhando 8 horas por dia cada um e todos com mesma produtividade. Depois de 5 dias completos desse serviço, a superintendência regional solicitou, em regime de urgência e com pagamento de hora extra, que os 15 funcionários passassem a trabalhar 10 horas por dia para finalizar a vistoria em menos dias do que os 25. Considerando que a solicitação foi atendida e que os funcionários continuaram o trabalho com mesma produtividade, a vistoria completa dos estabelecimentos comerciais da zona sul ocorreu em um total de
(A) 20 dias.
(B) 17 dias.
(C) 19 dias.
(D) 21 dias.
(E) 18 dias.
RESOLUÇÃO:
Sabemos que em 25 dias seriam realizadas todas as vistorias (100%). Assim, o percentual de vistorias feitas nos primeiros 5 dias é obtido por uma regra de três simples:
25 dias ————– 100% das vistorias
5 dias —————– P das vistorias
25.P = 5.100%
5.P = 100%
P = 20%
Portanto, já foram feitas 20% das vistorias, faltando realizar 80% delas. Agora vamos trabalhar com todas as grandezas. Sabemos que 100% das vistorias seriam feitas em 25 dias pelos 15 fiscais trabalhando 8 horas por dia. Queremos saber em quanto tempo faremos as 80% das vistorias restantes com os mesmos 15 fiscais trabalhando 10 horas por dia. Temos:
Fiscais Vistorias Horas por dia Dias
15 100% 8 25
15 80% 10 D
Quanto MAIS dias disponíveis, precisamos de MENOS fiscais para fazer MAIS vistorias, trabalhando MENOS horas por dia. Invertendo as grandezas inversamente proporcionais:
Fiscais Vistorias Horas por dia Dias
15 100% 10 25
15 80% 8 D
Montando a proporção:
25/D = (15/15) x (100% / 80%) x 10/8
25/D = 1 x (10/8) x (10/8)
1/D = 1 x (2/8) x (2/8)
1/D = 1 x (1/4) x (1/4)
1/D = 1/16
D = 16 dias
Portanto, precisamos dos 5 dias iniciais e mais 16 dias, totalizando 21 dias.
Resposta: D
Raciocínio Lógico – Analista Judiciário – Área Judiciária (AJAJ) e Oficial de Justiça Avaliador Federal (OJAF)
FCC – TRT/SP – 2018) Nair e Mariana receberam, no total, 198 processos para arquivar. Desse total, a maior parte foi entregue para Mariana. Depois da entrega, Mariana disse corretamente à Nair: “− Se eu lhe der um quarto dos processos que me deram para arquivar, você ficará com metade dos processos que vão sobrar para eu arquivar”. Nair respondeu para Mariana: “− Então eu proponho que você me dê um quarto dos processos que deram a você para arquivar”. Mariana aceita a proposta de Nair, o que implica dizer que Nair terá que arquivar x processos a mais do que teria que arquivar com a distribuição original de processos entre elas. Nas condições descritas, x é igual a
(A) 44
(B) 64
(C) 66
(D) 32
(E) 72
RESOLUÇÃO:
Imagine que Mariana recebeu M processos. Assim, Nair recebeu 198 – M.
Um quarto dos processos de Mariana são M/4 processos. Passando eles para Nair, teremos:
Nair: 198 – M + M/4 = 198 – 3M/4
Mariana = M – M/4 = 3M/4
Neste cenário, Nair tem metade dos processos de Mariana, ou seja,
Nair = Mariana/2
198 – 3M/4 = (3M/4)/2
198 – 3M/4 = 3M/8
198 = 3M/4 + 3M/8
198 = 6M/8 + 3M/8
198 = 9M/8
M = 198 x 8 / 9 = 176
Portanto, Mariana começa com 176 processos e Nair com os 198 – 176 = 22 restantes.
Relembrando a parte final do enunciado:
Nair respondeu para Mariana: “− Então eu proponho que você me dê um quarto dos processos que deram a você para arquivar”. Mariana aceita a proposta de Nair, o que implica dizer que Nair terá que arquivar x processos a mais do que teria que arquivar com a distribuição original de processos entre elas.
Veja que Mariana vai passar 176/4 = 44 processos para Nair. Este é o valor de x, ou seja, o número a mais de processo que Nair terá que arquivar.
Resposta: A
FCC – TRT/SP – 2018) Em um julgamento sobre danos ambientais, a acusação apresentou o dado de que os 5 fornos de uma olaria consumiam 50 toneladas de carbono trabalhando 10 horas diárias por 15 dias. A defesa propõe reduzir as atividades da olaria para 3 fornos trabalhando 9 horas diárias por 18 dias. Comparando o consumo de carbono da situação apresentada pela acusação (15 dias, 5 fornos, 10 horas diárias) com a situação proposta pela defesa (18 dias, 3 fornos, 9 horas diárias), houve uma redução do consumo de carbono, em toneladas, de
(A) 12,4
(B) 17,6
(C) 32,4
(D) 28,6
(E) 20,4
RESOLUÇÃO:
Temos a seguinte tabela:
Fornos Toneladas de carbono Horas diárias Dias
5 50 10 15
3 T 9 18
Para termos MAIS toneladas de carbono, precisamos de MAIS fornos trabalhando MAIS horas diárias por MAIS dias. Todas as grandezas são diretamente proporcionais. Podemos montar a proporção:
50/T = (5/3) x (10/9) x (15/18)
50/T = (5/3) x (10/9) x (5/6)
1/T = (5/3) x (1/9) x (1/6)
1x3x9x6 = 5x1x1xT
32,4 toneladas = T
A redução foi de 50 – 32,4 = 17,6 toneladas.
Resposta: B
FCC – TRT/SP – 2018) A sentença final de uma causa trabalhista indica que uma empresa terá que pagar R$ 2 450,00 para um trabalhador até o dia 10 de janeiro, com desconto de 15% caso pague antes dessa data. Caso pague depois do dia 10 de janeiro, a empresa terá que arcar com multa de 10% ao dia. Se a empresa fizer o pagamento ao trabalhador no dia 11 de janeiro, ela terá gasto x reais a mais do que se tivesse feito o pagamento no dia 9 de janeiro. Sendo assim, x, em reais, é igual a
(A) 306,25
(B) 428,75
(C) 857,50
(D) 122,50
(E) 612,50
RESOLUÇÃO:
Pagando no dia 9 de janeiro, temos um desconto de 15% sobre os 2450 reais, ou seja, vamos pagar:
Até 9 de janeiro = 2450 x (1 – 15%) = 2450 x 0,85 = 2082,50 reais
Pagando no dia 11 de janeiro, deverá ser acrescido 10% de multa em cima dos 2450 reais, ficando a conta em:
Dia 11 de janeiro = 2450 x (1 + 10%) = 2450 x 1,1 = 2695 reais
A diferença é de 2695 – 2082,50 = 612,50 reais.
Resposta: E
FCC – TRT/SP – 2018) Os meses de agosto e setembro têm, respectivamente, 31 e 30 dias. Às 16 horas do dia 4 de agosto de 2018, que é um sábado, um cronômetro, que estava inicialmente zerado, foi acionado. Esse cronômetro será desligado às 15 horas da primeira quarta-feira de outubro de 2018. O total de horas que o cronômetro indicará é igual a
(A) 1420
(B) 1369
(C) 1419
(D) 1439
(E) 1607
RESOLUÇÃO:
De 5 de agosto até 30 de setembro temos um total de (31 – 5+1 = 27) dias em agosto e 30 dias em setembro, totalizando 27 + 30 = 57 dias. Dividindo por 7, temos o resultado 8 e o resto 1. Isto significa que, a partir do dia 5 de agosto (domingo), temos 8 semanas completas, que vão de domingo ao próximo sábado, e mais 1 dia: domingo. Ou seja, 30 de setembro é domingo. A primeira quarta-feira de outubro será o dia 3.
Portanto, temos 57 + 2 = 59 dias completos (de 5 de agosto a 2 de outubro), que totalizam 59×24 = 1416 horas. Devemos somar ainda as 8 horas restantes do dia 4/agosto e as 15 horas restantes do dia 3 de outubro, totalizando 1416 + 8 + 15 = 1439 horas.
Resposta: D
FCC – TRT/SP – 2018) Almir, Beto, Célio e Danilo trabalham em uma repartição pública e suas idades são: 30, 31, 32 e 33 anos, não necessariamente nessa ordem. Suas ocupações são: auxiliar de escritório, contador, ouvidor e escriturário, ainda que não necessariamente nessa ordem. Sabe-se que:
− o auxiliar de escritório, que é o mais jovem dos quatro, é primo de Almir e sempre toma café com Beto;
− Célio, que é o mais velho dos quatro, mora no mesmo prédio do contador;
− Almir é dois anos mais novo que o escriturário.
Nas condições descritas acima, é correto afirmar que, necessariamente,
(A) Danilo é o contador.
(B) Célio é o escriturário.
(C) Almir é o ouvidor.
(D) Célio é o ouvidor.
(E) Beto é o escriturário.
RESOLUÇÃO:
Podemos montar a tabela:
| Pessoa | Idade | Ocupação |
| Almir | 30, 31, 32 e 33 | auxiliar, contador, ouvidor e escriturário |
| Beto | 30, 31, 32 e 33 | auxiliar, contador, ouvidor e escriturário |
| Célio | 30, 31, 32 e 33 | auxiliar, contador, ouvidor e escriturário |
| Danilo | 30, 31, 32 e 33 | auxiliar, contador, ouvidor e escriturário |
− o auxiliar de escritório, que é o mais jovem dos quatro, é primo de Almir e sempre toma café com Beto;
Isto mostra que nem Almir e nem Beto são auxiliares. E, além disso, eles não são os mais jovens. Temos:
| Pessoa | Idade | Ocupação |
| Almir | 31, 32 e 33 | contador, ouvidor e escriturário |
| Beto | 31, 32 e 33 | contador, ouvidor e escriturário |
| Célio | 30, 31, 32 e 33 | auxiliar, contador, ouvidor e escriturário |
| Danilo | 30, 31, 32 e 33 | auxiliar, contador, ouvidor e escriturário |
− Célio, que é o mais velho dos quatro, mora no mesmo prédio do contador;
Fica claro que Célio tem 33 anos, e não é contador:
| Pessoa | Idade | Ocupação |
| Almir | 31, 32 | contador, ouvidor e escriturário |
| Beto | 31, 32 | contador, ouvidor e escriturário |
| Célio | 33 | auxiliar, ouvidor e escriturário |
| Danilo | 30, 31, 32 | auxiliar, contador, ouvidor e escriturário |
− Almir é dois anos mais novo que o escriturário.
Fica claro que Almir não pode ter 33 nem 32 anos, nem pode ser o escriturário. Assim, sobra para ele apenas 31 anos, que ninguém mais pode ter:
| Pessoa | Idade | Ocupação |
| Almir | 31 | contador, ouvidor |
| Beto | 32 | contador, ouvidor e escriturário |
| Célio | 33 | auxiliar, ouvidor e escriturário |
| Danilo | 30 | auxiliar, contador, ouvidor e escriturário |
Vemos que o escriturário é o Célio, que é 2 anos mais velho que Almir. O auxiliar é Danilo, que é o mais jovem. Temos:
| Pessoa | Idade | Ocupação |
| Almir | 31 | contador, ouvidor |
| Beto | 32 | contador, ouvidor |
| Célio | 33 | escriturário |
| Danilo | 30 | auxiliar |
Podemos garantir que Célio é o escriturário (alternativa B).
Resposta: B
Raciocínio Lógico – Outros Analistas (Medicina, História etc)
FCC – TRT/SP – 2018) Para preparar um certo número de caixas, 15 funcionários de uma empresa trabalharam durante 8 horas, cada um preparando 7 caixas a cada 20 minutos. Já cansados, três dos funcionários foram embora e os que ficaram trabalharam por mais 6 horas, mais lentos, cada um deles preparando 7 caixas a cada 40 minutos. Ao todo, nessas 14 horas os funcionários conseguiram preparar um número de caixas
(A) entre 3350 e 3400
(B) entre 3150 e 3200
(C) entre 3200 e 3250
(D) entre 3250 e 3300
(E) entre 3300 e 3350
RESOLUÇÃO:
Na primeira etapa do trabalho, cada funcionário monta 7 caixas em 20 minutos. Em 8 horas, ou seja, 8×60 = 480 minutos, cada funcionário monta:
7 caixas ———— 20 minutos
C caixas ———–480 minutos
7 x 480 = C x 20
C = 7 x 24 = 168 caixas
Como são 15 funcionários temos 15 x 168 = 2520 caixas nesta primeira etapa.
Na segunda etapa, cada funcionário monta 7 caixas em 40 minutos. Trabalhando 6 horas (6 x 60 = 360 minutos), temos:
7 caixas ———- 40 minutos
N caixas ——— 360 minutos
7 x 360 = N x 40
7 x 9 = N
N = 63 caixas
Como são 15 – 3 = 12 funcionários, temos 12 x 63 = 756 caixas.
Ao todo, temos 2520 + 756 = 3276 caixas.
Resposta: D
FCC – TRT/SP – 2018) Uma sequência é formada pelos primeiros números ímpares positivos que possuem três, e apenas três divisores positivos distintos. A diferença entre o sexto e o quinto termos dessa sequência é
(A) 196
(B) 335
(C) 90
(D) 268
(E) 120
RESOLUÇÃO:
Os números com três divisores positivos distintos são aqueles cuja forma fatorada é n2, onde n é um fator primo. Como queremos apenas os ímpares, temos:
32, 52, 72, 112, 132, 172, …
A diferença entre o sexto e o quinto é:
172 – 132 =
289 – 169 =
120
Resposta: E
FCC – TRT/SP – 2018) Há dois anos, em uma empresa, a razão entre o número de funcionárias mulheres e o número de funcionários homens era 7/12. Hoje, sem que tenha aumentado ou diminuído o número total de funcionários (homens e mulheres) essa mesma razão é 9/10. A diferença do número de funcionárias mulheres de hoje e de dois anos atrás corresponde, em relação ao total de funcionários (homens e mulheres) da empresa, a um valor
(A) maior que 12%
(B) menor que 5%
(C) entre 5% e 8%
(D) entre 8% e 10%
(E) entre 10% e 12%
RESOLUÇÃO:
Sendo M e H o número inicial de homens e mulheres, podemos dizer que, inicialmente, tínhamos M/H = 7/12. Isto é,
12M = 7H
H = 12M/7
Como o número total de funcionários não mudou, podemos dizer que, se saíram “n” homens, entraram exatamente “n” mulheres, para deixar a nova razão igual a 9/10, ou seja:
9/10 = (M+n)/(H-n)
Isto é,
9H – 9n = 10M + 10n
9H = 10M + 19n
9.(12M/7) = 10M + 19n
108M/7 = 10M + 19n
108M = 70M +133n
38M =133n
n = 38M/133
A diferença entre o número de mulheres hoje e no início é de n = 38M/133.
O número total de funcionários é H + M = 12M/7 + M = 12M/7 + 7M/7 = 19M/7.
O percentual que a diferença corresponde em relação ao total de funcionários é dado por:
P = (38M/133) / (19M/7) = (38M/133) x (7 / 19M) = (2/133) x 7 = 14/133 = 0,105 = 10,5%
Resposta: E
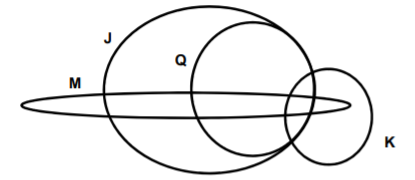
FCC – TRT/SP – 2018) Considere os conjuntos, suas respectivas intersecções e a existência de elementos em todas as regiões do diagrama.
A partir dessas informações é correto concluir que
(A) há elemento de M que seja elemento apenas de M e Q.
(B) qualquer elemento de J que não seja elemento de Q é elemento de M.
(C) há elemento de K que, além de ser de K, é também elemento de J, mas apenas de J.
(D) os elementos de M, que também são elementos de Q, não são apenas elementos desses dois conjuntos.
(E) todo e qualquer elemento de Q é elemento de pelo menos mais dois conjuntos.
RESOLUÇÃO:
(A) há elemento de M que seja elemento apenas de M e Q. –> ERRADO, não há região que pertença apenas a M e Q.
(B) qualquer elemento de J que não seja elemento de Q é elemento de M. –> ERRADO, existem elementos de J que não são de Q e nem são de M (estão em K).
(C) há elemento de K que, além de ser de K, é também elemento de J, mas apenas de J –> ERRADO, a interseção entre K e J também faz parte de Q.
(D) os elementos de M, que também são elementos de Q, não são apenas elementos desses dois conjuntos –> CERTO. Os elementos de M que também fazem parte de Q são também elementos de J.
(E) todo e qualquer elemento de Q é elemento de pelo menos mais dois conjuntos. –> ERRADO, pois existe uma região de Q que faz parte de apenas mais um conjunto: J.
Resposta: D
FCC – TRT/SP – 2018) Considere as seguintes afirmações:
I. Agnes é atriz ou Bernardo não é diretor.
II. Cíntia é estilista e Dinorá não é cantora.
III. Elivaldo não é segurança ou Fred é assistente.
IV. Se Bernardo é diretor, então Elivaldo não é segurança.
Sabe-se que as afirmações I e IV são falsas e que as afirmações II e III são verdadeiras. Sendo assim, é logicamente VERDADEIRA a alternativa
(A) Ou Bernardo não é diretor ou Fred não é assistente.
(B) Dinorá é cantora ou Agnes é atriz.
(C) Se Agnes é atriz, então Elivaldo é segurança.
(D) Fred não é assistente e Cíntia é estilista.
(E) Se Bernardo é diretor, então Dinorá é cantora.
RESOLUÇÃO:
Como I é falsa, sabemos que suas duas proposições são F, pois se trata de uma disjunção. Logo, podemos concluir que AGNES NÃO É ATRIZ e que BERNARDO É DIRETOR. Como IV é falsa, e se trata de uma condicional, temos V–>F, de modo que é verdade que BERNARDO É DIRETOR e também que ELIVALDO É SEGURANÇA. Para II ser verdadeira, precisamos que as duas informações da conjunção sejam V, ou seja, é verdade que CÍNTIA É ESTILISTA e que DINORÁ NÃO É CANTORA. Para III ser verdade, precisamos que FRED É ASSISTENTE seja V, pois sabemos que a parte de Elivaldo é falsa.
Com as conclusões em maiúsculas, podemos marcar a alternativa C, que apresenta uma condicional F–>V, que é verdadeira.
Resposta: C
Saudações.