Matemática e Raciocínio Lógico TJ SP – prova resolvida e gabarito extraoficial
Assista Aqui, Ao Vivo, a Correção da Prova TJ SP
Caros alunos,
Vejam abaixo o gabarito TJ SP (extraoficial) das provas de Matemática e Raciocínio Lógico, bem como a correção das questões. Espero que vocês tenham conseguido ir bem, assim como esse meu aluno aqui:

MATEMÁTICA TJ SP – PROVA RESOLVIDA E GABARITO EXTRAOFICIAL (ESCREVENTE)
VUNESP – TJ/SP – 2017) A empresa Alfa Sigma elaborou uma previsão de receitas trimestrais para 2018. A receita prevista para o primeiro trimestre é de 180 milhões de reais, valor que é 10% inferior ao da receita prevista para o trimestre seguinte. A receita prevista para o primeiro semestre é 5% inferior à prevista para o segundo semestre. Nessas condições, é correto afirmar que a receita média trimestral prevista para 2018 é, em milhões de reais, igual a
(A) 203.
(B) 198.
(C) 200.
(D) 195.
(E) 190
RESOLUÇÃO:
Sendo R2T a receita do segundo trimestre, sabemos que a do primeiro (180 milhões) foi 10% inferior a ela, ou seja,
180 = R2T x (1 – 10%)
180 = R2T x 0,90
R2T = 180 / 0,90 = 1800 / 9 = 200 milhões
A receita do primeiro semestre foi 180 + 200 = 380 milhões. Este valor é 5% menor que a receita do segundo semestre (RSS), ou seja,
380 = RSS x (1 – 5%)
380 = RSS x 0,95
RSS = 380 / 0,95 = 38000 / 95 = 400 milhões
A receita anual foi de 380 + 400 = 780 milhões. A média por trimestre, lembrando que temos 4 trimestres no ano, foi:
Média trimestral = 780 / 4 = 195 milhões
Resposta: D (195)
VUNESP – TJ/SP – 2017) A figura seguinte, cujas dimensões estão indicadas em metros, mostra as regiões R1 e R2, ambas com formato de triângulos retângulos, situadas em uma praça e destinadas a atividades de recreação infantil para faixas etárias distintas.
Se a área de R1 é 54 m², então o perímetro de R2 é, em metros, igual a
(A) 48.
(B) 36.
(C) 42.
(D) 54.
(E) 40.
RESOLUÇÃO:
A área do triângulo R1 é:
Área R1 = base . altura / 2
54 = x . 9 / 2
54 . 2 = 9x
108 = 9x
x = 108 / 9
x = 12
Assim, x+4 = 12+4 = 16. No triângulo retângulo R2, um cateto mede 12 e o outro 16. Este é um múltiplo do triângulo 3-4-5, basta multiplicar cada medida por 4. Logo a hipotenusa mede 20, e o seu perímetro é:
Perímetro R2 = 12 + 16 + 20 = 48
Você podia ter encontrado a hipotenusa também pelo teorema de pitágoras.
Resposta: A (48)
VUNESP – TJ/SP – 2017) Sabe-se que 16 caixas K, todas iguais, ou 40 caixas Q, todas também iguais, preenchem totalmente certo compartimento, inicialmente vazio. Também é possível preencher totalmente esse mesmo compartimento completamente vazio utilizando 4 caixas K mais certa quantidade de caixas Q. Nessas condições, é correto afirmar que o número de caixas Q utilizadas será igual a
(A) 18.
(B) 22.
(C) 10.
(D) 30.
(E) 28.
RESOLUÇÃO:
Veja que 16 K é igual a 40 Q, ou seja,
16K = 40Q
4K = 10Q
Se já colocamos 4K no compartimento, isto equivale a ter colocado 10Q. Assim, como no compartimento caberiam originalmente 40 Q, se já colocamos 10Q faltam colocar 40Q – 10Q = 30Q.
Resposta: D (30)
VUNESP – TJ/SP – 2017) Para segmentar informações, de modo a facilitar consultas, um painel de formato retangular foi dividido em 3 regiões quadradas, Q1, Q2 e Q3, e uma região retangular R, conforme mostra a figura, com dimensões indicadas em metros.
A área, em m², da região retangular R é corretamente representada por:
a) (1/3)x^2
b) (1/6).x^2
c) (1/8).x^2
d) (1/4).x^2
e) (1/12).x^2
RESOLUÇÃO:
O lado do quadrado Q1 mede 2x/3. Assim, os lados de Q2 e Q3, juntos, medem a diferença entre x e 2x/3, isto é,
x – 2x/3 = 3x/3 – 2x/3 = x/3
Como os quadrados Q2 e Q3 tem lados de mesma medida, cada lado deles deve medir (x/3)/2 = x/6.
Portanto, no retângulo R, o lado menor mede x/3 e o lado maior mede a diferença entre 2x/3 e x/6, que é:
2x/3 – x/6 = 4x/6 – x/6 = 3x/6 = x/2
A área do retângulo R é:
Área R = comprimento . largura
Área R = (x/2) . (x/3) = x^2 / 6
Resposta: B (1/6 . x^2)
VUNESP – TJ/SP – 2017) As figuras seguintes mostram os blocos de madeira A, B e C, sendo A e B de formato cúbico e C com formato de paralelepípedo reto retângulo, cujos respectivos volumes, em cm³, são representados por VA, VB e VC.
Se VA + VB = (1/2).VC, então a medida da altura do bloco C, indicada por h na figura, é, em centímetros, igual a
(A) 11.
(B) 12,5.
(C) 16.
(D) 15,5.
(E) 14.
RESOLUÇÃO:
Os volumes dos cubos A e B são:
VA = 5^3 = 125
VB = 10^= 1000
Utilizando a relação fornecida no enunciado:
VA + VB = VC/2
125 + 1000 = VC/2
1125 = VC/2
VC = 2250
O volume de C é dado pela multiplicação das dimensões, ou seja,
VC = 18.10.h
2250 = 18.10.h
225 = 18h
h = 225 / 18
h = 12,5
Resposta: B (12,5)
VUNESP – TJ/SP – 2017) Os preços de venda de um mesmo produto nas lojas X, Y e Z são números inteiros representados, respectivamente, por x, y e z. Sabendo-se que x + y = 200, x + z = 150 e y + z = 190, então a razão x/y é:
a) 1/3
b) 3/5
c) 3/8
d) 4/9
e) 2/3
RESOLUÇÃO:
Temos o sistema:
x + y = 200 –> y = 200 – x
x + z = 150 –> z = 150 – x
y + z = 190
Substituindo y e z nesta última equação pelas expressões obtidas anteriormente,
(200 – x) + (150 – x) = 190
350 – 2x = 190
350 – 190 = 2x
160 = 2x
x = 80
y = 200 – x = 200 – 80 = 120
Logo, x/y = 80/120 = 8/12 = 2/3
Resposta: E (2/3)
Não perca a nossa correção em vídeo AO VIVO. Será hoje às 18 horas! Inscreva-se gratuitamente aqui:
RACIOCÍNIO LÓGICO TJ SP – PROVA RESOLVIDA E GABARITO EXTRAOFICIAL (ESCREVENTE)
VUNESP – TJ/SP – 2017) Uma negação lógica para a afirmação “João é rico, ou Maria é pobre” é:
(A) João é rico, e Maria não é pobre.
(B) João não é rico, ou Maria não é pobre.
(C) Se João não é rico, então Maria não é pobre.
(D) Se João é rico, então Maria é pobre.
(E) João não é rico, e Maria não é pobre.
RESOLUÇÃO:
Temos a proposição “p ou q” no enunciado, onde:
p = João é rico
q = Maria é pobre
A sua negação é “~p e ~q”, em que:
~p = João não é rico
~q = Maria não é pobre
Ou seja,
“João não é rico E Maria não é pobre”
Resposta: E (João não é rico, e Maria não é pobre)
VUNESP – TJ/SP – 2017) “Existe um lugar em que não há poluição” é uma negação lógica da afirmação:
(A) Em alguns lugares, pode não haver poluição.
(B) Em alguns lugares, não há poluição.
(C) Em alguns lugares, há poluição.
(D) Em todo lugar, há poluição.
(E) Em todo lugar, não há poluição.
RESOLUÇÃO:
Para contradizer o autor da frase, precisamos mostrar que NÃO existe um lugar em que não há poluição. Ou seja, mostrar que em TODO lugar há poluição. Temos isso na alternativa D.
Resposta: D (Em todo lugar, há poluição)
VUNESP – TJ/SP – 2017) Considerando falsa a afirmação “Se Ana é gerente, então Carlos é diretor”, a afirmação necessariamente verdadeira
é:
(A) Ana não é gerente, ou Carlos é diretor.
(B) Ana não é gerente, e Carlos não é diretor.
(C) Ana é gerente.
(D) Ana é gerente, e Carlos é diretor.
(E) Carlos é diretor.
RESOLUÇÃO:
Temos a condicional p–>q em que:
p = Ana é gerente
q = Carlos é diretor
Se esta frase é falsa, sua negação é verdadeira. A sua negação é dada por “p e não-q”, ou seja:
“Ana é gerente E Carlos NÃO é diretor”
Logo, podemos afirmar que Ana é gerente, o que nos permite marcar a alternativa C.
Resposta: C (Ana é gerente)
VUNESP – TJ/SP – 2017) Uma afirmação equivalente para “Se estou feliz, então passei no concurso” é:
(A) Passei no concurso e não estou feliz.
(B) Estou feliz e passei no concurso.
(C) Se não passei no concurso, então não estou feliz.
(D) Se passei no concurso, então estou feliz.
(E) Não passei no concurso e não estou feliz.
RESOLUÇÃO:
Temos a condicional p–>q em que:
p = estou feliz
q = passei no concurso
As suas equivalências “manjadas” são:
~q–>~p: “Se NÃO passei no concurso, então NÃO estou feliz”
~p ou q: “NÃO estou feliz OU passei no concurso”
Temos na alternativa C uma dessas equivalências.
Resposta: C (Se não passei no concurso, então não estou feliz)
VUNESP – TJ/SP – 2017) Sabendo que é verdadeira a afirmação “Todos os alunos de Fulano foram aprovados no concurso”, então é necessariamente verdade:
(A) Se Carlos não foi aprovado no concurso, então ele não é aluno de Fulano.
(B) Fulano não foi aprovado no concurso.
(C) Se Elvis foi aprovado no concurso, então ele é aluno de Fulano.
(D) Fulano foi aprovado no concurso.
(E) Se Roberto não é aluno de Fulano, então ele não foi aprovado no concurso.
RESOLUÇÃO:
Vamos julgar cada opção de resposta:
(A) Se Carlos não foi aprovado no concurso, então ele não é aluno de Fulano.
Como Carlos não foi aprovado, ele NÃO pode mesmo ser aluno de Fulano (pois todos os alunos de Fulano foram aprovados). Este é o gabarito.
(B) Fulano não foi aprovado no concurso.
ERRADO, nada podemos afirmar sobre Fulano, e sim sobre os alunos dele.
(C) Se Elvis foi aprovado no concurso, então ele é aluno de Fulano.
ERRADO, o fato de todos os alunos de Fulano serem aprovados NÃO significa que todos os aprovados foram alunos dele.
(D) Fulano foi aprovado no concurso.
ERRADO, nada podemos afirmar sobre Fulano.
(E) Se Roberto não é aluno de Fulano, então ele não foi aprovado no concurso
ERRADO, é possível que outras pessoas, que NÃO tenham sido alunas de Fulano, também tenham sido aprovadas.
Resposta: A (Se Carlos não foi aprovado no concurso, então ele não é aluno de Fulano)
VUNESP – TJ/SP – 2017) Se Débora é mãe de Hugo, então Marcelo é baixo. Se Carlos não é filho de Débora, então Neusa não é avó dele. Sabendo-se que Marcelo é alto ou que Neusa é avó de Carlos, conclui-se corretamente que
(A) Débora não é mãe de Hugo, ou Carlos é filho de Débora.
(B) Hugo e Carlos são irmãos.
(C) Neusa é mãe de Débora.
(D) Hugo e Carlos não são irmãos.
(E) Débora não é mãe de Hugo, e Carlos é filho de Débora.
RESOLUÇÃO:
ATENÇÃO, POIS ESTA QUESTÃO PERMITE DUAS INTERPRETAÇÕES POSSÍVEIS. VOU COMEÇAR PELA QUE ACREDITO SER A VISÃO DO EXAMINADOR.
Temos essas duas premissas:
P1: Se Débora é mãe de Hugo, então Marcelo é baixo.
P2: Se Carlos não é filho de Débora, então Neusa não é avó dele.
Se soubermos que Marcelo é alto, então “Marcelo é baixo” é F. Deste modo, podemos concluir que “Débora é mãe de Hugo” deve ser F, ou seja, Débora não é mãe de Hugo.
Se soubermos que “Neusa é avó de Carlos”, o trecho “Neusa não é avó dele” em P2 deve ser F. Assim, “Carlos não é filho de Débora” é F, de modo que Carlos é filho de Débora.
Juntando tudo: sabendo-se que Marcelo é alto ou que Neusa é avó de Carlos, podemos concluir que “Débora não é mãe de Hugo, ou Carlos é filho de Débora”.
Esta resolução leva a um único gabarito, presente na alternativa A.
A outra resolução possível é aquela em que consideramos a última informação como sendo uma proposição composta. Veja a seguir.
Temos 3 premissas, todas elas proposições compostas. Devemos utilizar o método do chute.
P1: Se Débora é mãe de Hugo, então Marcelo é baixo.
P2: Se Carlos não é filho de Débora, então Neusa não é avó dele.
P3: Marcelo é alto ou Neusa é avó de Carlos.
“Chutando” que Débora é mãe de Hugo, em P1 é preciso que Marcelo é baixo também seja V para que a condicional seja respeitada.
Com isso, em P3 vemos que “Marcelo é alto” é F, de modo que Neusa é avó de Carlos precisa ser V para a disjunção ser respeitada.
Em P2, como “Neusa não é avó dele” é F, precisamos que “Carlos não é filho de Débora” seja F também, de modo que Carlos é filho de Débora.
Veja que foi possível deixar todas as premissas verdadeiras. As conclusões que podemos tirar estão todas sublinhadas.
Com elas em mãos, vamos analisar as alternativas de resposta:
(A) Débora não é mãe de Hugo (F), ou Carlos é filho de Débora (V) –> disjunção VERDADEIRA.
(B) Hugo e Carlos são irmãos –> VERDADE, ambos são filhos de Débora.
(C) Neusa é mãe de Débora –> não podemos afirmar isso. Sabemos que Neusa é avó de Carlos (filho de Débora), mas ela pode ser a avó paterna.
(D) Hugo e Carlos não são irmãos –> FALSO, eles são irmãos.
(E) Débora não é mãe de Hugo (F), e Carlos é filho de Débora (V) –> conjunção FALSA.
Note que chegamos a 2 respostas possíveis. Vamos agora trocar o nosso chute, passando para a hipótese de que Débora NÃO é mãe de Hugo. Com isso, P1 é uma condicional verdadeira, independentemente do valor lógico de “Marcelo é baixo”, pois a primeira parte da condicional é F. Veja que, nesta situação, é possível deixar as outras 2 premissas verdadeiras também. Por exemplo, basta assumir que Carlos É filho de Débora e que Marcelo é alto. Mas atenção, essa não é a única combinação possível. É possível que as informações verdadeiras sejam outras… mas este caso já é suficiente para vermos que não dá para afirmar que Hugo e Carlos são irmãos, pois é possível deixar as 3 premissas verdadeiras sendo apenas um deles filho de Débora. Assim, sobra apenas a alternativa A.
Acredito que a VUNESP deve ter considerado a primeira forma de resolução, bem mais simples que esta última.
Resposta: A (Débora não é mãe de Hugo, ou Carlos é filho de Débora)
VUNESP – TJ/SP – 2017) Em um edifício com apartamentos somente nos andares de 1º ao 4º, moram 4 meninas, em andares distintos: Joana, Yara, Kelly e Bete, não necessariamente nessa ordem. Cada uma delas tem um animal de estimação diferente: gato, cachorro, passarinho e tartaruga, não necessariamente nessa ordem. Bete vive reclamando do barulho feito pelo cachorro, no andar imediatamente acima do seu. Joana, que não mora no 4º, mora um andar acima do de Kelly, que tem o passarinho e não mora no 2ºandar. Quem mora no 3ºandar tem uma tartaruga. Sendo assim, é correto afirmar que
(A) o gato é o animal de estimação da menina que mora no 1ºandar.
(B) Kelly não mora no 1ºandar.
(C) Bete tem um gato.
(D) Yara mora no 4º andar e tem um cachorro.
(E) Joana mora no 3º andar e tem um gato.
RESOLUÇÃO:
Temos 4 amigas, 4 animais e 4 andares. Podemos montar a tabela:
| Amiga | Animal | Andar |
| Joana | Gato, cachorro, passarinho ou tartaruga | 1, 2, 3 ou 4 |
| Yara | Gato, cachorro, passarinho ou tartaruga | 1, 2, 3 ou 4 |
| Kelly | Gato, cachorro, passarinho ou tartaruga | 1, 2, 3 ou 4 |
| Bete | Gato, cachorro, passarinho ou tartaruga | 1, 2, 3 ou 4 |
Analisando as demais informações:
Bete vive reclamando do barulho feito pelo cachorro, no andar imediatamente acima do seu.
Desta frase podemos notar que Bete NÃO tem o cachorro e NÃO mora no 4º andar.
Joana, que não mora no 4o , mora um andar acima do de Kelly, que tem o passarinho e não mora no 2o andar.
Nesta frase vemos que Joana também NÃO mora no 4º andar, e nem a Kelly. Ainda vemos que a Kelly tem o passarinho e não mora no 2º andar. Veja que o 4º andar sobra para a Yara.
Colocando todas as informações até aqui na tabela, temos:
| Amiga | Animal | Andar |
| Joana | Gato, cachorro, |
1, 2, 3 |
| Yara | Gato, cachorro, |
|
| Kelly | 1, |
|
| Bete | Gato, |
1, 2, 3 |
Veja que Joana mora 1 andar acima do de Kelly. Kelly pode morar somente no 1º ou 3º andares. Se Kelly morasse no 3º, Joana deveria morar no 4º, mas este já é de Yara. Assim, Kelly deve morar no 1º, de modo que Joana mora no 2º. Sobra o terceiro andar para Bete:
| Amiga | Animal | Andar |
| Joana | Gato, cachorro, |
|
| Yara | Gato, cachorro, |
|
| Kelly | 1, |
|
| Bete | Gato, |
Quem mora no 3º andar tem uma tartaruga.
Ou seja, Bete tem a tartaruga.
Como o cachorro vive 1 andar acima de Bete, ele deve viver no quarto andar, sendo de Yara. Sobra o gato para Joana:
| Amiga | Animal | Andar |
| Joana | Gato, |
|
| Yara | ||
| Kelly | 1, |
|
| Bete |
Com as associações da tabela acima, podemos marcar a alternativa D.
Resposta: D (Yara mora no 4º andar e tem um cachorro)
VUNESP – TJ/SP – 2017) Carlos é o único atleta que tem patrocínio de 3 empresas: A, B e C. Em se tratando de atletas que recebem patrocínios de apenas 2 dessas empresas, temos: Leandro e Hamilton, das empresas A e B; Marta e Silas, das empresas A e C; e Amanda, Renata e Sérgio, das empresas B e C. Se esses atletas fazem parte de um grupo contendo, ao todo, 18 atletas que recebem patrocínio das empresas A, B ou C, e cada empresa tem, pelo menos, 1 atleta recebendo patrocínio somente dela, então é correto afirmar que os números mínimo e máximo de atletas que a empresa B pode patrocinar são, respectivamente,
(A) 8 e 16.
(B) 6 e 12.
(C) 4 e 8.
(D) 5 e 10.
(E) 7 e 14.
RESOLUÇÃO:
Veja no diagrama abaixo as informações do enunciado. Note que coloquei 1 pessoa no centro, pois somente Carlos é patrocinado pelas empresas. Coloquei 2 pessoas na interseção apenas entre A e B (Leandro e Hamilton), 2 pessoas na interseção apenas entre A e C (Marta e Silas), e 3 pessoas na interseção apenas entre B e C (Amanda, Renata e Sérgio). Chamei de X, Y e Z as quantidades de pessoas patrocinadas somente por A, B e C, respectivamente.
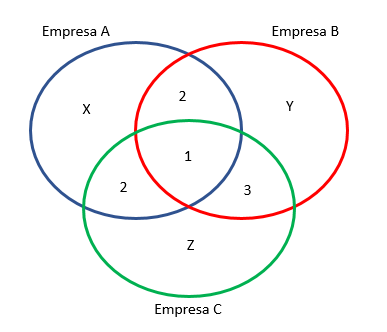
Sabemos que X, Y e Z devem ser, no mínimo, iguais a 1. Isto porque cada empresa tem, pelo menos, 1 atleta recebendo patrocínio somente dela.
Para obter o MAIOR valor possível para Y, devemos considerar que X e Z são os menores possíveis, ou seja, X = 1 e Z = 1. O total de pessoas é 18, logo,
18 = X + 2 + 1 + 2 + Y + 3 + Z
18 = 1 + 2 + 1 + 2 + Y + 3 + 1
18 = 10 + Y
Y= 8
Neste cenário, o número máximo de pessoas patrocinadas pela empresa B é:
2+1+3+Y = 2+1+3+8 = 14
Para obter o mínimo, basta considerar Y = 1, que é o seu menor valor possível. Assim, o número mínimo de pessoas patrocinadas por B é:
2+1+3+1 = 7
Resposta: E (7 e 14)
VUNESP – TJ/SP – 2017) Na sequência numérica 2, 3, 5, 9, 17, 33, 65, 129, …, mantida a ordem preestabelecida, o próximo elemento é
(A) 281.
(B) 273.
(C) 257.
(D) 265.
(E) 249.
RESOLUÇÃO:
Veja que, de um número para o seguinte, estamos somando:
+1, +2, +4, +8, +16, +32, +64…
Estas são as potências de 2. Para chegar no próximo número, devemos pegar o 129 e somar 2×64 = 128, chegando a 129+128 = 257.
Resposta: C (257)
VUNESP – TJ/SP – 2017) Observe as 4 primeiras figuras de uma sequência, em que cada figura contém 5 símbolos:

Nessa sequência, as figuras 5, 6, 7 e 8 correspondem, respectivamente, às figuras 1, 2, 3 e 4, assim como as figuras 9, 10, 11 e 12, e assim por diante, mantendo-se essa correspondência. Com relação à ordem dos símbolos, o 1º dessa sequência é , o 8º é , o 15º é , e assim por diante. Nestas condições, o 189º símbolo é
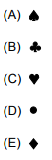
RESOLUÇÃO:
As figuras 1, 2, 3 e 4 possuem, juntas, um total de 20 símbolos. Esta sequência se repete indefinidamente. Para chegar no 189º símbolo, podemos começar dividindo 189 por 20, obtendo o resultado 9 e o resto 9. Isto significa que, para chegar no 189º símbolo, precisamos passar por 9 ciclos completos de 20 símbolos, e pegar o 9º símbolo da sequência seguinte.
O 9º símbolo desta sequência de 20 símbolos é este:

Resposta: A
