Caros alunos,
Vejam abaixo a resolução resumida das questões exigidas no concurso de Auditor da Prefeitura de Juiz de Fora, realizado neste domingo (28/08). Caso discordem de algo, fiquem à vontade para me procurar!
Questão 03 – Um apicultor possui…
Chamando de A e B os conjuntos das colmeias que receberam os venenos A e B, respectivamente, podemos dizer que:
total de colmeias = 400
n(A e B) = 40
n(A) = 200, de modo que n(A – B) = 200 – 40 = 160
n(B) = 130, de modo que n(B – A) = 130 – 40 = 90
Assim, temos 40 colmeias que receberam os DOIS venenos, 160 que receberam APENAS A, e 90 que receberam APENAS B. As colmeias que receberam algum veneno foram, portanto, 40 +160 + 90 = 290.
Como o total é de 400 colmeias, podemos dizer que 400 – 290 = 110 não receberam veneno.
Gabarito A (110).
Questão 04 – Um agrônomo realizou…
Repare que precisamos encontrar o maior número entre 6/11, 2/3 e 4/7. Uma forma de fazer isso com tranquilidade é escrevê-los utilizando o mesmo denominador. Outra forma é escrevendo-os na forma decimal, ou seja, fazendo a divisão.
Veja que 2/3 = 0,666… (esta é uma dízima periódica muito conhecida).
O número 6/11 certamente é INFERIOR a 0,666…, afinal 6/10 é 0,6, de modo que ao dividir 6 por 11 vamos obter um número ainda menor.
O número 4/7 pode ser obtido de forma aproximada. Fazendo a divisão, temos algo como 0,57…
Ou seja, o número 2/3 é o maior. Assim, podemos dizer que a cultura do tipo B teve a maior área infestada.
Gabarito – C (a cultura do tipo B é a que possui a maior área cultivada com infestação da praga)
Questão 05 – Seja a situação na qual…
Veja que a cada acréscimo de 1 unidade em X deveríamos ter um acréscimo de 10 unidades em Y. Isso seria obtido em uma expressão como Y = 10X. Veja que para X = 0 teríamos Y = 0, para X = 1 teríamos Y = 10 (acréscimo de 10 unidades de Y para o acréscimo de 1 unidade de X), para X = 2 teríamos Y = 20 (acréscimo de mais 10 unidades de Y para o acréscimo de mais 1 unidade de X), e assim sucessivamente.
Acontece que NÃO temos essa opção de resposta, motivo pelo qual a questão deve ser anulada.
Gabarito – questão deve ser anulada por falta de gabarito correto.
Questão 06 – No teste da hipótese…
A questão propositalmente não informou o número de graus de liberdade. Neste caso, o examinador queria que você soubesse que a distribuição dada no enunciado (fórmula abaixo) possui distribuição qui-quadrado com (n-1) graus de liberdade: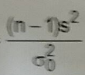
Como vimos na aula 13 do nosso curso, se essa distribuição possui k graus de liberdade, a esperança e a variância são dadas, respectivamente, por:
Esperança = k
Variância = 2k
Se foram usadas n = 15 observações na amostra, então o número de graus de liberdade é k = n-1 = 15-1 = 14.
Assim, temos:
Esperança = k = 14
Variância = 2k = 2.14 = 28.
Gabarito – D (14 e 28)
Seja meu seguidor no INSTAGRAM e acompanhe todas as novidades em primeira mão! Basta clicar na figura:
Saudações,