Artigo

Resumo de Geometria Analítica

No artigo de hoje vamos fazer um resumo de Geometria Analítica!

Resumo de Geometria Analítica

Antes de tudo, você sabe o que é Geometria Analítica?

Geometria Analítica é um ramo da matemática que combina os princípios da geometria com as técnicas da álgebra. Sendo assim, a geometria analítica permite estudar as propriedades geométricas das figuras e objetos utilizando métodos algébricos.

Isto é, a Geometria Analítica busca relacionar a geometria clássica, que lida com pontos, retas, planos e figuras geométricas, com a álgebra, que trata das operações matemáticas envolvendo números e variáveis.

Um dos principais conceitos da Geometria Analítica é a representação de pontos no espaço por meio de coordenadas numéricas. Isso envolve usar sistemas de coordenadas, como o sistema cartesiano, para descrever a posição de pontos, a equação de retas e curvas, e as propriedades geométricas dessas entidades utilizando equações e cálculos algébricos.

Isto posto, a Geometria analítica é a parte da Matemática que relaciona a geometria à álgebra e estuda os resultados da relação. Assim, a Geometria Analítica estabelece conexões entre geometria e álgebra, de maneira que os conceitos da geometria são analisados através de processos algébricos.

Definição de Geometria Analítica

Para entender melhor a geometria analítica, é necessário compreender o que é um plano cartesiano. Desse modo, o plano cartesiano é formado por dois eixos que são perpendiculares entre si, isto é, que formam um ângulo de 90º.

Então, em cada um dos eixos, representamos uma reta numérica com todos os números reais. Nesse sentido, o eixo vertical é conhecido como eixo das ordenadas ou também como eixo y. Por sua vez, o eixo horizontal é conhecido como eixo das abscissas ou eixo x.

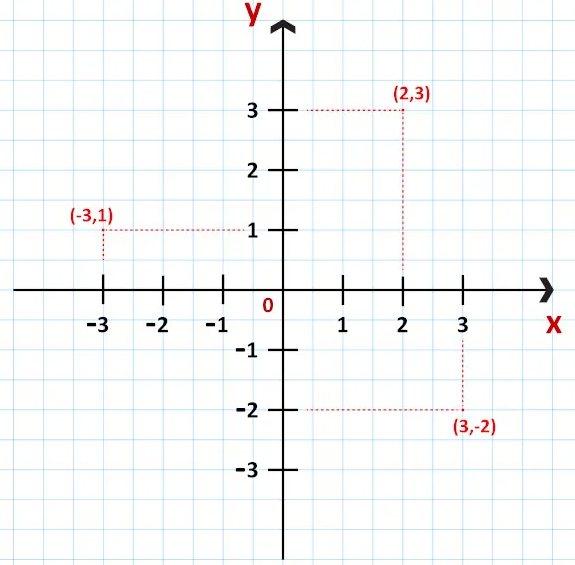
Isto posto, ao representar um objeto no plano cartesiano, é possível extrair informações algébricas do objeto, sendo a primeira e a mais simples, o ponto. Desta forma, todo ponto no plano cartesiano pode ser representado por um par ordenado de acordo com a sua localização em relação a cada um dos eixos.

Representação de pontos no plano cartesiano

Pontos importantes da Geometria Analítica

Alguns pontos importantes que a Geometria Analítica trata, incluem:

Pontos e Coordenadas: Descrição de pontos no espaço através de pares (ou ternas, em espaços tridimensionais) de coordenadas.
Equações de Retas: Representação algébrica de retas no espaço por meio de equações lineares.
Equações de Curvas: Representação algébrica de curvas, como circunferências, elipses, parábolas e hipérboles.
Distâncias e Ângulos: Utilização de técnicas algébricas para calcular distâncias entre pontos e ângulos entre vetores e retas.
Transformações Geométricas: Estudo das transformações que preservam as propriedades geométricas, como translações, rotações e reflexões.
Interseções e Lugares Geométricos: Análise das interseções entre curvas e a determinação dos conjuntos de pontos que satisfazem certas condições geométricas.

Nesse sentido, a base da geometria analítica consiste em representar os pontos de uma reta por meio da utilização dos números reais. Dessarte, cada ponto de uma reta é representado (ou representa um único número real. Ademais, esse número real é obtido pela distância entre o referido ponto e a origem da reta, que é o ponto relacionado com o número zero.

Por sua vez, o conceito de distância, na Geometria Analítica, é um dos mais importantes. Por intermédio dele são definidos outros conceitos que são fundamentais para a Geometria, como os conceitos de circunferência e círculo.

Ademais, a maioria dos conceitos algébricos de figuras geométricas são obtidos por meio do conceito de distância.

Conclusão

Em suma, a Geometria Analítica é uma importante ferramenta matemática que une os princípios geométricos clássicos com as técnicas algébricas modernas. Deste modo, ao permitir a representação numérica de pontos, retas e curvas no espaço, ela nos oferece uma abordagem precisa e eficaz para compreender e manipular as relações geométricas.

Dessa maneira, por meio da Geometria Analítica, somos capazes de resolver problemas complexos em inúmeras disciplinas, desde a física e a engenharia até a ciência da computação e a arquitetura.

Além de suas aplicações práticas, a Geometria Analítica proporciona uma perspectiva abstrata e um conjunto de ferramentas analíticas que ajudam na exploração das formas e estruturas que nos rodeiam. Assim, mediante o ramo da matemática, somos capazes de traduzir problemas geométricos em termos algébricos, facilitando a resolução e a compreensão das propriedades dos objetos geométricos.

Por fim, a Geometria Analítica trata da profunda conexão entre a matemática e o mundo tangível, demonstrando que as ideias abstratas têm aplicações concretas e tangíveis em nossa vida diária. Seja traçando rotas em um mapa, projetando estruturas complexas ou simulando cenários no mundo virtual.

Em resumo, a Geometria Analítica desempenha um papel fundamental na resolução de problemas e na expansão do nosso conhecimento sobre o espaço e suas formas.

Espero que você tenha gostado do nosso artigo de hoje!

Bom Estudo!

Elizabeth Menezes

@prof.elizabethmenezes

https://pt.wikipedia.org/wiki/Geometria_anal%C3%ADtica