Gabarito Extraoficial SEFAZ-CE – Estatística

Oie!!

Como foi a prova da SEFAZ-CE? Gostou?

A seguir, apresento os comentários para as questões 141 a 146. Atente-se aos enunciados, pois a ordem das questões em cada bloco pode ser diferente na sua prova.

Bloco de questões 141 – 143

Suponha que o número diário (X) de transações bancárias registradas em determinada conta bancária se distribua conforme uma distribuição de Poisson. Com respeito ao total semanal de transações bancárias registradas nessa conta bancária, denotada como Y = X₁ + X₂ + X₃ + X₄ + X₅, em que {X₁,…, X₅} representa uma amostra aleatória simples retirada de uma distribuição de Poisson com média igual a 5 transações por dia, julgue os seguintes itens.

Questão 141. O desvio padrão da variável aleatória Y é igual a 5 transações por semana.

Comentários:

O enunciado informa que X segue distribuição de Poisson com média de 5 transações por dia e que Y é a soma de 5 amostras de X. Ou seja, a variável Y representa o número de transações por semana (considerando-se os 5 dias úteis). 

A soma de 5 variáveis com distribuição de Poisson e parâmetro 5 segue distribuição de Poisson com parâmetro:

Em uma distribuição de Poisson, a variância é igual ao parâmetro:

Sabendo que o desvio padrão é a raiz da variância, então o desvio padrão de Y é:

Portanto, o desvio padrão da variável Y é, de fato, igual a 5 transações por semana.

Gabarito preliminar: Certo

Questão 142. 

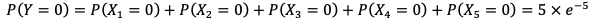
Comentários:

O item pede a probabilidade P(Y = 0) que é a probabilidade de não haver transações em determinada semana. Para isso, é necessário que não haja transações em todos os 5 dias, ou seja, não ter transação no primeiro E não ter transação no segundo e assim até o quinto do dia. Portanto, temos a interseção desses eventos.

A probabilidade da interseção corresponde ao produto das probabilidades, logo:

Assim, concluímos que o item está errado. 

A título de complementação, a probabilidade de não haver transações em determinado dia, sabendo que X segue distribuição de Poisson com parâmetro igual a 5, é dada por:

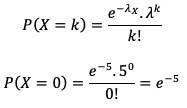
Logo, a probabilidade P(Y = 0) é:

Que é o mesmo resultado que obteríamos ao considerarmos que Y segue distribuição de Poisson com parâmetro igual a 25. 

Gabarito preliminar: Errado

Comentários:

Pelo Teorema Central do Limite, a soma de variáveis aleatórias tende a uma distribuição normal. Logo, Y segue aproximadamente distribuição normal, com média e desvio padrão informados no item.

Para obtermos a distribuição normal padrão Z, utilizamos a seguinte transformação:

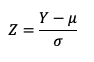
Ou seja, não devemos dividir o desvio padrão de Y pela raiz de 5 e por isso o item está errado.

Gabarito preliminar: Errado

Bloco de questões 144 – 146

Uma amostra aleatória simples de tamanho igual a 4 foi retirada de uma população exponencial cuja função densidade de probabilidade é dada por

Em que A > 0 é o parâmetro desconhecido.

Com base nos valores mostrados no quadro anterior, que constituem uma realização dessa amostra aleatória simples, julgue os itens a seguir.

Questão 144. A estimativa da média populacional obtida pelo critério de mínimos quadrados ordinários é igual a 3.

Comentários:

O estimador de mínimos quadrados para a média populacional é a média amostral:

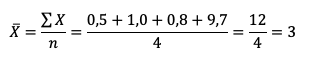
Ou seja, de fato, é igual a 3.

Gabarito preliminar: Certo.

Questão 145. Pelo critério de máxima verossimilhança, a estimativa do parâmetro A é igual a 3.

Comentários:

O estimador de máxima verossimilhança para o parâmetro da distribuição exponencial é o inverso da média amostral (vale lembrar que a distribuição exponencial indica o tempo entre ocorrências):

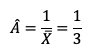
Ou seja, é diferente de 3.

Gabarito preliminar: Errado.

Questão 146. A estimativa de máxima verossimilhança para o desvio padrão populacional é igual a 3.

Comentários:

Em uma distribuição exponencial, o desvio padrão é o inverso do parâmetro (assim como a média da distribuição):

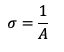
No item anterior, vimos que pela estimativa da máxima verossimilhança para A é Â = 1/3, logo:

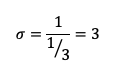
Ou seja, a estimativa para o desvio padrão é, de fato, igual a 3.

Gabarito preliminar: Certo.