Gabarito Raciocínio Lógico e Matemática TJ SP – prova resolvida
Caros alunos, vejam abaixo a resolução das questões de Matemática e Raciocínio Lógico da prova de Escrevente Técnico Judiciário do TJ/SP Interior, bem como o meu gabarito extraoficial.
Espero que aqueles que se dedicaram tenham ido muito bem! PARTICIPEM DO NOSSO RANKING TJ/SP e tenham uma ideia de como vocês estão em relação aos concorrentes! Basta preencher aqui:
RANKING TJ SP ESCREVENTE – PREENCHA AQUI
PROVA DE MATEMÁTICA TJ/SP – GABARITO EXTRAOFICIAL
VUNESP – TJ/SP – 2018) Ontem, os ciclistas Afonso e Bernardo iniciaram os respectivos treinamentos, feitos em uma mesma pista, exatamente no mesmo horário, às 8h 12min. Ambos percorreram a pista no mesmo sentido, sendo que Afonso partiu de um ponto P dessa pista e Bernardo partiu de um ponto Q, situado 1,26 km à frente de P. Por determinação do técnico, no treinamento desse dia, ambos mantiveram ritmos uniformes e constantes: Afonso percorreu 420 metros a cada 1 minuto e 20 segundos, e Bernardo percorreu, a cada 1 minuto e 20 segundos, 80% da distância percorrida por Afonso. Nessas condições, Afonso alcançou Bernardo às
(A) 8h 38min.
(B) 8h 28min.
(C) 8h 30min.
(D) 8h 45min.
(E) 8h 32min.
RESOLUÇÃO:
A cada 1 minuto e 20 segundos, Bernardo percorreu 80% dos 420 metros percorridos por Afonso, ou seja,
Bernardo = 80% x 420 = 8/10 x 420 = 8×42 = 336 metros
Portanto, a cada 1 minuto e 20 segundos (isto é, 80 segundos), a distância entre Afonso e Bernardo diminuía 420 – 336 = 84 metros. Como a distância entre eles era, inicialmente, de 1260m (1,26km), podemos dizer que:
80 segundos ————— 84m
T segundos ————- 1260m
80 x 1260 = 84 x T
T = 1.200 segundos
T = 1.200 / 60 minutos
T = 20 minutos
Logo, se eles começaram às 8:12, eles se encontraram às 8:32, ou seja, 20 minutos depois.
Resposta: E (8h 32min)
VUNESP – TJ/SP – 2018) No posto Alfa, o custo, para o consumidor, de um litro de gasolina é R$ 3,90, e o de um litro de etanol é R$ 2,70. Se o custo de um litro de uma mistura de quantidades determinadas desses dois combustíveis é igual a R$ 3,06, então o número de litros de gasolina necessários para compor 40 litros dessa mistura é igual a
(A) 16.
(B) 12.
(C) 20.
(D) 28.
(E) 24.
RESOLUÇÃO:
Suponha que vamos montar 1 litro de mistura. Se usarmos o volume G de gasolina (em litros), devemos utilizar o volume de 1 – G de álcool (também em litros). O preço de 1 litro da mistura é dado somando-se os preços das partes com gasolina e com álcool, ou seja,
Gx3,90 + (1-G)x2,7 = 3,06
3,9G + 2,7 – 2,7G = 3,06
1,2G = 0,36
G = 0,36/1,2 = 36/120 = 3/10 = 0,30 litro
Ou seja, em 1 litro da mistura, teremos 0,30 litro de gasolina. Em 40 litros da mistura, teremos 0,3 x 40 = 12 litros de gasolina.
Resposta: B (12)
VUNESP – TJ/SP – 2018) Um investidor adquiriu um terreno por R$ 74.000,00. Algum tempo depois, o terreno foi vendido, e o lucro obtido pelo investidor foi igual a 20% do valor da venda. Se esse investidor conceitua lucro como sendo a diferença entre os valores de venda e de compra, então o lucro obtido por ele nessa negociação foi de
(A) R$ 15.870,00.
(B) R$ 14.400,00.
(C) R$ 18.500,00.
(D) R$ 17.760,00.
(E) R$ 16.600,00.
RESOLUÇÃO:
Sendo V o preço de venda, sabemos que o lucro foi de 0,20V, ou seja, 20% do preço de venda. Sabemos também que:
Lucro = Venda – Custo
0,20V = V – 74000
74000 = 0,8V
V = 74000 / 0,8
V = 92500 reais
O lucro foi de 92500 – 74000 = 18.500 reais.
Resposta: C (18.500)
VUNESP – TJ/SP – 2018) Uma concessionária que vai recapear uma faixa de rolamento de uma pista em certa rodovia, em um trecho de x quilômetros, possui uma determinada quantidade y de balizadores refletivos disponíveis para a sinalização desse trecho e, com base nessa quantidade, constatou que, se colocar um número n de balizadores a cada quilômetro, precisará adquirir mais 40 unidades. Porém, se colocar (n – 4) balizadores a cada quilômetro, sobrarão 20 unidades. Se a razão x/y é de 3 para 52, nessa ordem, então a quantidade de balizadores disponíveis para sinalizar o trecho a ser recapeado é igual a
(A) 260.
(B) 350.
(C) 230.
(D) 330.
(E) 280.
RESOLUÇÃO:
Se forem colocados n balizadores a cada quilômetros, serão necessários n.x balizadores. Para isto é preciso adquirir mais 40 balizadores, logo podemos dizer que:
Número de balizadores = n.x – 40
y = n.x – 40
Colocando (n – 4) balizadores por quilômetro, sobram 20 balizadores. Ou seja,
y = (n-4).x + 20
Igualando as duas expressões para y, temos:
n.x – 40 = (n-4).x + 20
n.x – 40 = n.x – 4x + 20
-40 – 20 = -4x
60 = 4x
x = 15
Sabemos que x/y = 3/52, ou seja, 52x = 3y. Então:
52.15 = 3y
52.5 = y
y = 260
Resposta: A (260)
VUNESP – TJ/SP – 2018) Um estabelecimento comercial possui quatro reservatórios de água, sendo três deles de formato cúbico, cujas respectivas arestas têm medidas distintas, em metros, e um com a forma de um paralelepípedo reto retângulo, conforme ilustrado a seguir.
FIGURA
Sabe-se que, quando totalmente cheios, a média aritmética dos volumes de água dos quatro reservatórios é igual a 1,53 m3 , e que a média aritmética dos volumes de água
dos reservatórios cúbicos, somente, é igual a 1,08 m3 . Desse modo, é correto afirmar que a medida da altura do reservatório com a forma de bloco retangular, indicada por h na figura, é igual a
(A) 1,45 m.
(B) 1,35 m.
(C) 1,55 m.
(D) 1,50 m.
(E) 1,40 m.
RESOLUÇÃO:
Sabemos que Soma = Média x quantidade. Assim, a soma dos volumes dos reservatórios cúbicos é dada pela média de seus volumes (1,08) multiplicada pela quantidade (3), isto é,
Soma dos reservatórios cúbicos = 1,08 x 3 = 3,24m3
A soma dos 4 reservatórios juntos é dada pela multiplicação da média (1,53) pela quantidade (4), isto é,
Soma de todos os reservatórios = 1,53 x 4 = 6,12m3
Logo, o volume do reservatório da figura é a diferença entre a soma dos cubos e a soma total, isto é,
Volume da figura = 6,12 – 3,24 = 2,88m3
Este volume é dado pela multiplicação de suas dimensões:
2,88 = 1,6 x 1,2 x h
1,5m = h
Resposta: D (1,50m)
VUNESP – TJ/SP – 2018) Inaugurado em agosto de 2015, o Observatório da Torre Alta da Amazônia (Atto, em inglês) é um projeto binacional Brasil-Alemanha que busca entender o papel da Amazônia no clima do planeta e os efeitos das mudanças climáticas no funcionamento da floresta. Construída numa região de mata preservada, dentro da Reserva de Desenvolvimento Sustentável do Uamatã, a torre Atto tem 325 m de altura e é a maior estrutura de pesquisa desse tipo em florestas tropicais no mundo. (O Estado de S.Paulo, 16.10.2017. Adaptado)
Considere a torre posicionada perpendicularmente ao solo e admita que o cabo ensionado fixado no solo a uma distância de 75 m da base da torre esteja preso à torre em um determinado ponto, cuja altura, em relação ao solo, seja igual a 100 m. Nesse caso, é correto afirmar que o comprimento desse cabo é igual a
(A) 135 m.
(B) 130 m.
(C) 110 m.
(D) 125 m.
(E) 150 m.
RESOLUÇÃO:
Observe que temos um triângulo retângulo com um cateto medindo 75m, o outro medindo 100m (altura). A hipotenusa deste triângulo retângulo é justamente o comprimento do cabo. Para isso, veja que o triângulo 75 – 100 – h é proporcional ao triângulo 3 – 4 – 5, basta multiplicar cada dimensão por 25. Assim,
h = 5 x 25 = 125m
Você também poderia resolver aplicando o teorema de Pitágoras:
h2 = 752 + 1002
Resposta: D (125m)
PROVA DE RACIOCÍNIO LÓGICO TJ/SP – GABARITO EXTRAOFICIAL
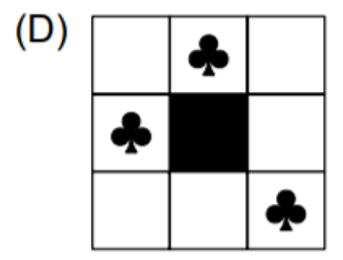
VUNESP – TJ/SP – 2018) Considere os primeiros 8 elementos da sequência de figuras:
FIGURA
Nesta sequência, as figuras 9, 10, 11, 12, 13, 14, 15 e 16 correspondem, respectivamente, às figuras 1, 2, 3, 4, 5, 6, 7, 8, assim como as figuras 17, 18, 19, 20, 21, 22, 23 e 24, e assim segue, mantendo-se esta correspondência. Sobrepondo-se as figuras 109, 131 e 152, obtém-se a
figura…
RESOLUÇÃO:
Observe que temos um ciclo que se repete indefinidamente. Este ciclo é formado por 8 figuras consecutivas em que o quadrado central é pintado de preto, e o símbolo de “paus” vai girando no sentido horário.
Queremos chegar na figura 109. Para isso, basta dividir 109 por 8, obtendo o resultado 13 e o resto 5. Isto significa que a 109ª figura é igual à 5ª figura.
Dividindo 131 por 8, temos resultado 16 e resto 3, de modo que a 131ª figura é igual a 3ª figura.
Dividindo 152 por 8, temos 19, e resto zero. Isto significa que a 152ª figura é igual a 8ª (última do ciclo), pois temos um número exato de ciclos.
Sobrepondo a 5ª, a 3ª e a 8ª figura, temos aquela da alternativa D:
Resposta: D
VUNESP – TJ/SP – 2018) Na sequência numérica 1, 2, 3, 6, 7, 8, 21, 22, 23, 66, 67, 68, …, os termos se sucedem segundo um padrão. Mantido o padrão, o décimo quarto termo é o número
(A) 282.
(B) 202.
(C) 255.
(D) 229.
(E) 308.
RESOLUÇÃO:
Observe que o 4º termo da sequência (6) é a soma dos três anteriores. O 7º termo da sequência (21) também é a soma dos três anteriores. O 10º termo (66) também é a soma dos três anteriores. Assim, o 13º termo deve ser a soma dos três anteriores, ou seja,
13º termo = 66 + 67 + 68 = 201
O 14º termo é o próximo número, ou seja, 202.
Resposta: B (202)
VUNESP – TJ/SP – 2018) Em um grupo de 100 esportistas que praticam apenas os esportes A, B ou C, sabe-se que apenas 12 deles praticam os três esportes. Em se tratando dos esportistas que praticam somente dois desses esportes, sabe-se que o número dos que praticam os esportes A e B é 2 unidades menor que o número dos que praticam os esportes A e C, e o número dos esportistas que praticam B e C excede em 2 unidades o número de esportistas que praticam os esportes A e C. Sabe-se, ainda, que exatamente 26, 14 e 12 esportistas praticam, respectivamente, apenas os esportes A, B e C. Dessa forma, o número total de esportistas que praticam o esporte A é
(A) 62.
(B) 56.
(C) 60.
(D) 54.
(E) 58.
RESOLUÇÃO:
Vamos chamar de AB, AC e BC os esportistas que praticam apenas 2 esportes (designados pelas duas letras). Sabemos que o número dos que praticam os esportes A e B é 2 unidades menor que o número dos que praticam os esportes A e C:
AB = AC – 2
O número dos esportistas que praticam B e C excede em 2 unidades o número de esportistas que praticam os esportes A e C:
BC = AC + 2
Ao todo temos:
– esportistas que fazem os 3 esportes: 12
– esportistas que fazem somente 1 esporte: 26 + 14 + 12 = 52
– esportistas que fazem somente 2 esportes:
AB + AC + BC =
(AC – 2) + AC + (AC + 2) =
3xAC
Como o total de esportistas é igual a 100, então:
100 = 12 + 52 + 3xAC
100 = 64 + 3xAC
36 = 3 x AC
AC = 12
O número de esportistas que praticam A é dado pela soma de:
– esportistas que praticam os 3 esportes: 12
– esportistas que praticam somente A: 26
– esportistas que praticam A e C: AC = 12
– esportistas que praticam A e B: AB = AC – 2 = 12 – 2 = 10
Temos, ao todo, A = 12 + 26 + 12 + 10 = 60.
Resposta: C (60)
VUNESP – TJ/SP – 2018) “Carlos tem apenas 3 irmãs, e essas 3 irmãs cursam o ensino superior.” Supondo verdadeira a afirmação apresentada, é correto afirmar que
(A) se Bia não é irmã de Carlos, então ela não cursa o ensino superior.
(B) se Ana cursa o ensino superior, então ela é irmã de Carlos.
(C) Carlos cursa o ensino superior.
(D) Carlos não cursa o ensino superior.
(E) se Rute não cursa o ensino superior, então ela não é irmã de Carlos.
RESOLUÇÃO:
Vejamos cada opção de resposta:
(A) se Bia não é irmã de Carlos, então ela não cursa o ensino superior.
ERRADO. Pode haver outras mulheres que cursam ensino superior, além das irmãs de Carlos.
(B) se Ana cursa o ensino superior, então ela é irmã de Carlos.
ERRADO, pois nem todas as mulheres que cursam ensino superior são irmãs de Carlos.
(C) Carlos cursa o ensino superior.
ERRADO, não temos qualquer elemento a respeito de Carlos, somente sobre suas irmãs.
(D) Carlos não cursa o ensino superior.
ERRADO, pelo mesmo motivo do item anterior.
(E) se Rute não cursa o ensino superior, então ela não é irmã de Carlos.
CORRETO. Todas as irmãs de Carlos fazem curso superior. Se Rute não faz, não tem como ela ser irmã dele.
Resposta: E (se Rute não cursa o ensino superior, então ela não é irmã de Carlos)
VUNESP – TJ/SP – 2018) Se Maria é bonita, então Carlos é rico. Se Ana é feliz, então José é um herói. Sabe-se que Maria é bonita e Ana não é feliz. Logo, pode-se afirmar corretamente que
(A) José é um herói.
(B) José não é um herói e Carlos é rico.
(C) Carlos não é rico.
(D) Carlos é rico ou José é um herói.
(E) José não é um herói.
RESOLUÇÃO:
Temos as premissas:
P1: Se Maria é bonita, então Carlos é rico.
P2: Se Ana é feliz, então José é um herói.
P3: Maria é bonita e Ana não é feliz.
P3 é uma conjunção que já nos dá duas informações: Maria é bonita, e, além disso, Ana não é feliz. Voltando em P1, como “Maria é bonita” é V, então Carlos é rico precisa ser V também. Em P2, como “Ana é feliz” é F, a proposição já está verdadeira, independentemente do valor lógico de “José é um herói”. Nada podemos concluir sobre José, o que nos permite descartar as opções de resposta A e E.
O gabarito é a alternativa D, pois sabemos que Carlos é rico, e isto é suficiente para deixar a disjunção “Carlos é rico ou José é um herói” verdadeira.
Resposta: D (Carlos é rico ou José é um herói)
VUNESP – TJ/SP – 2018) Quatro amigos, Paulo, João, Fábio e Caio, nasceram em anos distintos, a saber 1970, 1977, 1981 ou 1990, não necessariamente nessa ordem. Cada um exerce, também não necessariamente nessa ordem, uma das profissões entre arquiteto, fotógrafo, engenheiro e advogado. Sabe-se que Paulo não nasceu em 1970, que o arquiteto nasceu antes de Caio e antes do fotógrafo João, que Fábio nasceu antes do advogado, que o advogado não nasceu em 1977 e que o engenheiro, que não é Caio, nasceu em 1981. Sendo assim, é correto afirmar que
(A) Caio é arquiteto.
(B) João nasceu antes de Fábio.
(C) o engenheiro nasceu antes do fotógrafo.
(D) Fábio é advogado.
(E) Paulo nasceu antes de Caio.
RESOLUÇÃO:
Podemos montar a tabela a seguir:
| Nome do amigo | Ano de nascimento | Profissão |
| Paulo | 70, 77, 81 ou 90 | Arquiteto, Fotógrafo, Engenheiro ou Advogado |
| João | 70, 77, 81 ou 90 | Arquiteto, Fotógrafo, Engenheiro ou Advogado |
| Fábio | 70, 77, 81 ou 90 | Arquiteto, Fotógrafo, Engenheiro ou Advogado |
| Caio | 70, 77, 81 ou 90 | Arquiteto, Fotógrafo, Engenheiro ou Advogado |
Vamos cortar as informações mais diretas:
- Paulo não nasceu em 70
- Caio não é o arquiteto (pois o arquiteto nasceu antes dele)
- Caio não nasceu em 70 (pois o arquiteto nasceu antes dele)
- João é o fotógrafo
- João não nasceu em 70 (pois o arquiteto nasceu antes dele)
- Fábio não é o advogado (pois nasceu antes dele)
- Fábio não nasceu em 90 (pois nasceu antes do advogado)
- Caio não é o engenheiro
- Caio não nasceu em 81
Temos:
| Nome do amigo | Ano de nascimento | Profissão |
| Paulo | 77, 81 ou 90 | Arquiteto, Engenheiro ou Advogado |
| João | 77, 81 ou 90 | Fotógrafo |
| Fábio | 70, 77, 81 | Arquiteto, Engenheiro |
| Caio | 77, 90 | Advogado |
Fica claro que o advogado é Caio. Sabemos que o advogado não nasceu em 77, de modo que o advogado Caio nasceu em 90. Com isso:
| Nome do amigo | Ano de nascimento | Profissão |
| Paulo | 77, 81 | Arquiteto, Engenheiro ou Advogado |
| João | 77, 81 | Fotógrafo |
| Fábio | 70, 77, 81 | Arquiteto, Engenheiro |
| Caio | 90 | Advogado |
Como o engenheiro nasceu em 81, e João não pode ser o engenheiro (pois é fotógrafo), então João não pode ter nascido em 81, sobrando para ele 77. Ficamos com:
| Nome do amigo | Ano de nascimento | Profissão |
| Paulo | 81 | Arquiteto, Engenheiro ou Advogado |
| João | 77 | Fotógrafo |
| Fábio | 70, 81 | Arquiteto, Engenheiro |
| Caio | 90 | Advogado |
Fica claro que Paulo é o engenheiro, pois ele nasceu em 81. Assim, Fábio nasceu em 70 e é o arquiteto:
| Nome do amigo | Ano de nascimento | Profissão |
| Paulo | 81 | Engenheiro |
| João | 77 | Fotógrafo |
| Fábio | 70 | Arquiteto |
| Caio | 90 | Advogado |
Sendo assim, é correto afirmar que Paulo nasceu antes de Caio (E).
Resposta: E (Paulo nasceu antes de Caio)
VUNESP – TJ/SP – 2018) Considere falsa a afirmação “Se hoje estudo, então amanhã não trabalho.” Nesse caso, é necessariamente verdade que
(A) Amanhã não trabalho.
(B) Hoje estudo e amanhã trabalho.
(C) Hoje não estudo ou amanhã não trabalho.
(D) Se amanhã trabalho, então hoje não estudo.
(E) Hoje não estudo e amanhã trabalho.
RESOLUÇÃO:
Se a condicional hoje estudo à amanhã não trabalho é Falsa, então a sua negação é verdadeira. A negação de p–>q é dada por “p e não-q”, ou seja:
“Hoje estudo E amanhã TRABALHO”
Resposta: B (Hoje estudo e amanhã trabalho)
VUNESP – TJ/SP – 2018) Uma negação lógica para a afirmação “Se Patrícia não é engenheira, então Maurício é empresário” está contida na alternativa:
(A) Patrícia é engenheira ou Maurício não é empresário.
(B) Patrícia é engenheira e Maurício não é empresário.
(C) Se Patrícia é engenheira, então Maurício não é empresário.
(D) Patrícia não é engenheira e Maurício não é empresário.
(E) Se Maurício não é empresário, então Patrícia é engenheira.
RESOLUÇÃO:
Temos a condicional p–>q na forma:
p = Patrícia não é engenheira
q = Maurício é empresário
A sua negação é dada por “p e não-q”, ou seja:
“Patrícia não é engenheira E Maurício NÃO é empresário”
Resposta: D (Patrícia não é engenheira e Maurício não é empresário.)
VUNESP – TJ/SP – 2018) Considere falsa a afirmação “Hélio é bombeiro e Cláudia é comissária de bordo” e verdadeira a afirmação “Se Hélio é bombeiro, então Cláudia é comissária de bordo”. Nessas condições, é necessariamente verdade que
(A) Hélio não é bombeiro.
(B) Hélio é bombeiro ou Cláudia não é comissária de bordo.
(C) Cláudia não é comissária de bordo.
(D) Hélio é bombeiro.
(E) Cláudia é comissária de bordo.
RESOLUÇÃO:
Como a conjunção é falsa, sabemos que sua negação é verdade:
“Hélio NÃO é bombeiro OU Cláudia NÃO é comissária de bordo”
Além disso, sabemos que a condicional p–>q pode ser reescrita na forma ~q–>~p, isto é:
“Se Claudia não é comissária de bordo, então Hélio não é bombeiro”
Ficamos com duas frases verdadeiras:
“Hélio NÃO é bombeiro OU Cláudia NÃO é comissária de bordo”
“Se Claudia não é comissária de bordo, então Hélio não é bombeiro”
Se for verdade que Claudia não é comissária, a primeira frase será verdadeira. E para a segunda ficar verdadeira, precisamos que Hélio não seja bombeiro.
Se for verdade que Hélio não é bombeiro, as duas frases já são verdadeiras, independentemente do que acontece com Claudia.
Note que, em ambos os casos, precisamos que Hélio não seja bombeiro (sublinhei). Esta é uma conclusão que podemos tirar.
Resposta: A (Hélio não é bombeiro)
VUNESP – TJ/SP – 2018) Considere a afirmação “Marta não atende ao público interno ou Jéssica cuida de processos administrativos”.
Uma afirmação equivalente à afirmação apresentada é:
(A) se Marta não atende ao público interno, então Jéssica não cuida de processos administrativos.
(B) se Jéssica não cuida de processos administrativos, então Marta atende ao público interno.
(C) se Marta atende ao público interno, então Jéssica cuida de processos administrativos.
(D) se Marta não atende ao público interno, então Jéssica cuida de processos administrativos.
(E) se Marta atende ao público interno, então Jéssica não cuida de processos administrativos.
RESOLUÇÃO:
A proposição do enunciado pode ser escrita na forma “~p ou q”, onde:
~p = Marta não atende ao público interno
q = Jéssica cuida de processos administrativos
Sabemos que ~p ou q equivale à condicional p–>q, isto é:
“Se Marta atende ao público interno, então Jéssica cuida de processos administrativos”
Resposta: C (se Marta atende ao público interno, então Jéssica cuida de processos administrativos)