Gabarito extraoficial PM/DF – Resolução da Prova de Matemática e Raciocínio Lógico

Olá pessoal!

Como foram na prova de PM-DF? Você já sabe que aqui no Estratégia nós disponibilizamos a resolução das provas o quanto antes! Veja abaixo as questões de Matemática e Raciocínio Lógico da prova que acabou de ser aplicada hoje, dia 20 de maio de 2018, relativas ao concurso público de admissão ao Curso de Formação de Praças (CFP) com graduação de Soldado Policial Militar da Polícia Militar do Distrito Federal do Quadro de Praças Policiais Militares Combatentes – QPPMC .

E lembre-se de participar do Ranking PMDF (clique aqui).

1. IADES – PM/DF – 2018) Se é verdade que alguns candidatos…

RESOLUÇÃO:

Foi dito que alguns candidatos são preguiçosos e que nenhum filho único é preguiçoso.

Veja o diagrama lógico abaixo:

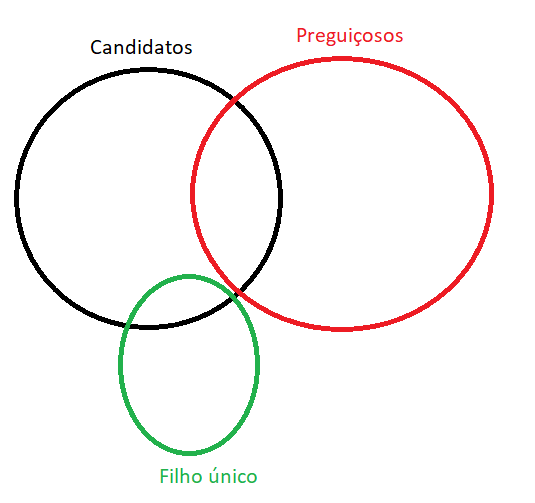
Perceba que nada foi dito em relação a candidatos serem ou não serem filhos únicos. Não temos como concluir nada que relacione apenas candidatos e o fato de ser ou não filho único. Portanto, as alternativas A, B, D e E podem ser descartadas, visto que todas fazem esse tipo de relação.

Só podemos afirmar que algum candidato não é filho único, ou seja, aqueles candidatos que são preguiçosos com certeza não são filhos únicos.

RESPOSTA: C

2. IADES – PM/DF – 2018) Nesse final de semana…

RESOLUÇÃO:

Para que Renato seja um dos dois sorteados, primeiramente é necessário que a bolinha dele não seja a que se perdeu. Para isso, temos uma probabilidade de 39/40. Após isso, para retirar uma duas bolinhas da urna sendo que uma seja a de Renato, temos 38 formas de fazer, visto que temos ao todo 39 bolinhas e queremos garantir que 1 seja a de Renato. Sobram 38 resultados possíveis pra outra bolinha. Assim, os casos favoráveis são 38.

Já o total de casos é dado pela combinação de 39 bolinhas, 2duas a duas –> C(39, 2)

Assim, ficamos com

(39/40) * 38/C(39,2) =

(39/40) * 38/39*38/2 =

(39/40) * 2/39=

2/40 =

= 1/20

RESPOSTA: A

3. IADES – PM/DF – 2018) Para fazer o cadastro… 

RESOLUÇÃO:

Não podemos usar caracteres iguais. Logo, para os números, temos combinação de 10, 2 a 2. Para as letras, temos combinação de 26, 2 a 2. Ao todo, teríamos C(10,2) x C(26,2). No entanto, ainda temos que permutar esses 4 elementos, visto que eles podem aparecer em qualquer posição. Assim, devemos multiplicar o resultado por 4! = 4 x 3 x 2 x 1 = 24. Assim, obtemos:

C(10,2) x C(26,2) x 24 = 45 x 325 x 24 = 351.000

Temos um número maior que 340.000 e menor que 360.000.

RESPOSTA: D

4. IADES – PM/DF – 2018) Uma mistura A… 

RESOLUÇÃO:

Mistura A – proporção 1:2:3
Mistura B – proporção 3:4:5
Queremos saber quanto de clorofórmio teremos em uma terceira mistura. Vamos chamar a terceira mistura de mistura C que é 1L da mistura A e 2L da mistura B.
Para descobrirmos a quantidade de clorofórmio nesta mistura C, vamos calcular quanto desse elemento temos em 1L da mistura A e em 2L da mistura B.
Sabemos pelo enunciado que a proporção é 1 parte de água, para 2 partes de clorofórmio, para 3 partes de benzeno. Portanto, em 1 litro da mistura A temos o total de 6 partes dos elementos e assim podemos calcular a quantidade de cada um:
1 litro ____6 partes
X ___ 1 partes
6 . X = 1 X = 1/6 litros
Sabemos que o clorofórmio significa 2 partes da mistura A, portanto em 1litro teremos 2/6 de clorofórmio.
Na mistura B a proporção é diferente, temos 3 parte de água, para 4 partes de clorofórmio, para 5 partes de benzeno. Portanto, em 2 litros da mistura B temos o total de 12 partes dos elementos e assim podemos calcular a quantidade de cada um:
2 litros _ 12 partes
Y ____ 1 parte
12.Y = 2
Y = 1/6
Sabemos que o clorofórmio significa 4 partes da mistura A, portanto em 2 litros teremos 4/6 de clorofórmio
Assim na mistura C, a quantidade de clorofórmio é a soma da quantidade presente na mistura A somado com a quantidade presente na mistura B. Porém a quantidade total dessa mistura é maior, pois é 1 litro da mistura A mais 2 litros da mistura B, totalizando 3 litros.
Clorofórmio da Mistura C = X +Y
2/ 6 + 4/6 = 6/6 = 1 litro.
Como o enunciado pede a fração de clorofórmio da mistura C, vamos pegar a quantidade desse elemento e dividir pelo volume total desta mistura:
1 litro de clorofórmio / 3 litros de mistura C = 1/3

RESPOSTA: B

5. IADES – PM/DF – 2018) Deseja-se realizar uma festa…

RESOLUÇÃO:

Deseja-se realizar uma festa popular no gramado…
Sabemos que a área disponível tem o formato de um retângulo com medidas de 300m x 500m.
Vamos então calcular a área desse retângulo:
AREA = 300 x 500 = 150.000m2
O enunciado diz que a densidade máxima de é 5 pessoas/m2, como sabemos a área teremos:
DENSIDADE = TOTAL DE PESSOAS / AREA

5 = x / 150.000
TOTAL DE PESSOAS = 750.000

RESPOSTA: Deve ser anulada

Qualquer dúvida poste nos comentários! Abraço!

Prof. Hugo Lima