Gabarito Extraoficial SEFAZ/CE – Matemática e Raciocínio Lógico

Fala, galera! Aqui é o professor Francisco Rebouças e estarei disponibilizando esse Gabarito Extraoficial da prova de Matemática e Raciocínio Lógico da SEFAZ/CE 2021 que ocorreu neste domingo (15/08).

Determinado contribuinte, em débito com a receita estadual, constatou que deve pagar R$ 2.100 para quitar todos os débitos, após desconto concedido por aquele órgão. Após tal desconto, o pagamento pode ser parcelado em até 10 parcelas mensais, sendo a primeira calculada pela razão entre o valor da dívida pós-desconto e o número escolhido de parcelas, paga no momento do acordo. As demais têm seu valor corrigido em 10% em relação à do mês anterior.

Com base nessa situação hipotética, julgue os itens a seguir.

35. Se o valor a ser pago tiver sido resultante de um desconto de 30% sobre a dívida, então o valor da dívida inicial era inferior a R$ 2.800.

Comentários:
Considere que V seja o valor da dívida inicial, sem o desconto. Se com o desconto de 30% o valor a ser pago ficou em R$ 2.100, então podemos escrever que:

Sendo assim, a dívida era de R$ 3.000,00. Como esse valor é superior a R$ 2.800,00, o item está errado.

Gabarito Preliminar: ERRADO.

36. Supondo-se que o contribuinte opte por efetuar o pagamento em 3 parcelas, então a soma algébrica dos valores por ele pagos será inferior a R$ 2.350.

Comentários:
– A primeira parcela é dada pelo valor a ser pago (com o desconto) dividido pelo número de parcelas. Assim,


– A segunda parcela é igual a primeira parcela corrigida em 10%. Nessa situação, corrigir por 10% é a mesma coisa que multiplicar por 1,1. Assim,


– A terceira parcela é igual a segunda parcela corrigida em 10%. Logo,


Pronto, para saber o total pago, devemos somar todas as parcelas encontradas acima.


Como o valor é inferior a R$ 2.350, podemos marcar o gabarito como certo.

Gabarito Preliminar: CERTO.

37. Se o contribuinte optar por parcelar a dívida em n parcelas, 2 ≤n ≤10, conforme previsto no acordo, então a sequência de pagamentos p_1,…,p_n forma uma progressão geométrica, independentemente do valor de n.

Comentários:
Bora lá! A primeira parcela é o valor da dívida (vamos chamar de p_0) dividido pelo número de parcelas. Assim,

A segunda parcela é igual a primeira parcela, corrigida em 10%. Nessa situação, quando corrigimos por 10%, estamos multiplicando a primeira parcela por 1,1. Assim,

Por sua vez, a terceira parcela fica:


A quarta parcela fica:


Observe que a razão entre quaisquer dois termos consecutivos é sempre igual a uma constante (no caso, essa constante é igual a 1,1). Quando isso acontece, dizemos que a sequência em questão é uma progressão geométrica e essa constante passa a ser chamada de razão.

Gabarito Preliminar: CERTO.

Determinada cidade estabeleceu que o valor do IPTU corresponderá a 0,2% do valor do imóvel avaliado no mercado imobiliário.



O imóvel cuja planta é dada na figura precedente está localizado em um bairro dessa cidade, onde o metro quadrado está avaliado em R$ 1.500.

A respeito dessa situação, julgue o próximo item.

38. O valor do IPTU desse imóvel é superior a R$ 1.000.

Comentários:
O primeiro passo dessa questão é calcular a área do imóvel. Nesse intuito, podemos interpretar a figura geométrica do enunciado como sendo formada pela composição de outras duas: um retângulo e um trapézio.

Assim, para determinarmos a área do imóvel, devemos encontrar a área do retângulo I e do trapézio II. Depois disso, basta somarmos as duas para obter a área total da figura. Para começar, vamos observar o seguinte:

O lado esquerdo completo mede “14 m”. No entanto, o lado direito mede apenas “6 m”. Para “completar” o lado direito, está faltando “8 m”. Além disso, como o triângulo retângulo que formamos ali na ponta superior direita é isósceles, podemos concluir que a altura do trapézio também mede 8 metros. Assim,

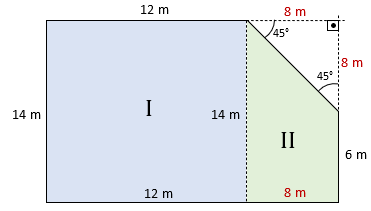
Com todas as medidas em mãos, vamos calcular cada uma das áreas.

A área de um retângulo é dada pelo produto de suas duas dimensões, assim,



Por sua vez, a área II fica assim: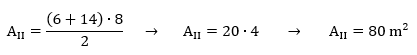



Como a área do imóvel é a soma dessas duas áreas, podemos fazer:



De acordo com o enunciado, o valor do metro quadrado é R$ 1.500. Logo, para encontrarmos o valor do imóvel, devemos multiplicarmos 1.500 pela área total (248 m²).

Pronto, determinamos que o valor do imóvel é R$ 372.000,00. O IPTU é calculado aplicando a alíquota de 0,2% sobre o valor encontrado acima.



Como o valor do IPTU é inferior a R$ 1.000, o item encontra-se ERRADO.

Gabarito Preliminar: ERRADO.

Considere que Marisa, Daniel e Jair trabalhem em uma secretaria de fazenda pública, nos setores responsáveis pela arrecadação do IPTU, IPVA e ISS, que suas idades sejam 34, 42 e 45 anos. Considere, ainda, que não se sabe setor em que cada um deles trabalha nem a idade de cada um. Com base nessas informações, julgue os itens subsequentes.

39. Suponha que, na secretaria da fazenda, a soma do tempo de serviço dos 3 servidores seja igual a 45 anos e a diferença do tempo de serviço entre quaisquer dois deles seja sempre igual a 5 ou 10 anos. Nessa situação, se Marisa começou a trabalhar após Jair e se Daniel começou a trabalhar antes de Jair, então o tempo de serviço de Daniel é de 15 anos.

Comentários:
Vamos chamar de M, J e D os tempos de serviço de Marisa, Jair e Daniel, respectivamente. Como a soma do tempo de serviço dos três servidores é igual a 45 anos, então:



Agora, vamos tentar determinar a ordem de antiguidade no serviço. Se Marisa começou a trabalhar após Jair, então Jair é mais antigo que Marisa.

Jair → Marisa

Como Daniel começou a trabalhar antes de Jair, então Daniel é mais antigo que Jair. Assim,

Daniel → Jair → Marisa

Pronto, essa é a ordem! Daniel é o mais antigo (tem mais tempo de serviço), enquanto Marisa é a mais moderna (com menor tempo de serviço, entre os três). Por que saber disso vai nos ajudar? Vamos ver isso agora!

O enunciado fala que a diferença entre os tempos de serviço entre quaisquer dois deles é 5 ou 10 anos. Para isso acontecer, devemos ter que:

– A diferença de tempo de serviço entre Jair e Marisa é de 5 anos.



– A diferença de tempo de serviço entre Daniel e Jair é de 5 anos também.



– Com isso, a diferença de tempo de serviço entre Daniel e Marisa é de 10 anos.



Professor, a diferença entre o tempo de serviço entre Jair e Marisa não pode ser 10 anos? Não pode pessoal, pois geraria uma diferença entre Daniel e Marisa de 15 anos e a diferença só pode ser 5 ou 10.

Sabendo disso, podemos montar um sistema de equações e resolvê-lo.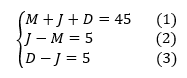



Isolando M em (2):



Substituindo em (1):



Isolando J em (3):



Substituindo em (4):



Logo, o tempo de serviço de Daniel é de 20 anos e não de 15, como aponta o item.

Gabarito Preliminar: ERRADO.

40. Considere as seguintes afirmações.

I. Jair trabalha no setor responsável pelo IPTU.
II. O que trabalha no setor responsável pelo IPVA tem 34 anos de idade.
III. Marisa tem 45 anos de idade ou trabalha no setor responsável pelo IPVA.

É correto afirmar que, se as afirmações I e II são verdadeiras e III é falsa, então a idade de Jair é 45 anos.

Comentários:
Galera, vamos desenhar uma tabela para nos ajudar a organizar as informações.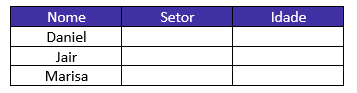



Sabemos que é verdade que Jair trabalha no setor responsável pelo IPTU. Assim,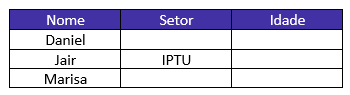



Agora, vamos analisar a afirmativa falsa.

“Marisa tem 45 anos de idade ou trabalha no setor responsável pelo IPVA.”

Ora, se essa afirmativa é falsa, então sua negação é verdadeira.

“Marisa não tem 45 anos de idade e não trabalha no setor responsável pelo IPVA.”

Veja que aqui nós utilizamos uma das leis de Morgan para negar a proposição composta. Com isso, a disjunção vira conjunção e negamos cada uma das proposições simples. Se a afirmativa acima é verdadeira, então podemos concluir corretamente que:

– Marisa não tem 45 anos;
– Marisa não trabalha no setor responsável pelo IPVA.

Se Marisa não trabalha no setor responsável pelo IPVA e já sabemos que Jair trabalha no setor responsável pelo IPTU, então o único setor que “sobra” para Marisa é o setor do ISS.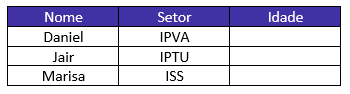



Com isso, o setor do IPVA fica para o Daniel.

Por último, vamos analisar a segunda afirmativa, que sabemos ser verdade.

– O que trabalha no setor responsável pelo IPVA tem 34 anos de idade.

Ora, quem trabalha no setor responsável pelo IPVA é Daniel, logo, é ele que tem 34 anos de idade.



Se Marisa não tem 45 anos e sabemos que Daniel tem 34, a única idade que sobra para ela é 32 anos.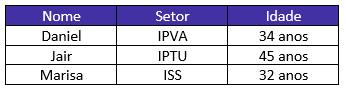



Pronto, se Daniel tem 34 e Marisa tem 32, então a idade de Jair só pode ser 45 anos, conforme aponta o item.

Gabarito Preliminar: CERTO.

Julgue os itens seguintes, considerando a estrutura lógica das situações apresentadas em cada caso.

41. Suponha que 6 servidores participem de uma reunião em uma sala onde algumas cadeiras estejam dispostas em volta de uma mesa circular de modo que a distância entre duas cadeiras consecutivas seja sempre igual a 1 metro. Nesse caso, se os servidores Paulo, Mateus e Rogério se sentaram em cadeiras de modo que a distância de cada um deles aos outros membros do grupo, respeitadas as limitações físicas ao deslocamento, seja sempre maior ou igual a 3 metros, então é correto concluir que a quantidade mínima de cadeiras que formam o círculo é igual a 18.

Comentários:
Pessoal, essa é uma boa questão para tentar sair com um contraexemplo. No entanto, primeiramente vamos tentar entender o problema.

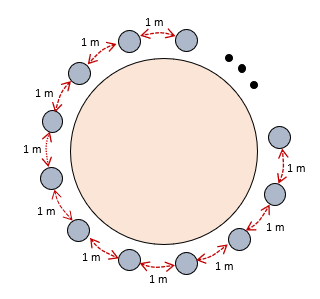
Observe que temos uma mesa circular (maior e representada de marrom) e ao redor dela, cadeiras (que estão representadas pelos círculos menores, em cinza). Cada cadeira está afastada uma da outra de 1 metro. Paulo, Mateus e Rogério se sentam sempre afastados de cada um dos outros membros do grupo, com uma distância maior ou igual a três metros.

Além disso, é importante notar que nada foi falado com relação aos outros três servidores que participam da reunião, de forma que esses outros três podem se sentar em cadeiras vizinhas, distantes de um metro, sem problema algum. Uma situação possível que obedece a todas essas condições seria a seguinte:

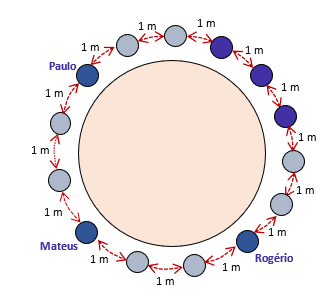
Os 6 servidores estão distribuídos obedecendo as informações que foram passadas pelo enunciado. Apesar disso, apenas 14 cadeiras são utilizadas. Como a questão fala que a quantidade mínima de cadeiras para isso acontecer é 18, o item encontra-se errado.

Gabarito Preliminar: ERRADO.

42. Suponha que a afirmação “Carlos pagará o imposto ou Ana não comprará a casa.” seja falsa. Nesse caso, é correto concluir que Ana comprará a casa.

Comentários:
Se a afirmação do enunciado é falsa, a sua negação será verdadeira.

Como temos uma disjunção, para negá-la, precisaremos usar uma das leis de De Morgan. Simplificadamente, vamos negar cada uma das proposições simples e substituir a disjunção por uma conjunção (trocar o “ou” por “e”). A negação fica:

“Carlos não pagará o imposto e Ana comprará a casa.”

Como sabemos que a afirmação acima é verdadeira e sendo ela uma conjunção, podemos concluir que Ana comprará a casa, de fato.

Gabarito Preliminar: CERTO.