Gabarito Extraoficial PCDF (Escrivão) – Matemática e Raciocínio Lógico
Fala, pessoal!
Sou o Eduardo Mocellin, professor de Matemática e de Raciocínio Lógico do Estratégia Concursos.
Neste artigo, disponibilizo o gabarito extraoficial da disciplina de Matemática e Raciocínio Lógico da prova da PCDF de 2021 para o cargo de Escrivão.
Ressalto que a ordem das questões pode variar de acordo com cada modelo de prova.
Antes de analisarmos as questões, convido você a me seguir no Instagram: @edu.mocellin
Texto para as questões 109 e 110

Questão 109

Gabarito: ERRADO.
Pessoal, creio que a banca exagerou na dose dessa questão. Na hora da prova, a melhor coisa a se fazer seria um chute direcionado ou então deixar a questão em branco. Vamos resolvê-la passo a passo.
1 – Estrutura da senha
Observe que a senha apresentará números conhecidos, 23, 12 e 19, bem como apresentará números desconhecidos, que podem variar de 0 a 9. A estrutura da senha é a seguinte:
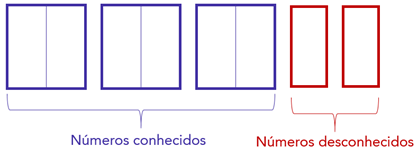
2 – Possibilidades de organização da estrutura da senha
Note que a estrutura da senha pode ser organizada de diversas formas. Uma possibilidade, por exemplo, seria a estrutura abaixo:

O número de possibilidades de organização da estrutura da senha é:
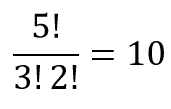
3 – Possibilidades de atribuição dos números conhecidos
Uma vez definida a estrutura da senha, devemos atribuir os números conhecidos à estrutura. Temos três números de dois dígitos para atribuir nas caixas azuis: 23, 12 e 19.
Temos 3 possibilidades para a primeira caixa azul, duas possibilidades para a segunda caixa azul e uma possibilidade restante para a última caixa azul, totalizando:
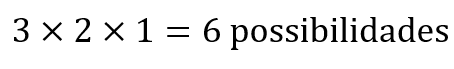
Veja um exemplo em que atribuímos os números conhecidos:

4 – Possibilidades atribuição dos números desconhecidos
Para os números desconhecidos, temos 10 possibilidades para o número à esquerda e 10 possibilidades para o número à direita, totalizando:
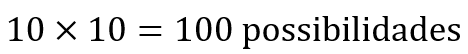
5 – Resultado parcial
Até o momento, o número total de possibilidades de se obter a senha é:

6 – Existem números que foram contabilizados duas vezes dentro das 6.000 possibilidades!!
Pessoal, não temos 6.000 possibilidades de fazer a senha. Observe o seguinte número:
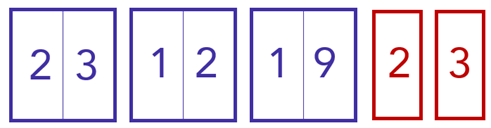
Ele está sendo contado como se fosse diferente do seguinte número:
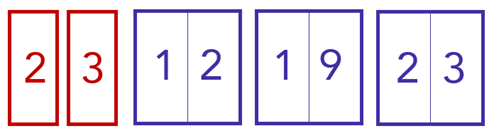
Esses dois números são iguais, pois correspondem a 23121923. Devemos, portanto, remover esses casos em duplicidade.
7 – Estrutura dos números repetidos
Os números repetidos, a princípio, apresentam a seguinte estrutura:
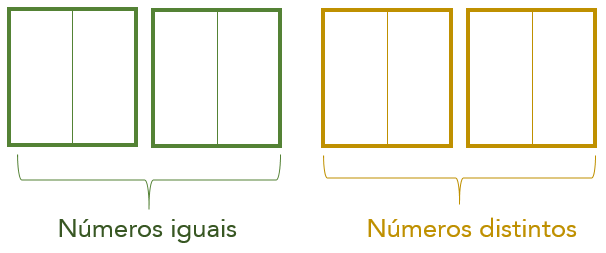
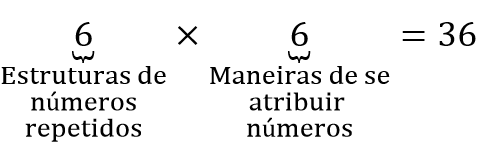
O número de possibilidades de organização da estrutura de número repetidos é:
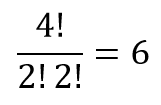
8 – Maneiras de se atribuir números a uma estrutura de números repetidos
Dada uma estrutura de números repetidos, temos 6 maneiras de atribuir números a ela.
Pense comigo: qual desses três números, 23, 12 ou 19, vai se repetir? Temos três possibilidades para isso.
Ainda podemos organizar os 2 números que sobraram, que vão aparecer uma única vez na senha, de duas maneiras: o menor à esquerda e o maior a direita ou o maior à direita e o menor à esquerda.
Portanto, o número de maneiras de se atribuir números a uma estrutura de números repetidos é:
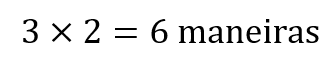
9 – Quantidade de números repetidos
Até o momento, identificamos o seguinte total de números repetidos:
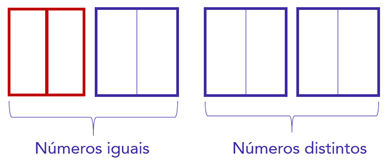
Ocorre que, na nossa estrutura de números repetidos, consideramos apenas os casos em que os dos números desconhecidos estão juntos:
Note que ainda temos outros três casos que foram contabilizados em duplicidade. Nesses três casos, os números desconhecidos não estão sempre juntos:
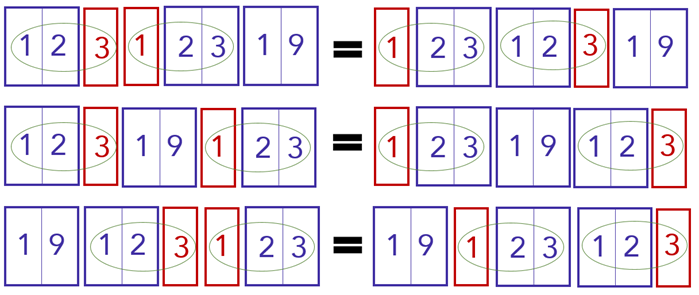
Logo, a quantidade de números repetidos dentro das 6.000 possibilidades é:
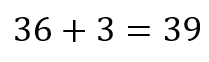
10 – Número de possibilidades de senhas
Portanto, o número de possibilidades de senhas, conhecendo os números 23, 12 e 19, é:
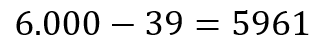
Esse valor é superior a 5.000. O gabarito, portanto, é ERRADO.
Observação
Nessa questão, é possível fazer um “chute direcionado”: ao obter as 6.000 possibilidades, o concurseiro poderia “crer” que o número de casos repetidos dentre esses 6.000 seria diminuto, de modo que, ao descontar esses poucos casos, o número final continuaria superior a 5.000.
Questão 110

Gabarito: CERTO.
Note que, uma vez que desconhecemos a informação de que o dia, o mês e o ano fazem parte da senha, temos 8 casas que podem ser preenchidas por 10 números (de 0 a 9). Nesse caso, pelo Princípio Fundamental da Contagem, temos:
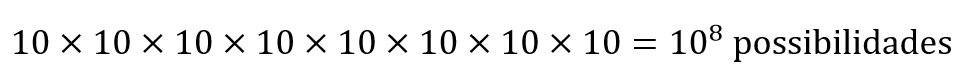
Texto para as questões 111 e 112

Questão 111

Gabarito: CERTO
Sabemos que o número N de candidatos que acertaram o percentual P de questões é dado por:
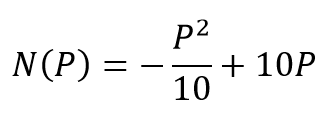
Para um percentual de acerto de 80%, devemos considerar P = 80. Nesse caso, a quantidade de candidatos que acertaram 80% da prova é:
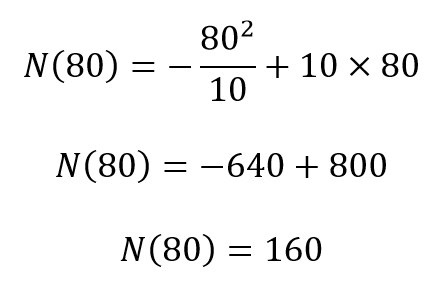
Veja, portanto, que o número obtido corresponde ao número de vagas oferecidas.
Questão 112
Gabarito: ERRADO.
O número de candidatos que compareceram à prova objetiva é:

A concorrência do concurso é dada por:
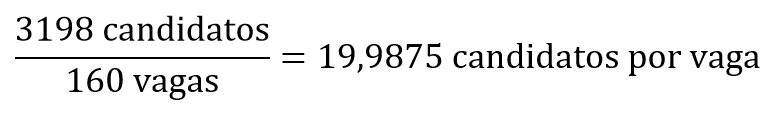
Portanto, a concorrência foi inferior a 20 candidatos por vaga.
Texto para as questões 113 e 114

Questão 113

Gabarito: CERTO.
Note que:
– Na primeira aposta, o jogador gasta R$ 2;
– Na segunda aposta, ele gasta 2 + 2 = 2 × 2 = R$ 4;
– Na terceira aposta, ele gasta 2 + 2 + 2 = 3 × 2 = R$ 6;
– Na quarta aposta, ele gasta 2 + 2 + 2 + 2 = 4 × 2 = R$ 8;
– E assim sucessivamente.
Se considerarmos que cada aposta é um termo de uma Progressão Aritmética, temos que o primeiro termo é a1 = 2 e a razão é r = 2.
Portanto, o termo de ordem n será:
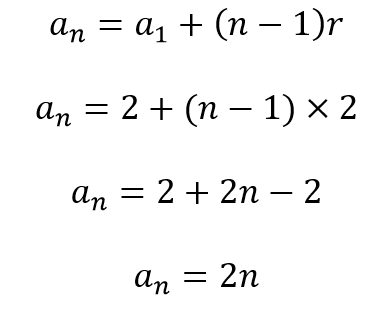
Portanto, na 25ª aposta, o jogador gastará:
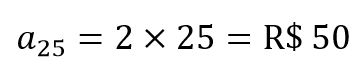
Logo, na 25ª aposta, o jogador aposta o valor máximo permitido.
Questão 114

Gabarito: ERRADO.
Conforme raciocínio da questão anterior, se considerarmos que cada aposta é um termo de uma Progressão Aritmética, temos que o primeiro termo é a1 = 2 e a razão é r = 2.
Note que o valor gasto com a décima aposta é:
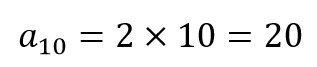
A soma das dez apostas realizadas é:
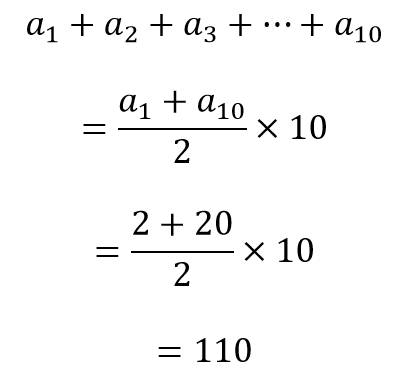
O valor recebido na décima aposta é:
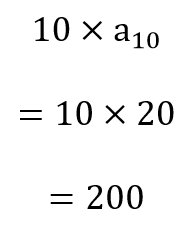
Temos que:
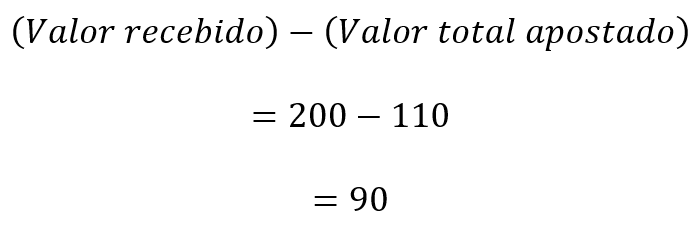
Portanto, o valor do prêmio recebido superou o valor total apostado em R$ 90, valor inferior a R$ 100.
Texto para as questões 115 a 117

Questão 115

Gabarito: ERRADO.
Observe que a proposição categórica é do tipo universal afirmativa (“Todo…”). A sua negação deve gerar uma proposição categórica particular negativa (“Algum…. não”). Portanto, a negação correta da proposição é:
“Alguém não é igual perante a lei”
Em outras palavras, teríamos:
“Alguém é diferente perante a lei”
Questão 116
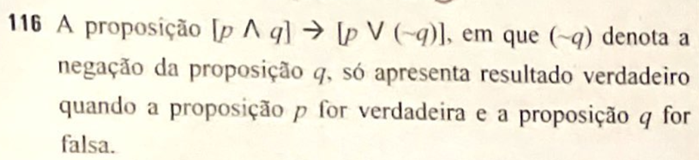
Gabarito: ERRADO.
Para resolver a questão podemos construir a tabela-verdade:
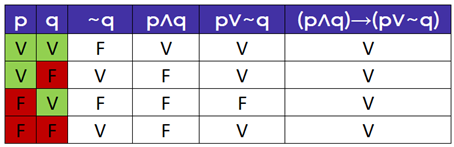
Note que a proposição em questão sempre apresenta resultado verdadeiro para quaisquer combinações de p e de q.
Questão 117

Gabarito: CERTO.
Sejam as proposições simples:
p: “Paulo está mentindo.”
m: “Maria está mentindo.“
A proposição original pode ser descrita por p→~m:
p→~m: “Se [Paulo está mentindo], então [Maria não está mentindo].
Uma equivalência fundamental envolvendo o conectivo condicional é a contrapositiva: p→q ≡ ~q→~p. Para aplicar essa equivalência, devemos realizar o seguinte procedimento:
- Invertem-se as posições do antecedente e do consequente; e
- Negam-se ambos os termos da condicional.
Para o caso em questão, temos:
p→~m ≡ ~(~m)→~p
A dupla negação de uma proposição corresponde à proposição original. Ficamos com:
p→~m ≡ m→~p
A proposição equivalente pode ser descrita por:
m→~p:”Se [Maria está mentindo], então [Paulo não está mentindo].”
Questão 118

Gabarito: ERRADO.
Primeiramente, vamos desconsiderar a restrição de que duas pessoas não podem sentar lado a lado. Nesse caso, o número de possibilidades em que 6 pessoas podem se reunir em uma mesa redonda é a Permutação Circular de 6:
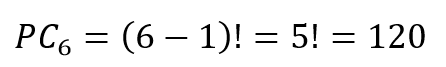
Como duas pessoas não podem sentar lado a lado, temos menos do que 120 possibilidades de distribuir as seis pessoas. Logo, a quantidade de maneiras distintas de essas seis pessoas sentarem em torno da mesa é inferior a 400.
Questão 119

Gabarito: ERRADO.
Vamos verificar as possibilidades de se desenhar os conjuntos A, B e C.
“Os grupos A e C têm elemento em comum”
Nesse caso, devemos representar uma intersecção entre os grupos A e C:
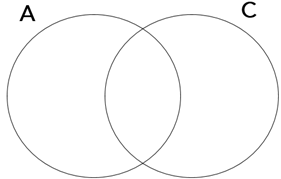
“Todos os indivíduos do grupo B estão no grupo C”
Nesse caso, temos diversas possibilidades de representar todos os indivíduos do grupo B. É necessário somente que todo o grupo B esteja “dentro” do grupo C, incluindo o caso em que o grupo B é igual ao grupo C.
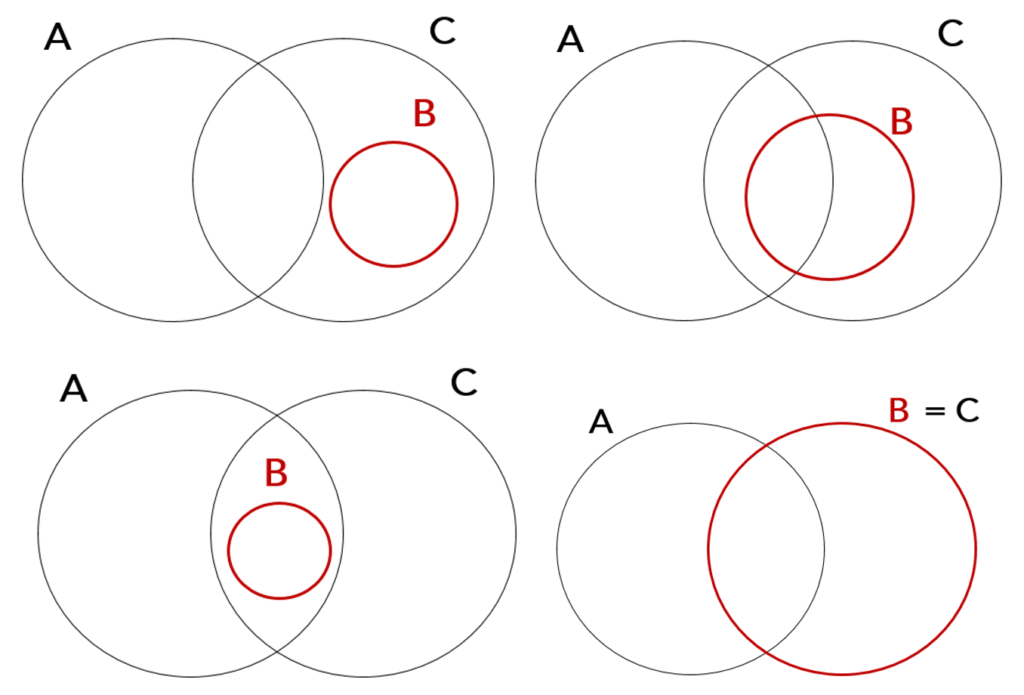
Dessas quatro possibilidades, na primeira não há intersecção entre B e A. Logo, não se pode afirmar que A e B têm algum elemento em comum. O gabarito, portanto, é ERRADO.
Uma possível polêmica que poderia surgir nessa questão ocorreria se o concurseiro supusesse, pela descrição dos grupos, que B e C são iguais. Nessa possível interpretação, apenas o quarto caso seria válido:
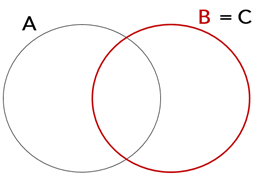
Assim, teríamos necessariamente elementos comuns entre A e B, de modo que o gabarito seria CERTO.
Questão 120

Gabarito: CERTO.
Observe que o número deve ser menor do que 1000 e o algarismo das centenas é igual ao número de diagonais do retângulo. Como o retângulo tem duas diagonais, o número é da seguinte forma:
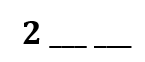
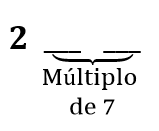
A parte do número formada só pelos algarismos das dezenas e das unidades é múltiplo de 7:
Observe que o número das casas começava em 201 e a casas subsequentes apresentavam a numeração anterior acrescida de 8 unidades. Temos, portanto, as seguintes numerações:
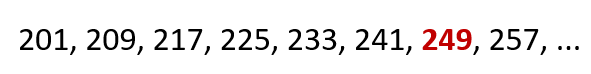
Observe, portanto, que 249 é o número procurado, pois 49 é múltiplo de 7. Logo, o número da casa informado pelo foragido é inferior a 250.
Considerações Finais
Esse é o nosso gabarito extraoficial da disciplina de Matemática e Raciocínio Lógico. Espero que tenham alcançado um bom desempenho. Até a próxima!
Instagram: @edu.mocellin