Gabarito Extraoficial PCDF (Agente): Matemática e Raciocínio Lógico.
Fala, pessoal!
Sou o Eduardo Mocellin, professor de Matemática e de Raciocínio Lógico do Estratégia Concursos.
Neste artigo, disponibilizo o gabarito extraoficial da disciplina de Matemática e Raciocínio Lógico da prova da PCDF de 2021 para o cargo de Agente.
Ressalto que a ordem das questões pode variar de acordo com cada modelo de prova.
Antes de analisarmos as questões, convido você a me seguir no Instagram: @edu.mocellin
Texto para as questões 43 a 46

Antes de resolver a questão, devemos nos atentar para alguns detalhes do enunciado.
Perceba que ocorre uma distinção entre dois tipos de cumprimentos: “apertos de mão” e “acenos“.
Podemos entender que um “aperto de mão“, que ocorre entre rapazes, é recíproco. Isto é, se um rapaz A cumprimenta com um “aperto de mão” um rapaz B, entende-se que esse único “aperto de mão” também corresponde ao “aperto de mão” de B para A.
Por outro lado, podemos entender que um aceno não é recíproco, isto é, se uma moça A acena para uma moça B, esse aceno não corresponde ao aceno de B para A.
Em resumo, partiremos do seguinte entendimento:
- Entre dois rapazes: 1 aperto de mão;
- Entre duas moças: 2 acenos;
- De uma moça para um rapaz: 1 aceno.
Observe que, se o “aceno” fosse recíproco, não haveria sentido dizer que cada moça cumprimentou a todos com um aceno. Isso porque os rapazes não responderiam aos “acenos”, pois eles somente cumprimentam com “apertos de mão” outros rapazes.
Questão 43

Gabarito: CERTO.
Sabemos que cada moça cumprimenta com um aceno outra moça.
Lembre-se que um aceno não é recíproco, isto é, se uma moça A acena para uma moça B, esse aceno não corresponde ao aceno de B para A.
Como temos um total de 20 moças que cumprimentam as outras 19, o número de cumprimentos com acenos entre moças foi:

Portanto, o número de cumprimentos com acenos entre moças foi superior a 200.
Questão 44

Gabarito: CERTO.
Cada uma das 20 moças cumprimenta com um aceno cada um dos 18 rapazes. Logo, o total de acenos entre moças e rapazes foi de:
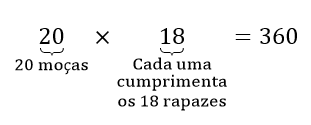
Portanto, o número de cumprimentos entre moças e rapazes com acenos foi superior a 350.
Questão 45

Gabarito: CERTO.
Suponha que temos um total de M moças e R rapazes.
Observe que, entre rapazes e moças, ocorre apenas um aceno das moças para os rapazes. Isso porque, conforme o enunciado, os rapazes cumprimentam apenas os outros rapazes com um “aperto de mão”.
Logo, cada uma das M moças cumprimentam (com um aceno) os R rapazes.

Note, portanto, que o número de cumprimentos entre rapazes e moças é M×R. Logo, esse número é proporcional ao número de rapazes R.
Questão 46

Gabarito: ERRADO.
Considere que temos M moças e R rapazes. O total de cumprimentos corresponde à seguinte soma:
- Acenos de moças para rapazes;
- Acenos entre moças; e
- Apertos de mão entre rapazes.
O total de acenos de moças para rapazes é M×R, pois cada uma das M moças cumprimentam (com um aceno) os R rapazes:
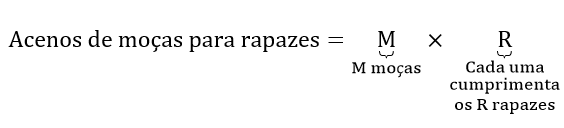
O total de acenos entre moças é M×(M−1), pois cada uma das M moças cumprimentam com um aceno as outras M−1 moças.
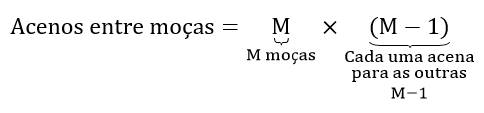
Agora vamos obter o número de cumprimentos com apertos de mão entre rapazes.
Lembre-se que um aperto de mão é recíproco, isto é, se um rapaz A realiza um aperto de mão com um rapaz B, necessariamente esse aperto de mão corresponde ao aperto de B para A.
Caso o aperto de mão não fosse recíproco, teríamos cada um dos R rapazes cumprimentando os outros (R−1) rapazes e, portanto, teríamos R×(R−1) apertos de mão. Ocorre que, como os apertos de mão são recíprocos, estamos contando os apertos em duplicidade, de modo que o total de apertos de mão é:

Outra forma de calcular o número de apertos de mão é pensar que, a cada grupo formado com 2 rapazes, temos um aperto de mão. Portanto, o número de apertos de mão entre R rapazes corresponde a:
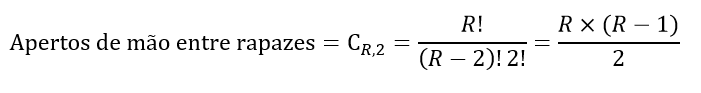
Em resumo, o total de cumprimentos é a seguinte soma:
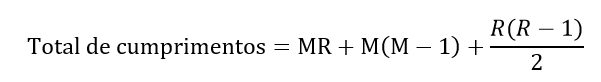
A questão pergunta se esse número é proporcional ao número de pessoas presentes, isto é, proporcional à soma de moças e rapazes (M+R). Essa afirmação é falsa, pois não podemos, na equação acima, colocar em evidência o fator (M+R).
Para mostrar que o total de cumprimentos não é proporcional, vamos usar dois casos particulares.
Considere que temos 2 moças e 2 rapazes, isto é, M = 2 e R = 2. Nesse caso, o total de cumprimentos é:

Note, portanto, que para 4 pessoas (2 moças e 2 rapazes), temos 7 cumprimentos.
Considere agora que temos 4 moças e 4 rapazes, isto é, M = 4 e R = 4. Nesse caso, o total de cumprimentos é:

Note, portanto, que para 8 pessoas (4 moças e 4 rapazes), temos 34 cumprimentos. Veja que dobramos o número de pessoas (de 4 para 8) e, como consequência disso, mais do que dobramos o número de cumprimentos (de 7 para 34). Logo, o número total de cumprimentos não é proporcional ao número de pessoas presentes.
Texto para as questões 47 a 50

Questão 47
Gabarito: CERTO.
Para responder essa questão, devemos lembrar que quando a disjunção inclusiva “ou” é falsa, ambos os termos são falsos. Portanto, como os três que se pronunciaram mentiram nas afirmações, temos:

Isso significa que Marcos, Carlos e Fernando não são culpados. Como exatamente dois são culpados, os amigos que restaram, Luiz e Paulo, são os culpados.
Questão 48

Gabarito: ERRADO.
Sejam as proposições simples:
m: “Marcos é culpado.”
p: “Paulo é culpado.”
c: “Carlos é culpado.”
Dado o contexto da questão, vamos considerar a negação de “é culpado” como “é inocente”. Sabemos que a melhor forma de negar “é culpado” seria utilizar a expressão “não é culpado”. Ocorre que muitas bancas, como o CESPE, costumam ignorar essa sutileza em questões de equivalências lógicas e de lógica de argumentação. Assim, as negações ficam:
~m: “Marcos é inocente.”
~p: “Paulo é inocente.”
~c: “Carlos é inocente.”
Observe que a proposição do enunciado pode ser descrita por m→ ~p ∨ ~c.
m→ ~p ∨ ~c: “Se [Marcos é culpado], então [(Paulo) ou (Carlos são inocentes)].”
Em outras palavras:
m→ ~p ∨ ~c: “Se [Marcos é culpado], então [(Paulo é inocente) ou (Carlos é inocente)].”
Observe que a proposição do enunciado é uma condicional e que a suposta equivalência é uma condicional. Isso significa que devemos utilizar a contrapositiva p→q ≡ ~q→~p. Para aplicar essa equivalência, devemos realizar o seguinte procedimento:
- Invertem-se as posições do antecedente e do consequente; e
- Negam-se ambos os termos da condicional.
Para o caso em questão, temos:
m→ ~p ∨ ~c ≡~ (~p∨~c) → ~m
O antecedente obtido, ~ (~p∨~c), pode ainda ser desenvolvido por De Morgan. Nesse caso, negam-se as duas parcelas e troca-se o “ou” pelo “e”. Temos:
m→ ~p ∨ ~c ≡ ~(~p)∧~(~c) → ~m
A dupla negação corresponde à proposição original. Logo:
m→ ~p ∨ ~c ≡ p∧c → ~m
A condicional acima pode ser expressa por:
p∧c → ~m: “Se [(Paulo é culpado) e (Carlos é culpado)], então [Marcos é inocente].”
A assertiva erra ao não trocar o “ou” pelo “e”. Veja o que foi apresentado:
p∧c → ~m: “Se [(Paulo) ou (Carlos são culpados)], então [Marcos é inocente].”
O gabarito, portanto, é ERRADO.
Questão 49

Gabarito: ERRADO.
Como Carlos nasceu em 1994, a idade dele, considerando que ele já fez aniversário em 2021, é:
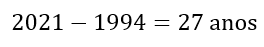
Considere aqui que as idades de Luís, Fernando, Paulo, Carlos e Marcos sejam, respectivamente, L, F, P, C e M.
Assim, temos as seguintes informações:
- Todos eles terão mais de quinze anos de idade:
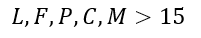
- Carlos nasceu em 1994:
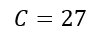
- A diferença de idade entre os dois mais velhos é 10 anos:
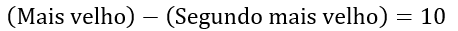
- A soma das idades é igual a 110 anos:
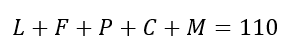
A partir dessas informações, devemos saber se é correto afirmar que, no máximo, dois deles têm dezoito anos de idade ou menos.
Vamos avaliar três possíveis casos:
- Carlos é o mais velho;
- Carlos é o segundo mais velho;
- Carlos não é o primeiro nem o segundo mais velho.
1. Carlos é o mais velho
Sabemos que Carlos tem 27 anos. Nesse caso, como a diferença de idade entre os dois mais velhos é 10 anos, o segundo mais velho terá:
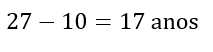
Veja que, nesse caso, não podemos afirmar que “no máximo dois deles têm dezoito anos de idade ou menos”. Isso porque todos os outros suspeitos, exceto Carlos, teriam 17 anos ou menos.
Além disso, tendo o segundo mais velho 17 anos, não teríamos 110 como a soma das idades. Isso porque, mesmo que os demais também tenham 17 anos, a soma daria:
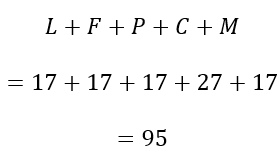
2. Carlos é o segundo mais velho
Nesse caso, o mais velho terá 10 anos a mais do que Carlos. Suponha, arbitrariamente, que Luís seria o mais velho. Nesse caso, temos:
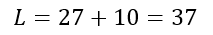
Sabemos que a soma das idades é igual a 110 anos:
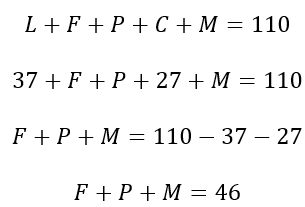
Como todos devem ter mais do que 15 anos de idade, eles devem ter no mínimo 16 anos de idade.
Observe que, mesmo que Fernando, Paulo e Marcos tenham 16 anos, não conseguiremos obter a soma F + P + M = 46, pois 3 × 16 = 48.
Portanto, para esse caso, também não podemos afirmar que “no máximo dois deles têm dezoito anos de idade ou menos”.
3. Carlos não é o primeiro nem o segundo mais velho.
Vamos supor, arbitrariamente, que Luís seja o mais velho e que Fernando seja o segundo mais velho. Nesse caso:
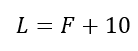
Sabemos que a soma das idades é igual a 110 anos:
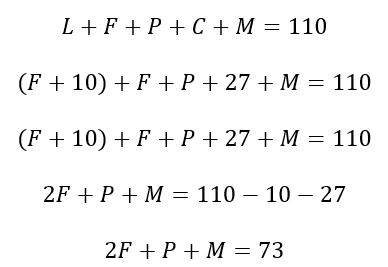
Lembre-se que Fernando é o segundo mais velho e Carlos não é o primeiro nem o segundo mais velho. Se minimizarmos a idade de Fernando, observe que, no pior dos casos, ele terá a idade de Carlos. Nesse caso limite, teremos:
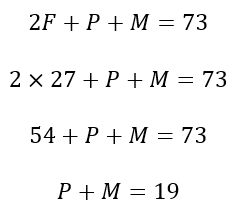
Veja que, mesmo a idade de Fernando sendo a menor possível, Paulo e Marcos não terão mais do que 15 anos, contrariando o enunciado.
Portanto, para esse terceiro e último caso, também não podemos afirmar que “no máximo dois deles têm dezoito anos de idade ou menos”.
Considerações Finais
Esse é o nosso gabarito extraoficial da disciplina de Matemática e Raciocínio Lógico. Espero que tenham alcançado um bom desempenho. Até a próxima!
Instagram: @edu.mocellin