Gabarito Extraoficial e Prova Resolvida – PM SP – Matemática
Olá, pessoal.
Tudo bem?
Aqui quem vos fala é o professor Guilherme Neves.
Vamos agora comentar a prova de Matemática do concurso para PM SP, que foi realizada hoje pela VUNESP.
Aproveito o ensejo para convidá-los a me seguir no instagram @profguilhermeneves e acompanhar dicas e questões comentadas diariamente.
Vamos começar?
- (VUNESP 2018/PM-SP)
Em uma gaveta há 24 canetas, sendo 1/6 delas verdes, 3/8 vermelhas, e as demais azuis. O número de canetas azuis que há nessa gaveta é
(A) 11.
(B) 9.
(C) 7.
(D) 10.
(E) 8.
Resolução
Há um total de 24 canetas.
São (1/6) x 24 = 4 canetas verdes, (3/8) x 24 = 9 canetas vermelhas.
Assim, o total de canetas azuis é 24 – 4 – 9 = 11.
Gabarito: A
- (VUNESP 2018/PM-SP)
Uma pessoa toma 3 medicamentos diferentes: A, B e C. O medicamento A ela toma a cada 4 horas, o medicamento B, a cada 6 horas, e o medicamento C, a cada 12 horas. Sabendo que às 9 horas do dia 1o de agosto essa pessoa tomou os 3 medicamentos juntos, o próximo dia e horário em que essa pessoa tomará esses 3 medicamentos juntos novamente será em
(A) 1º de agosto, às 12 horas.
(B) 2 de agosto, às 12 horas.
(C) 1º de agosto, às 24 horas.
(D) 2 de agosto, às 09 horas.
(E) 1º de agosto, às 21 horas.
Resolução
Questão clássica sobre MMC.
Observe que 12 é múltiplo de 4 e 6. Portanto, mmc(4, 6, 12) = 12.
Desta forma, a pessoa toma os três medicamentos juntos a cada 12 horas.
A pessoa tomou os três medicamentos às 9 horas do dia 1º de agosto. Ela tomará os três remédios juntos 12 horas depois: às 21 horas do dia 1º de agosto.
Gabarito: E
- (VUNESP 2018/PM-SP)
Em certo dia, em uma empresa onde trabalham 36 pessoas, a razão do número de pessoas resfriadas para o número de pessoas não resfriadas era 2/7. No dia seguinte, constatou-se que mais uma dessas pessoas estava resfriada. Assim, a razão do número de pessoas resfriadas para o número de pessoas não resfriadas passou a ser
a) 4/7
b) 1/2
c) 3/7
d) 1/3
e) 1/4
Resolução
A razão do número de pessoas resfriadas para o de não resfriadas é 2/7. Isto quer dizer que podemos dividir o total de pessoas em 9 partes iguais. Duas dessas partes correspondem às pessoas resfriadas e 7 dessas partes correspondem às pessoas não resfriadas.
36/9 = 4.
Portanto, há 2 x 4 = 8 pessoas resfriadas e 7 x 4 = 28 pessoas não resfriadas.
No dia seguinte, há mais uma pessoa resfriada. Assim, haverá 8 + 1 = 9 pessoas resfriadas e 28 – 1 = 27 pessoas não resfriadas.
A razão passou a ser 9/27 = 1/3.
Gabarito: D
- (VUNESP 2018/PM-SP)
No início de um dia, em um escritório, havia 120 envelopes disponíveis para uso, dos quais 37,5% eram amarelos, e os demais, brancos. Sabendo que 20% dos envelopes amarelos e 60% dos envelopes brancos foram utilizados no decorrer do dia, então, o número de envelopes não utilizados nesse dia foi
(A) 64.
(B) 70.
(C) 68.
(D) 62.
(E) 66.
Resolução
O total de envelopes amarelos é 0,375 x 120 = 45.
O total de envelopes brancos é 120 – 45 = 75.
Como 20% dos envelopes amarelos foram utilizados, então 80% dos envelopes amarelos não foram utilizados.
Os envelopes amarelos não utilizados correspondem a 0,80 x 45 = 36.
Sabemos ainda que 60% dos envelopes brancos foram utilizados. Portanto, 40% dos envelopes brancos não foram utilizados. Assim, o total de envelopes brancos não utilizados foi 0,40 x 75 = 30.
O total de envelopes não utilizados foi 36 + 30 = 66.
Gabarito: E
- (VUNESP 2018/PM-SP)
Uma máquina, trabalhando 4 horas por dia, produz um lote de peças em 12 dias. Se essa máquina trabalhasse 6 horas por dia, produziria o mesmo lote de peças em
(A) 8 dias.
(B) 10 dias.
(C) 7 dias.
(D) 6 dias.
(E) 9 dias.
Resolução
A máquina levou 4 x 12 = 48 horas para produzir as peças.
Se trabalhar 6 horas por dia, precisará de 48/6 = 8 dias para concluir o mesmo serviço.
Gabarito: A
- (VUNESP 2018/PM-SP)
Uma pessoa comprou 4 camisetas de valores diferentes, conforme mostra a tabela.
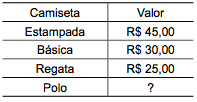
Sabendo que, em média, o valor de cada camiseta foi R$ 40,00, a diferença entre o valor da camiseta mais cara e o da mais barata foi
(A) R$ 35,00.
(B) R$ 20,00.
(C) R$ 30,00.
(D) R$ 15,00.
(E) R$ 25,00.
Resolução
Como a média é R$ 40,00, então o valor total das 4 camisetas é 4 x 40 = 160 reais.
Assim, o valor da camisa polo é 160 – 45 – 30 – 25 = 60 reais.
A camiseta mais cara custou 60 reais. A camiseta mais barata custou 25 reais.
A diferença entre a mais cara e a mais barata foi 60 – 25 = 35 reais.
Gabarito: A
- (VUNESP 2018/PM-SP)
Um estudante precisa fazer todos os exercícios de uma lista e, para isso, decidiu que irá resolver, por dia, sempre a mesma quantidade de exercícios. Se ele resolver 6 exercícios por dia, levará 3 dias a menos do que levaria se resolvesse 4 exercícios por dia. O número de exercícios da lista é
(A) 48.
(B) 60.
(C) 36.
(D) 72.
(E) 12.
Resolução
Digamos que a pessoa leve x dias para resolver todas as questões resolvendo 6 exercícios por dia. Assim, o total de exercícios é 6x.
A pessoa levará (x + 3) dias se resolvesse 4 exercícios por dia. Neste caso, o total de exercícios pode ser calculado como 4(x+3).
Como a quantidade de exercícios é constante, podemos escrever:
6x = 4(x+3)
6x = 4x + 12
2x = 12
x = 6
O total de exercícios é 6 x 6 = 36.
Gabarito: C
- (VUNESP 2018/PM-SP)
Em uma caixa há parafusos e pregos, num total de 20 unidades. Sabendo que há 4 parafusos a mais do que o número de pregos, então, o número de parafusos dessa caixa é
(A) 12.
(B) 4.
(C) 8.
(D) 10.
(E) 6.
Resolução
Seja x o número de pregos. O número de parafusos é x + 4.
Portanto,
x + x + 4 = 20
2x = 16
x = 8.
O total de parafusos é 8 + 4 = 12.
Gabarito: A
- (VUNESP 2018/PM-SP)
Para participar de uma festa são cobrados um ingresso de R$ 80,00 e um preço fixo de R$ 6,00 por qualquer tipo de latinha de bebida. Se uma pessoa gastou nessa festa, com o ingresso e as bebidas, um total de R$ 134,00, então o número de latinhas de bebida consumidas por ela foi
(A) 10.
(B) 8.
(C) 6.
(D) 9.
(E) 7.
Resolução
O total gasto com bebidas foi 134 – 80 = 54 reais.
Como cada bebida custa 6 reais, então ele consumiu 54/6 = 9 latinhas.
Gabarito: D
- (VUNESP 2018/PM-SP)
Um terreno retangular foi dividido em dois lotes, Ι e ΙΙ, conforme mostra a figura, sendo que as medidas indicadas estão em metros.
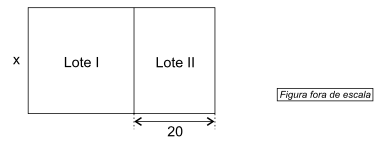
Sabendo que o lote Ι tem a forma de um quadrado com 900 m2 de área, então a área total desse terreno é
(A) 1400 m^2.
(B) 1500 m^2.
(C) 1200 m^2.
(D) 1100 m^2.
(E) 1300 m^2.
Resolução
A área do quadrado é de 900 metros quadrados. Portanto,
x2 = 900
x = 30 metros.
Assim, a altura do retângulo é de 30 metros e a base é de 30 + 20 = 50 metros.
A área total é 30 x 50 = 1.500 metros quadrados.
Gabarito: B
- (VUNESP 2018/PM-SP)
Em uma parede foi colocada uma faixa horizontal com azulejos azuis (A) e azulejos brancos (B), obedecendo à seguinte sequência:
![]()
Mantendo sempre essa mesma ordem na colocação dos azulejos, isto é, um azulejo azul seguido por dois azulejos brancos, e sabendo que essa faixa terá 57 azulejos, então, o número de azulejos brancos dessa faixa será́
(A) 38.
(B) 40.
(C) 42.
(D) 36.
(E) 34.
Resolução
O padrão se repete a cada 3 azulejos. Teremos 57/3 = 19 grupos ABB.
Como em cada grupo há 2 azulejos brancos, então o total de azulejos brancos é 2 x 19 = 38.
Gabarito: A
- (VUNESP 2018/PM-SP)
Um terreno retangular cujas medidas, em metros, estão indicadas na figura, foi totalmente cercado com um muro.
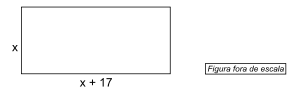
Sabendo que o perímetro desse terreno é 106 metros, então o seu maior lado mede
(A) 31 m.
(B) 22 m.
(C) 27 m.
(D) 18 m.
(E) 35 m.
Resolução
O perímetro é a soma dos lados. Portanto,
x + x + (x + 17) + (x + 17) = 106
4x + 34 = 106
4x = 72
x = 18
O maior lado mede 18 + 17 = 35 metros.
Gabarito: E
Ficamos por aqui.
Um forte abraço,
Guilherme Neves
………………………..
PS: Confira a correção em vídeo do professor Brunno Lima. E não se esqueça de se inscrever no canal do YouTube dele, para receber muito conteúdo gratuito! ;)
nbsp;