Gabarito DEPEN – Raciocínio Lógico (Extraoficial)
Fala, pessoal!
Sou o Eduardo Mocellin, professor de Matemática e de Raciocínio Lógico do Estratégia Concursos.
Neste artigo, disponibilizo o gabarito extraoficial da disciplina de Raciocínio Lógico da prova do DEPEN de 2021 para o cargo de Agente de Execução Penal.
Ressalto que a ordem das questões pode variar de acordo com cada modelo de prova.
Antes de analisarmos as questões, convido você a me seguir no Instagram: @edu.mocellin
Questão 20
Considere as seguintes proposições
p: “Paola é feliz”;
q: “Paola pinta um quadro”.
Assim, a proposição “Paola é feliz apenas se ela pinta um quadro” pode ser representada por ~(p∧~q).
Gabarito: CERTO.
Comentários:
Sabemos que o conectivo “somente se” é do tipo condicional. Esse conectivo difere do “se e somente se“, que é do tipo bicondicional.
Note que a proposição sugerida pelo enunciado é:
“[Paola é feliz] apenas se [ela pinta um quadro]“
O conectivo “apenas se” apresentado na questão corresponde ao condicional “somente se“. Logo, a proposição pode ser descrita por p→q.
Veja que o enunciado sugere que a proposição composta pode ser representada por ~(p∧~q). Podemos desenvolver essa negação por De Morgan. Para negar a conjunção “e”, negam-se ambas as parcelas e troca-se o “e” pelo “ou”. Ficamos com:
~(p∧~q) ≡ ~p ∨ ~(~q)
A dupla negação de uma proposição simples corresponde à proposição original. Logo:
~(p∧~q) ≡ ~p∨q
Nesse momento, você deve se lembrar da equivalência conhecida por “transformação do condicional em disjunção inclusiva“, dada por p→q ≡ ~p∨q.
Conhecendo essa equivalência, observe que ~(p∧~q) é equivalente a ~p∨q que, por sua vez, é equivalente a p→q. Portanto:
~(p∧~q) ≡ p→q
Isso significa que a proposição p→q, “Paola é feliz apenas se ela pinta um quadro”, de fato pode ser representada por sua forma equivalente ~(p∧~q). O gabarito, portanto, é CERTO.
Questão 21
Uma tautologia é uma proposição composta em que seu valor lógico será sempre verdadeiro, independentemente do valor lógico das proposições que a estruturam. Nesse sentido, considerando-se p e q como proposições, a proposição composta p∧q <-> ~(p→~q) é uma tautologia.
Gabarito: CERTO.
Comentários:
A questão pergunta se p∧q <-> ~(p→~q) é uma tautologia. Observe que podemos desenvolver a negação do condicional p→~q presente na segunda parcela do bicondicional.
A negação da condicional é realizada do seguinte modo:
1. Mantém-se o primeiro termo;
2. Troca-se a condicional (→) pela conjunção (∧); e
3. Nega-se o segundo termo.
Para o caso em questão, temos:
~(p→~q) ≡ p∧~(~q)
A dupla negação de uma proposição simples corresponde à proposição original. Logo:
~(p→~q) ≡ p∧q
Observe, portanto, que a bicondicional p∧q <-> ~(p→~q) pode ser descrita por:
p∧q <-> p∧q
Note que temos uma bicondicional composta por duas parcelas iguais. Isso significa que a bicondicional apresenta duas parcelas que sempre terão o mesmo valor lógico. Se p∧q for verdadeiro, temos a bicondicional V<->V, que é verdadeira. Se p∧q for falso, temos a bicondicional F<->F, que também é verdadeira.
Trata-se, portanto, de uma bicondicional sempre verdadeira. Logo, estamos diante de uma tautologia. O gabarito, portanto, é CERTO.
Texto para as questões 22, 23 e 24
Cada um dos itens a seguir apresenta uma situação hipotética, seguida de uma assertiva a ser julgada, com relação a raciocínio lógico.
Questão 22
Em um tabuleiro que possui quatro linhas e cinco colunas, serão distribuídas vinte fichas, numeradas de 1 a 20. Nessa situação, é possível distribuir as fichas no tabuleiro de maneira que a soma dos números das fichas em cada uma das linhas seja sempre a mesma.
Gabarito: ERRADO.
Comentários:
A seguir, temos um tabuleiro com quatro linhas e cinco colunas.
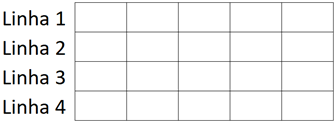
A questão pergunta se, ao distribuir fichas de 1 a 20 nesse tabuleiro, é possível que a soma dos números das fichas em cada uma das quatro linhas seja sempre a mesma.
Note que, ao somar o valor de todas as fichas, temos:
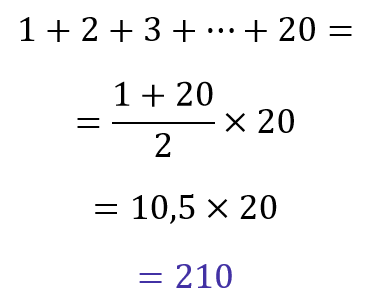
Supondo que é possível fazer com que a soma dos números das fichas em cada uma das quatro linhas seja sempre a mesma, a soma de cada linha seria:
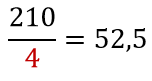
Note que todas as fichas apresentam números inteiros, de modo que é impossível que a soma das fichas de uma determinada linha seja 52,5. O gabarito, portanto, é ERRADO.
Questão 23
Em uma pesquisa, perguntou-se a um grupo de pessoas o seguinte: “você está feliz com o seu trabalho atual?”. Foram admitidos como resposta a esse questionamento apenas “sim” ou “não”, e cada entrevistado emitiu somente uma única resposta. Verificou-se que, no conjunto de respostas obtidas, a quantidade de respostas “sim” foi igual a 50% da quantidade de respostas “não”. Nessa situação, conclui-se que a quantidade de respostas “não” foi superior a 60% do total de respostas obtidas.
Gabarito: CERTO.
Comentários:
Considere que a quantidade de respostas “sim” é S, a quantidade de respostas “não” é N, e o total de respostas é T.
O total de respostas corresponde às respostas “sim” e “não“. Logo:
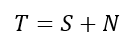
Temos que a quantidade de respostas “sim” foi igual a 50% da quantidade de respostas “não“. Logo:
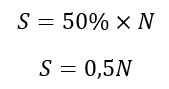
Substituindo S = 0,5N em T = S + N, temos:
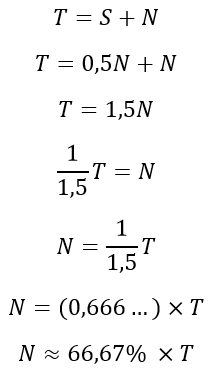
Note que quantidade de respostas “não” foi superior a 60% do total de respostas obtidas. O gabarito, portanto, é CERTO.
Questão 24
A construtora Gama é capaz de construir uma estrada que ligue as cidades A e B no prazo de 15 meses, e a construtora Delta é capaz de construir essa mesma estrada no prazo de 25 meses. Nessa situação, se as duas construtoras forem contratadas para construir a estrada nos respectivos prazos, de modo que a construtora Gama comece a construí-la a partir da cidade A e a construtora Delta comece a construí-la a partir da cidade B, serão necessários mais de 10 meses para concluir a construção da estrada.
Gabarito: ERRADO.
Comentários:
Considere que o comprimento da estrada que deve ser construída é L.
A construtora Gama constrói a estrada de comprimento L em 15 meses. Logo, em um mês, a construtora Gama constrói:
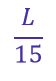
A construtora Delta constrói a estrada de comprimento L em 25 meses. Logo, em um mês, a construtora Delta constrói:
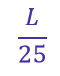
Se ambas as construtoras trabalharem juntas, elas constroem, em um mês:
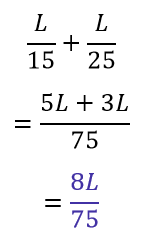
Perceba que, em um mês, elas constroem juntas 8L/75.
Em quanto tempo elas constroem a totalidade da estrada (L)? Para responder à pergunta, podemos resolver por “regra de três”:
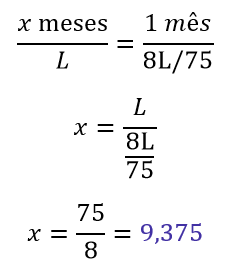
Portanto, as construtoras constroem a estrada juntas em 9,375 meses, valor inferior a 10 meses. O gabarito, portanto, é ERRADO.
Considerações Finais
Esse é o nosso gabarito extraoficial da disciplina de Raciocínio Lógico. Espero que tenham alcançado um bom desempenho. Até a próxima!
Instagram: @edu.mocellin