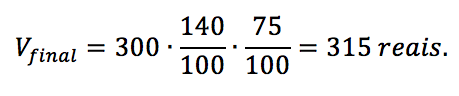Neste artigo, nosso objetivo é fazer com que você conheça todos os modelos de exercícios de porcentagem e acerte todas as questões desse assuntos em provas e concursos.
Para conhecermos os diferentes tipos de exercícios de porcentagem com os quais você poderá se deparar, vamos relembrar alguns pontos importantes da teoria.
Porcentagem é uma razão (fração) de denominador 100. Essas razões de denominador 100 também são chamadas de taxas percentuais ou razões centesimais.
Assim, de uma forma geral, qualquer fração do tipo x/100 pode ser reescrita como x%.
Exemplos:
40/100 = 40%
27/100 = 27%
100/100 = 100%
Dessa forma, sempre que você se deparar com o símbolo %, você pode simplesmente trocá-lo por uma fração de denominador 100.
37% = 37/100
48% = 48/100
Isso é muito importante em exercícios de porcentagem, pois podemos concluir que para calcular x% de um valor, basta multiplicar o valor pelo número x/100.
Exemplo: Calcular 40% de 200
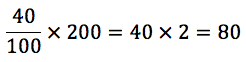
Mesmo com esse conceito tão simples, você já é capaz de resolver muitos exercícios de porcentagem de concursos. Vejamos alguns.
(VUNESP 2017/CM de Sumaré) Para ser aprovado, certo projeto de lei precisa que dos 300 parlamentares, no mínimo 51% votem sim. No dia da votação, 150 parlamentares votaram sim. Nesse caso,
a) faltaram apenas 2 votos para o projeto ser aprovado.
b) faltaram apenas 3 votos para o projeto ser aprovado.
c) o projeto foi aprovado com 3 votos a mais do que o mínimo necessário.
d) o projeto foi aprovado com 5 votos a mais do que o mínimo necessário.
e) o projeto foi aprovado com exatamente 51% de votos sim.
Resolução
Vamos calcular 51% do total de parlamentares.
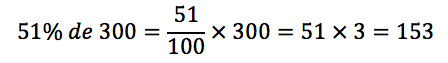
Assim, 153 é o número mínimo de votos para que o projeto seja aprovado.
Portanto, faltaram 3 votos para o projeto ser aprovado.
Gabarito: B
(FGV 2018/BANESTES) Após fazer 80 arremessos à cesta, Marcelinho constatou que acertou 70% deles. Após fazer mais 20 arremessos, ele melhorou seu percentual de acertos para 71% do total de arremessos. Dos últimos 20 arremessos, Marcelinho errou apenas:
a) 6;
b) 5;
c) 4;
d) 3;
e) 2.
Resolução
Marcelinho acertou 70% dos 80 arremessos. O primeiro passo para resolver esse exercício de porcentagem é calcular 70% de 80.
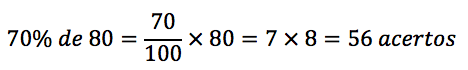
A quantidade de erros foi 80 – 56 = 24.
Após fazer mais 20 arremessos, ele melhorou seu percentual de acertos para 71% do total de arremessos.
Assim, o total de arremessos será 80 + 20 = 100. Portanto, no final, Marcelinho terá acertado 71 arremessos. Consequentemente, o número total de erros ao final terá sido de 100 – 71 = 29.
Como ele havia errado 24 erros inicialmente e no final este número subiu para 29, ele errou 5 arremessos dos 20 arremessos finais.
Gabarito: B
(IBFC 2018/Pref. de Divinópolis) Numa comunidade com 320 pessoas sabe-se que 25% são idosos e 40% são crianças. Nessas condições o total de idosos e crianças dessa comunidade é:
a) 128
b) 112
c) 168
d) 208
Resolução
Os idosos e as crianças juntos representam 25% + 40% = 65% do total. Assim, basta calcular 65% de 320.
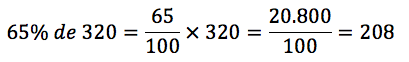
Gabarito: D
(FCC 2018/SABESP) A prefeitura de uma cidade anuncia que, no ano de 2017, recapeou 60% das avenidas da cidade e se compromete a recapear, em 2018, 80% das avenidas restantes. De 2017 para 2018, a quantidade de avenidas dessa cidade não se alterou. Sendo assim, em 2018, do total de avenidas da cidade, a prefeitura deverá recapear:
(A) 80%.
(B) 32%.
(C) 56%.
(D) 42%.
(E) 20%.
Resolução
Suponha que são 100 avenidas. Já foram recapeadas 60 delas. Sobraram 40 avenidas. A prefeitura deverá recapear 80% das 40 restantes.
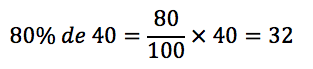
Como o total de avenidas é 100, então este valor representa 32% do total.
Gabarito: B
Outro tópico frequente nos exercícios de porcentagem é a “participação percentual”.
Em outras palavras, nos próximos exercícios de porcentagem, você precisará calcular o quanto uma parte representa do todo em porcentagem.
Exemplo: Imagine que, em um teatro, há 500 pessoas das quais 350 são mulheres. Para calcular a participação percentual das mulheres, basta dividir a quantidade de mulheres pelo total de pessoas.
350/500
Guilherme, como eu faço para escrever tal fração em porcentagem?
É muito simples: para transformar qualquer número em porcentagem, basta que você multiplique o resultado por 100%. Isso é bastante comum não apenas em exercícios de porcentagem, mas também em questões envolvendo taxas de juros em Matemática Financeira.
Pois bem, vamos multiplicar a fração por 100%.
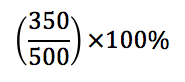
Ao efetuar o produto, vamos simplificar 500 com 100.
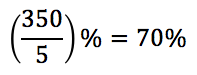
Logo, as mulheres representam 70% das pessoas no teatro.
De uma forma geral, nos exercícios de porcentagem, para calcular a participação percentual de uma parte em relação ao todo, basta dividir a parte pelo todo e multiplicar o resultado por 100%.
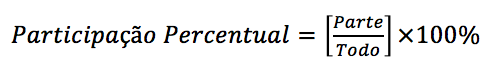
Vamos resolver alguns exercícios de porcentagem envolvendo participação percentual?
(FCC 2019/BANRISUL) Uma papelaria vende cadernos de dois tamanhos: pequenos e grandes. Esses cadernos podem ser verdes ou vermelhos. No estoque da papelaria, há 155 cadernos, dos quais 82 são vermelhos e 85 são pequenos. Sabendo que 33 dos cadernos em estoque são pequenos e vermelhos, a porcentagem dos cadernos grandes que são verdes é
(A) 25%.
(B) 30%.
(C) 15%.
(D) 20%.
(E) 35%.
Resolução
Vamos fazer uma tabelinha para organizar os dados. Sabemos que são 155 cadernos, dos quais 82 são vermelhos e 85 são pequenos.
Assim, podemos concluir que são 155 – 85 = 70 grandes e 155 – 82 = 73 verdes.
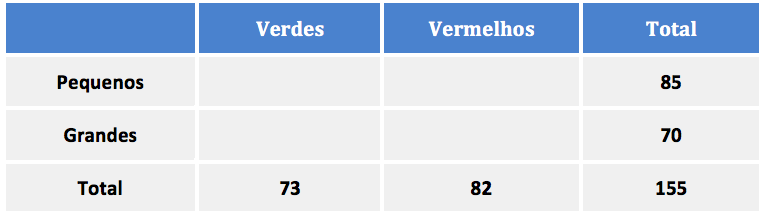
Sabemos que 33 cadernos são pequenos e vermelhos.
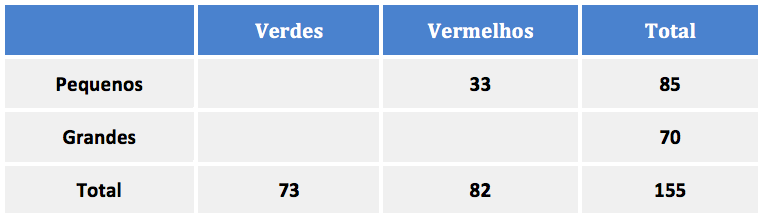
Queremos calcular os cadernos grandes e verdes.
São 85 cadernos pequenos. Como são 33 vermelhos, então são 85 – 33 = 52 verdes.
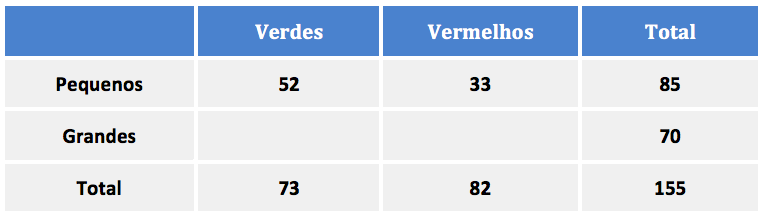
O total de cadernos verdes é 73. Como são 52 pequenos, então são 73 – 52 = 21 grandes.
A questão pergunta: dos cadernos grandes, quantos por cento são verdes?
Dos 70 cadernos grandes, 21 são verdes. Para calcular a porcentagem, basta dividir a parte pelo todo.
21/70 = 0,30 = 30%
Gabarito: B
(VUNESP 2018/CM 2 CÓRREGOS ) Para assistir a uma palestra, estão presentes no auditório 65 homens e 85 mulheres. Sabendo-se que 40% dos homens e 60% das mulheres fazem anotações sobre o que está sendo dito pelo palestrante, então, em relação ao número total de pessoas presentes no auditório, aqueles que não fazem anotações representam, aproximadamente,
a) 48,7%
b) 50,6%
c) 52,5%
d) 54,3%
e) 56,4%
Resolução
Sabemos que 40% dos homens e 60% das mulheres fazem anotações. Portanto, 60% dos homens e 40% das mulheres NÃO fazem anotações.
O total de pessoas que não fazem anotações é:
60% dos homens + 40% das mulheres =
= 0,60 * 65 + 0,40* 85
= 73
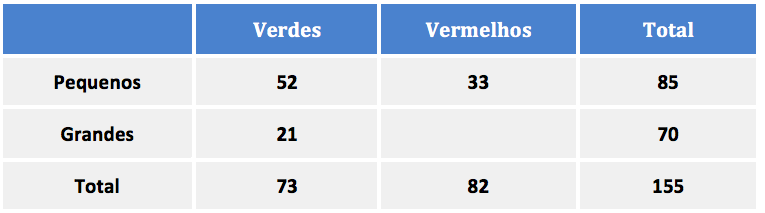
Há 73 pessoas que não fazem anotações. Queremos saber o qual o percentual dessas pessoas em relação ao total. Basta dividir a parte pelo todo e multiplicar por 100%. O total de pessoas é 65 + 85 = 150.
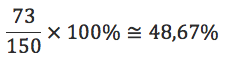
Gabarito: A
(VUNESP 2018/SME BARRETOS ) Levantamento efetuado pela Secretaria de Educação de certo município mostrou que atos de violência física ou psicológica, intencionais e repetitivos (bullying), estiveram envolvidos em cinco de cada oito desavenças entre alunos ocorridas em determinado período.
Com base nessas informações, é correto afirmar que as desavenças não motivadas por bullying representam, do número total de desavenças ocorridas nesse período,
a) 62,5%
b) 60%
c) 40%
d) 37,5%
e) 26,5%
Resolução
Para calcular o percentual, basta dividir a parte pelo todo e multiplicar o resultado por 100%.
O percentual das desavenças motivadas por bullying é:
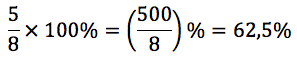
Assim, o percentual das desavenças não motivadas por bullying é:
100% – 62,5% = 37,5%
Gabarito: D
(VUNESP 2018/Prefeitura de Mogi Cruzes) Uma empresa selecionou 160 candidatos para uma entrevista, visando o preenchimento de algumas vagas. Dos candidatos selecionados, 5% não compareceram à entrevista, e 25% dos que compareceram foram contratados. Em relação ao número inicial de candidatos selecionados, aqueles que foram contratados representam
a) 24,25%.
b) 23,75%.
c) 23,25%.
d) 22,50%.
e) 22,25%.
Resolução
Como 5% não compareceram, então 95% compareceram. Vamos calcular 95% do total.
95% de 160 = 0,95 * 160 = 152 compareceram à entrevista
Dos 152 que compareceram, 25% foram contratados. Vamos calcular 25% de 152.
25% de 152 = 0,25 * 152 = 38
Para fazer o cálculo acima mais rápido, basta lembrar que 25% = 1/4. Assim, 25% de 152 = 152/4 = 38.
Dos 160 candidatos, 38 foram contratados. Para calcular a porcentagem de contratados em relação ao total, basta dividir a parte pelo todo e multiplicar o resultado por 100%.
Gabarito: B
(FGV 2015/TJ-SC) Um grupo de amigos se reuniu para as comemorações de fim de ano, sendo que 40% do total eram mulheres. Todos eram torcedores do Figueirense, do Avaí ou do Joinville. Do total, 50% deles eram torcedores do Figueirense.
Metade dos torcedores do Avaí eram mulheres, bem como um quarto dos torcedores do Joinville. Entre os homens, o número de torcedores do Avaí era igual ao número de torcedores do Joinville.
Do total de amigos, eram mulheres torcedoras do Figueirense:
a) 5%;
b)
10%;
c) 15%;
d) 20%;
e) 25%.
Resolução
Vamos construir uma tabela para armazenar os dados.
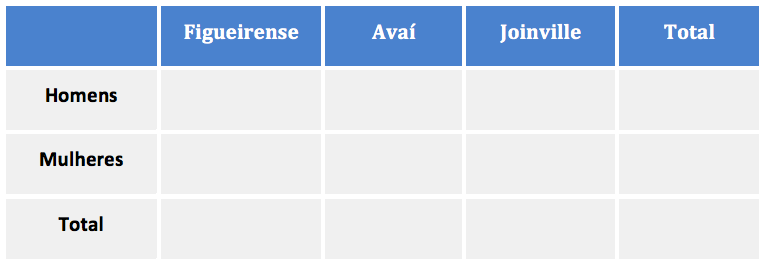
Normalmente atribuímos um valor qualquer ao total de pessoas para resolver uma questão como esta. Entretanto, as informações dadas no enunciado não são favoráveis para resolver a questão desta maneira.
Sabemos que 1/4 dos torcedores do Joinville eram mulheres. Vamos supor que são 10 mulheres torcedoras do Joinville. Desta forma, são 40 torcedores do Joinville (entre homens e mulheres). Como são 10 mulheres, temos 30 homens torcedores do Joinville.
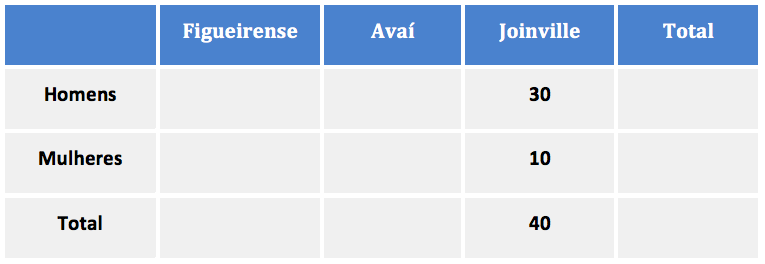
Sabemos ainda que entre os homens, o número de torcedores do Avaí era igual ao número de torcedores do Joinville. Como são 30 homens torcedores do Joinville, teremos também 30 homens torcedores do Avaí.
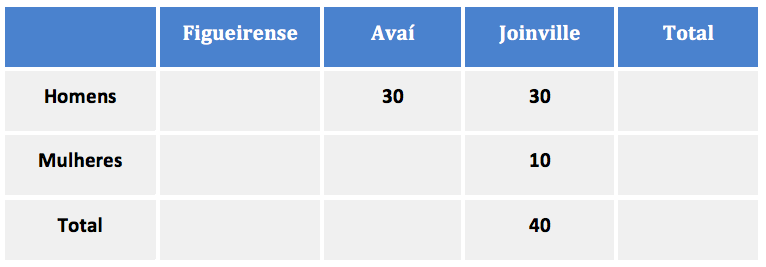
Metade dos torcedores do Avaí eram mulheres. Assim, a outra metade é formada por homens. Como são 30 homens torcedores do Avaí, teremos 30 mulheres torcedoras do Avaí.
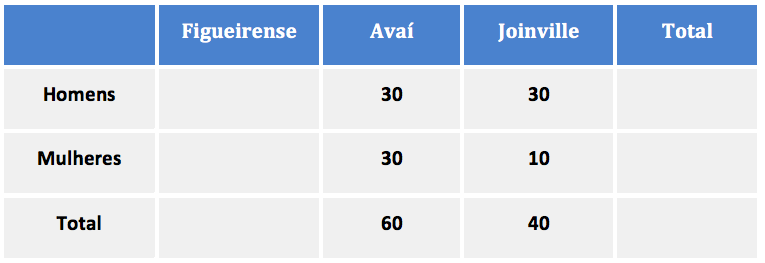
Até agora temos 60 + 40 = 100 pessoas que torcem pelo Avaí ou Joinville.
O enunciado nos diz que 50% do total eram torcedores do Figueirense. Assim, há 100 torcedores do Figueirense e o total de pessoas será igual a 200.
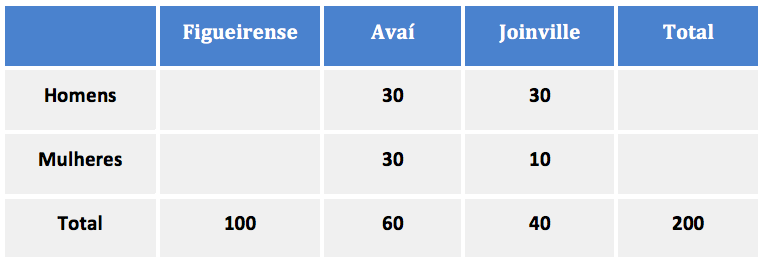
Do total, 40% são mulheres. Como são 200 pessoas, então há 0,40 x 200 = 80 mulheres e 200 – 80 = 120 homens.
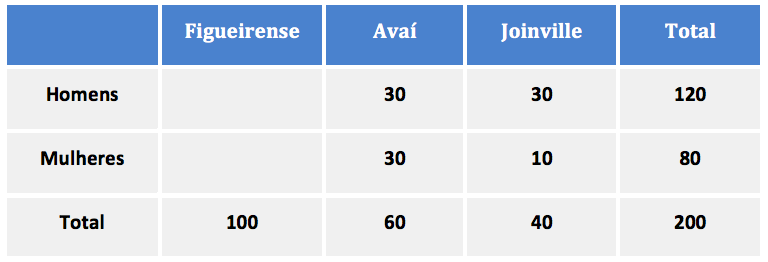
São 120 homens sendo que 30 torcem pelo Avaí e 30 pelo Joinville. Assim, 120 – 30 – 30 = 60 homens torcem pelo Figueirense.
São 80 homens sendo que 30 torcem pelo Avaí e 10 pelo Joinville. Assim, 80 – 30 – 10 = 40 mulheres torcem pelo Figueirense.
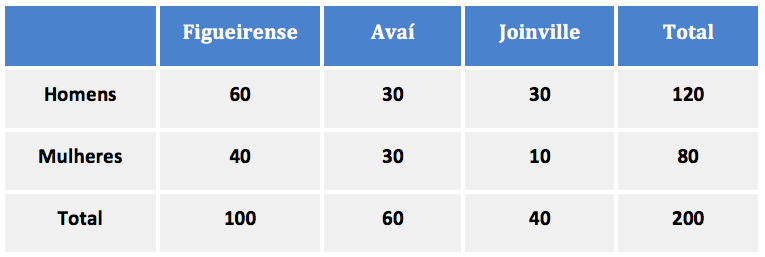
São 200 amigos no total e são 40 mulheres torcedoras do Figueirense. Para calcular a participação percentual dessas mulheres em relação ao total é só dividir 40 por 200 (dividir a parte pelo todo) e multiplicar o resultado por 100%.
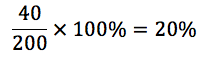
Gabarito: D
Finalmente, chegamos no tópico mais comum nos exercícios de porcentagem, que é a variação percentual.
….
Exemplo nº 01: Imagine a seguinte situação. Você pretende comprar um computador que custa R$ 1.500,00. Como bom “comprador”, pergunta ao vendedor se existe algum tipo de “ajudinha” se você efetuar o pagamento em dinheiro vivo.
O vendedor então informa que, se o pagamento for feito assim, haverá um desconto de R$ 300,00, ou seja, você pagará apenas R$ 1.200,00. Ótimo negócio!!
….
Exemplo nº 02: Imagine agora outra situação. Você pretende comprar um automóvel no valor de R$ 80.000,00. Como bom “comprador”, pergunta ao vendedor se existe algum tipo de “ajudinha” se você efetuar o pagamento em dinheiro vivo.
O vendedor então informa que se o pagamento for feito assim, haverá um desconto de R$ 300,00. Ou seja, você pagará apenas R$ 79.700,00. Foi um ótimo negócio?
….
Em valores absolutos, o desconto do valor do computador foi igual ao desconto do valor do automóvel.
Mas qual dos dois descontos foi mais significativo em relação ao valor inicial do objeto?
Obviamente um desconto de R$ 300,00 em um produto que custa R$ 1.500,00 é bem mais representativo do que um desconto de R$ 300,00 em um produto que custa R$ 80.000,00.
Pois bem, a maneira de comparar esses descontos é a chamada variação percentual.
A razão entre a diferença de valores (valor final menos o valor inicial) e o preço inicial, expressa em forma de porcentagem, é chamada variação percentual.
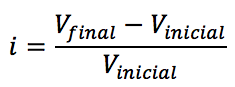
Voltemos aos nossos exemplos:
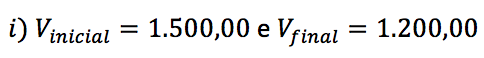
Assim, a taxa percentual é:
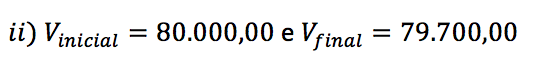
Assim, a taxa percentual é:
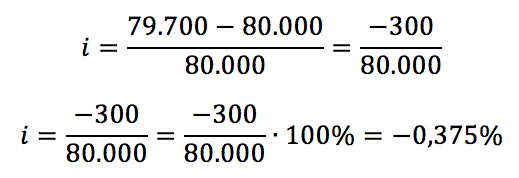
Observe que o desconto no pagamento do computador foi de 20% e o desconto no pagamento do carro foi de apenas 0,375%. Apesar de os valores absolutos dos descontos terem sido iguais, percentualmente a diferença foi gritante.
Para resolver muitos exercícios de porcentagem também é necessário saber calcular variações percentuais sucessivas.
Suponha que uma mercadoria recebeu um desconto de 30%. Se você fosse pagar essa mercadoria sem o desconto, você iria desembolsar 100%. Porém, com o desconto concedido, você irá pagar 100% – 30% = 70%. Assim, para calcular o valor após o desconto, devemos multiplicar o valor original por 70%=70/100.
Em geral, ao diminuir p%, para calcular o valor final, devemos multiplicar por 100% – p%.
Da mesma forma, para aumentar p% de certo valor, devemos multiplicá-lo por 100% + p%.
Por exemplo, se uma mercadoria aumenta 20%, você irá pagar 100% + 20% = 120%.
Exemplo: Uma mercadoria custa R$ 300,00. Em uma primeira ocasião, sofreu um aumento de 40%. Dois meses depois, a loja anunciou uma liquidação e a mercadoria sofreu um desconto de 25%. Qual o valor final da mercadoria? Qual a variação percentual acumulada?
Resolução Quando a mercadoria sofre um aumento de 40%, o cliente além de ter que pagar os 100% (valor da mercadoria) terá que pagar os 40% de aumento. Pagará, portanto, 140% do valor da mercadoria. Dessa forma, a mercadoria, após o aumento, vale:
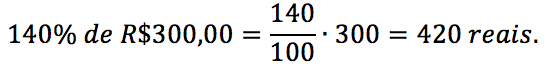
A mercadoria (que agora vale R$ 420,00) sofre um desconto de 25%. Você não pagará o valor total da mercadoria (100%), já que foi concedido um desconto. O cliente pagará 100% – 25% = 75% do valor da mercadoria. Dessa forma, a mercadoria, após o desconto, vale:
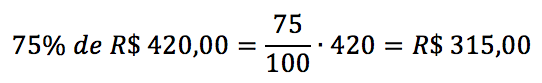
Poderíamos ter efetuado este cálculo de uma maneira mais “objetiva”. Toma-se o valor da mercadoria e multiplica-se pelas taxas de aumentos e de descontos.
Assim,
