Divisão de Polinômios para concursos

Olá, nobres guerreiros. Vamos explanar neste artigo um pouco sobre a divisão de polinômios para concursos. Esse tema é muito cobrado em concursos militares e em cargos específicos como o de professor.

Conceito de polinômios

Por definição, polinômios são expressões matemáticas que possuem números, incógnitas e expoentes inteiros e positivos(normalmente).

Essa definição pode não ter ajudado muito, então vamos a um exemplo: x⁴ – 4x³ + 4x² – 4x +3.

A partir da expressão, ao olharmos o maior expoente do polinômio, no caso acima seria o 4, temos que esse polinômio é de grau 4 e possui 4 soluções(raízes).

Divisão de polinômios

Os polinômios, pessoal, apresentam as mesmas propriedades básicas da matemática, quais sejam: adição, multiplicação, subtração e divisão. Porém, a “queridinha” em concursos é a divisão de polinômios. Assim, as questões de maneira geral apresentarão um polinômio de grau 3 ou superior e te solicitarão as raízes(soluções) ou a divisão deste polinômio por outro.

Para isso, vamos discorrer sobre dois teoremas que vão te ajudar: Teorema de D’Alembert e o dispositivo de Briot-Ruffini.

Teorema de D’Alembert

Por esse teorema, qualquer polinômio dividido por (x-a) que possua resto igual a zero terá “a” como um de suas raízes. Vamos usar nosso exemplo:

Queremos saber se P(X) = x⁴ – 4x³ + 4x² – 4x +3 é divisível por (x – 3). Para isso, onde houver x no polinômio principal, iremos substituir por 3. Logo, temos:

P(3) = 3⁴ – 4 . 3³ + 4 . 3² – 4 . 3+3
P(3) = 81 – 4 . 27 + 4 . 9 – 12 + 3
P(3) = 0

Concluímos, portanto, que 3 é uma das raízes do polinômio acima, vez que P(3)=0

Esse teorema serve para evitar que se proceda à divisão do polinômio por (x – a) de maneira completa. Assim, economiza-se tempo na hora da prova. Então, se ao substituir o “x” no polinômio e sobrar resto zero, temos uma das raízes da equação. Reforçando que o divisor precisa se do tipo (x – a), ok??! Veja como ficaria se fôssemos fazer uma divisão completa:

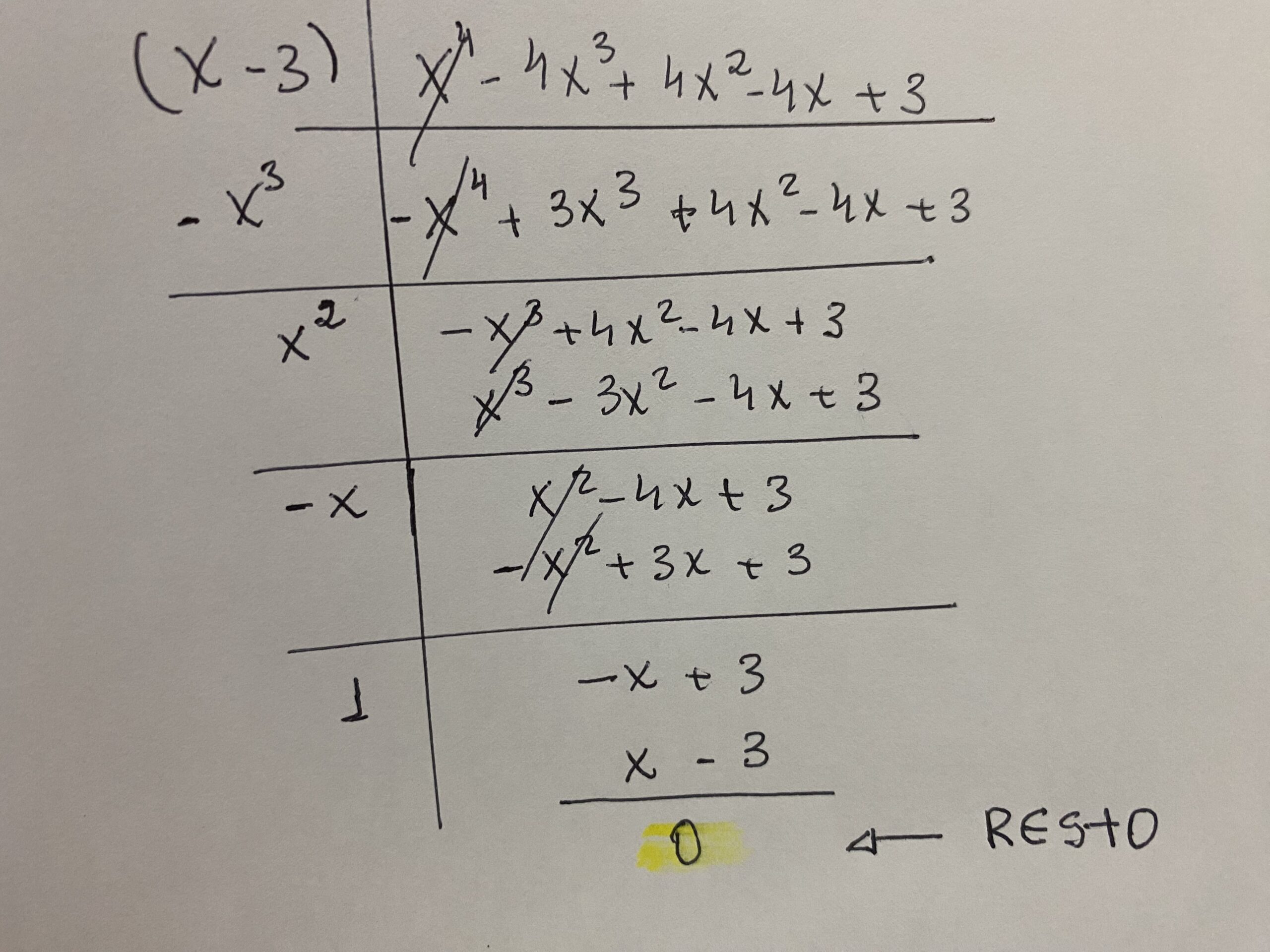
Obs. Multiplica-se cada item do lado esquerdo da imagem por (x – 3) de forma a ir eliminando os coeficientes de maior grau.

Dispositivo de Briot-Ruffini

Pessoal, de maneira prática, usamos o dispositivo de Briot-Ruffini(semelhante à imagem acima) para reduzir o grau de um polinômio e permitir, assim, resolvermos as questões de maneira mais direta(aplicando a fórmula de Bhaskara, por exemplo). Detalharemos melhor a seguir.

Questão com polinômios – Briot-Ruffini

Vamos utilizar o exemplo de uma questão que foi cobrada na prova da Escola Preparatória de Cadetes do Exército aplicada no ano de 2022:

Solução: De início, veja que foi dado que 1 é raiz da equação. Se 1 é raiz, podemos substituir o x por 1 e igualarmos a equação a zero. Fica assim:

P(1) = (M + 39)1 + 1³ – 36 – 14(1²) = 0

M + 39 + 1 – 36 – 14 = 0

M = 10

Com isso, nosso polinômio ficaria assim: X³ – 14X² + 49X – 36

Veja que ainda não conseguimos achar as outras duas raízes devido ao grau da equação ser 3. Contudo, podemos aplicar Briot-Ruffini e reduzirmos o grau do polinômio vez que temos uma raiz já dada no enunciado(1).

Na primeira parte da imagem, detalhamos o local de cada item. Na parte de baixo da imagem, inserimos os valores em que o 1 solitário do lado esquerdo é a raiz dada. Veja que o primeiro coeficiente do polinômio, no caso 1 (1X³) É REPETIDO na parte de baixo(seta azul). A partir daí, multiplica-se cada quociente pela raiz e depois soma-se com o termo correspondente. No caso, 1 x 1 + (-14) = -13. Da mesma forma, -13(1) + 49 = 36, e, por sua vez, 36x(1) – 36 = 0 (resto da operação)

Votando à questão, observem que conseguimos transformar o polinômio de grau 3 em grau 2. Aí, é só aplicar a fórmula de Bhaskara que iremos encontrar 4 e 9 como raízes. Logo, o gabarito da questão é a LETRA C, já que 4 e 9 são quadrados perfeitos.

Questão com polinômios – Teorema de D’Alembert

Por fim, vamos analisar uma questão cobrada no concurso de professor de matemática para a prefeitura de Imperatriz no Maranhão aplicada em 2006 pela FSADU (UFMA):

Ao procurarmos o valor de k, tal que – 2 seja raiz do polinômio P(x)=4X³−2X²+kx−2 obtivemos o seguinte dispositivo de Briot – Ruffini:

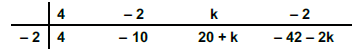
Comentários: Pela imagem que colocamos acima, sabemos que, se -2 é raiz, então (-42 – 2k) precisa valer 0(resto). Logo, (-42 – 2k) = 0, k = -21(gabarito).

Conclusão

Então é isso, nobres. Esperamos que este artigo acerca da divisão de polinômios para concursos seja útil na preparação de vocês. Reforçamos a importância de realizar exercícios para melhor assimilação do conteúdo.

Bons estudos!

Quer estar antenado aos próximos concursos previstos? Confira nossos artigos!

Concursos Abertos

Concursos 2024