Resumo sobre Distribuição Amostral ISS-BH – Estatística
Olá, pessoal. Tudo certo? No artigo de hoje veremos o Resumo sobre Distribuição Amostral ISS-BH.
Os assuntos que serão tratados:
- Distribuição Amostral da Média
- Distribuição Amostral da Proporção
- Distribuição Amostral da Variância
- Estimador Pontual (propriedades e métodos de estimação)
Assim, vamos lá.
Distribuição Amostral
Vamos iniciar o Resumo sobre Distribuição Amostral ISS-BH.
Podemos definir a Distribuição Amostral como a distribuição de probabilidade dos estimadores.
Um ponto muito importante é lembrar que a distribuição de uma amostra aleatória segue a distribuição populacional, em outros termos, a distribuição de probabilidade da amostra é igual à distribuição de probabilidade da população.
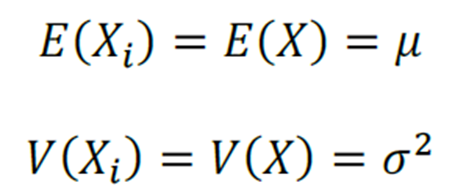
Distribuição Amostral da Média
Dando continuidade ao Resumo sobre Distribuição Amostral ISS-BH, vejamos sobre a Distribuição Amostral da Média.
Vamos conhecer a Esperança da média amostral e a Variância da média amostral.
- Esperança da média amostral
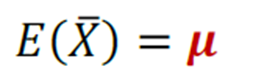
- Variância da média amostral (população infinita)
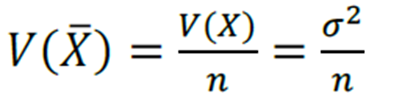
Fator de Correção para População Finita
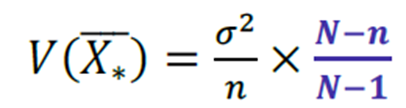
Obs.: Note que diferentemente da esperança da média amostral, a variância da média amostral diminui conforme o tamanho da amostra.
Outra observação a ser feita e que pode gerar alguma confusão é que vimos inicialmente que a variância amostral é igual à variância populacional, entretanto a variância da média amostral é diferente.
Exemplo: (VUNESP/2015 – TJ-SP) Resultados de uma pesquisa declaram que o desvio padrão da média amostral é 32. Sabendo que o desvio padrão populacional é 192, então o tamanho da amostra que foi utilizada no estudo foi
A lógica que vimos para a variância vale para o desvio padrão (lembrando que o desvio padrão é a raiz quadrada da variância), assim:
32 = 192 / raiz n
raiz n = 192/32
raiz n = 6
n = 6²
n = 36
Distribuição Amostral da Proporção
A Distribuição Amostral da Proporção trata-se de uma distribuição em que determinada característica está presente em uma proporção p dessa população.
Assim, caso a proporção populacional seja desconhecida, precisamos estimá-la a partir da proporção de sucessos na amostra.
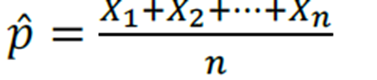
- Esperança do estimador
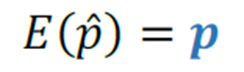
A esperança do estimador é igual à proporção populacional
- Variância do estimador
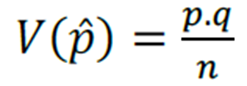
- Estimativa da variância populacional
Como não conhecemos a proporção p, devemos calcular a variância populacional a partir dos estimadores.
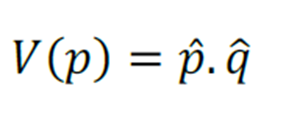
Fator de Correção para População Finita
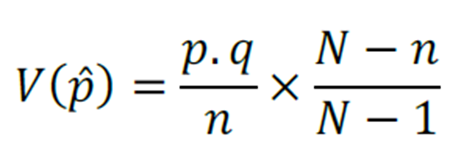
Obs.: Caso de populações pequenas e sem reposição.
Exemplo: (CESPE 2016/TCE-PA) Em estudo acerca da situação do CNPJ das empresas de determinado município, as empresas que estavam com o CNPJ regular foram representadas por 1, ao passo que as com CNPJ irregular foram representadas por 0.
Considerando que a amostra {0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1}
A estimativa pontual da proporção de empresas da amostra com CNPJ regular é superior a 50%.
CORRETO.
Estimador = 12 / 20 -> soma de todos os valores da amostra pelo número de elementos
Estimador = 0,6
Distribuição Amostral da Variância
Da mesma forma que vimos, a Distribuição Amostral da Variância é utilizada quando não conhecemos a variância da população e devemos estimá-la a partir da amostra.
- Estimador da variância
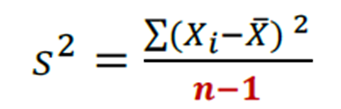
Da mesma forma que para a variância amostral podemos definir que a variância é a diferença entre a média dos quadrados e o quadrado das médias, para o estimador da variância vale o mesmo raciocínio.
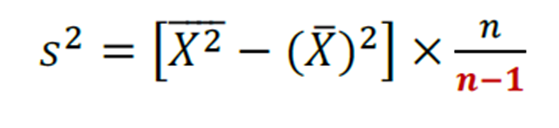
- Esperança, Variância e Desvio Padrão para o estimador s².
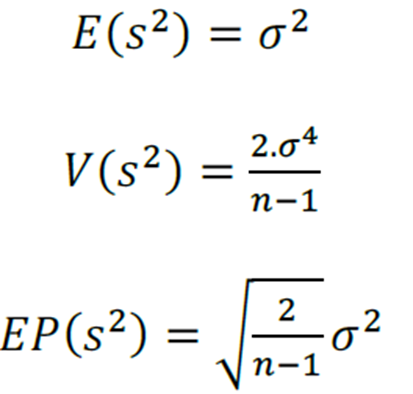
Atente-se que a esperança do estimador é igual à variância populacional.
Estimador Pontual
Prosseguindo no Resumo sobre Distribuição Amostral ISS-BH – Estatística, vamos ver um pouco mais sobre os estimadores.
A estimação pontual nada mais é que o valor calculado pelo estimador.
Inicialmente vimos os estimadores para média amostral, proporção amostral e variância amostral, agora vamos conhecer algumas propriedades.
Propriedades dos Estimadores
Vamos conhecer as Propriedades dos Estimadores.
- Suficiência: A estatística (função dos dados observados) deve ser suficiente, ou seja, contemplar todas informações disponíveis na amostra para estimar o parâmetro populacional.
A distribuição da amostra, condicionada ao parâmetro (ex. média amostral), é independente do parâmetro populacional.
- Não Tendencioso (não viés): A esperança do estimador é igual ao parâmetro populacional
Também podemos entender que a esperança do erro (viés do estimador ou tendenciosidade) deve ser zero para um estimador não tendencioso.
- Eficiente: Dizemos que a variância deve ser a menor possível
Trata-se da variância do erro é igual ao Erro Quadrático Médio (EQM), ou seja, a soma da variância do estimador com o quadrado do viés do estimador.
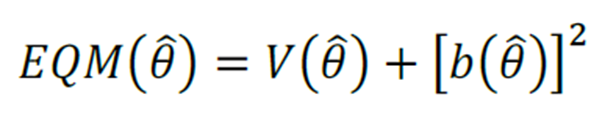
E para estimadores não viesados, o viés do estimador b² é zero.
- Consistente: estimativas convergem com o aumento do tamanho amostral, ou seja, convergem para o parâmetro populacional
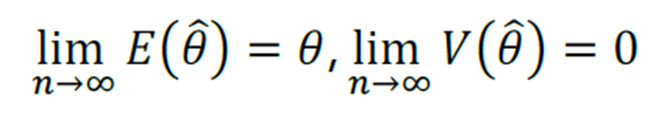
O estimador é consistente se a esperança tende ao estimador e a variância tende a zero, conforme o aumento da amostra.
Métodos de Estimação
Para finalizar o Resumo sobre Distribuição Amostral ISS-BH, vamos ver os Métodos de Estimação.
- Método dos Momentos: baseia-se nos momentos teóricos e amostrais das variáveis aleatórias
Assim, para utilizarmos o método dos momentos (EMM) devemos igualar os momentos teóricos (ou populacionais) aos momentos amostrais.
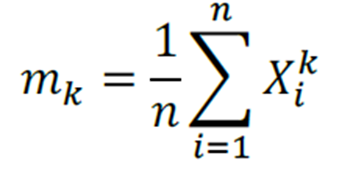
Uma definição interessante dada pela CONSULPLAN: “Este método iguala os momentos da população aos momentos amostrais. Os estimadores são obtidos resolvendo a equação ou o sistema de equações resultante.”
- Método da Máxima Verossimilhança: busca a estimada com maior probabilidade possível entre os valores observados.
Trata-se de um método “complicado”, pois há uma função diferente de acordo com a distribuição da população.
- Método de Mínimos Quadrados: busca a estimativa que resulta no menor valor para o quadrado das diferenças entre os valores observados e o estimador.
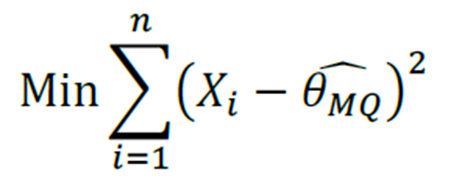
Em outros termos, busca minimizar o erro quadrático total da amostra.
Considerações Finais
Pessoal, chegamos ao final dos Conceitos Iniciais estatística para ISS-BH. Espero que tenham gostado.
Obviamente trata-se de um resumo apenas com os pontos principais da matéria, as aulas são bem aprofundadas em exemplos e explanações além de assuntos que também são importantes como a inferência Bayesiana (ou estatística Bayesiana), assim não deixe de acompanhar as aulas para o aprofundamento necessário.
A estatística, como as matérias de exatas no geral, só se aprende de fato por meio de muito exercícios, logo deixe de praticar.
Sistema de Questões (SQ) – Estratégia Concursos
Gostou do artigo? Não deixe de seguir
https://www.instagram.com/resumospassarin/
Cursos e Assinaturas
Prepare-se com o melhor material e com quem mais aprova em Concursos Públicos em todo o país.
Até mais e bons estudos!