Fala, pessoal!
Tudo bem?
Análise Combinatória é um dos assuntos mais importantes em provas de Matemática e Raciocínio Lógico. É um assunto com poucas fórmulas, mas que causa temor em muitos estudantes pela dificuldade em algumas questões.
Neste artigo vou apresentar um conceito muito legal que certamente te ajudará a ganhar tempo em muitas questões de Análise Combinatória.
Muita atenção neste tópico, pois é uma excelente ferramenta em Análise Combinatória que te ajudará ganhar tempo em muitas questões.
Vamos primeiro entender o que é uma partição de um conjunto. Normalmente, nos problemas de Análise Combinatória, teremos conjuntos de pessoas. Vou explicar então com um conjunto de pessoas para ficar mais fácil.
Imagine que temos um conjunto formado por 7 pessoas. Se queremos dividir esse conjunto de 7 pessoas em subconjuntos disjuntos (que não possuem elemento em comum), obteremos uma partição.
Por exemplo, imagine que queremos dividir esse conjunto de 7 pessoas em 3 subconjuntos: um com 3 pessoas, outro com 2 pessoas e outro com 2 pessoas. Pronto, acabamos de obter uma partição.
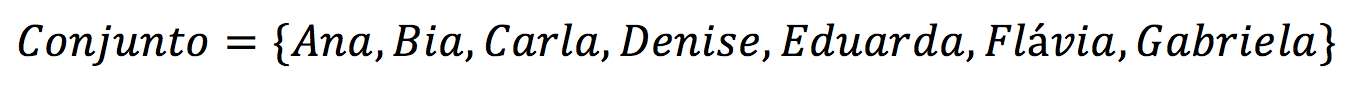
Exemplo de partição:
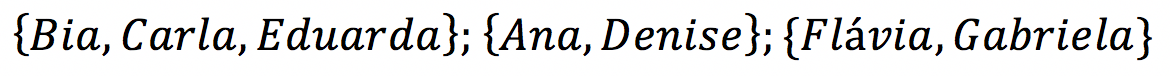
Se a ordem entre esses conjuntos é relevante, a partição é chamada de partição ordenada. Se a ordem não é relevante, a partição é denominada partição não-ordenada.
As partições ordenadas são as mais importantes em questões de concursos. Por quê?
Porque normalmente as pessoas de cada subconjunto terão funções específicas na situação-problema de tal forma que a ordem dos conjuntos será relevante.
Exemplo: Há 7 engenheiros envolvidos em um projeto. Queremos dividir os 7 engenheiros em 2 subconjuntos: 4 deles serão os responsáveis pelo planejamento do projeto e 3 serão responsáveis pela execução do projeto. Temos aqui uma partição ordenada, porque cada subconjunto tem um papel diferente na situação-problema.
Por outro lado, há situações em que a ordem dos conjuntos não é relevante (partições não-ordenadas). Nunca vi essa situação em prova de concurso.
Exemplo: Há 10 crianças que vão jogar futebol. Dividir as crianças em dois times de 5. Aqui temos uma partição não-ordenada, porque a ordem dos times não é relevante.
Observe a seguinte questão:
(CESPE 2019/COGE-CE)
Em determinado órgão, sete servidores foram designados para implantar novo programa de atendimento ao público. Um desses servidores será o coordenador do programa, outro será o subcoordenador, e os demais serão agentes operacionais.
Nessa situação, a quantidade de maneiras distintas de distribuir esses sete servidores nessas funções é igual a
a) 21.
b) 42.
c) 256.
d) 862.
e) 5.040.
O problema acima ilustra perfeitamente a situação de uma partição ordenada. Há 7 pessoas e queremos dividi-las em 3 subconjuntos: um deles com 1 pessoa (o coordenador), outro com 1 pessoa (o subcoordenador) e outro com 5 pessoas (os agentes operacionais).
Normalmente, os livros resolvem esse tipo de problema assim:
Há 7 pessoas disponíveis e precisamos escolher 1 coordenador. Podemos escolher de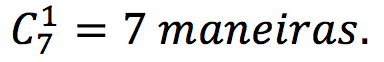 
Sobraram 6 pessoas disponíveis. Devemos agora escolher 1 subcoordenador. Podemos escolher de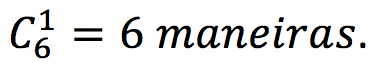 
Sobraram 5 pessoas. Devemos escolher 5 agentes operacionais. Podemos escolher de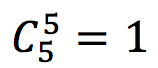 
maneira.
Como há ordem entre os subconjuntos (1 deles é o coordenador, o outro é o subcoordenador, e os restantes são agentes operacionais), a partição é ordenada. Não estou dizendo que existe ordem entre os elementos dos subconjuntos. Existe ordem entre os subconjuntos!
Pelo princípio fundamental da contagem, o total de possibilidades é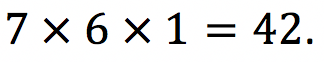 
Poderíamos também ter começado escolhendo os agentes operacionais.
Há 7 pessoas disponíveis e precisamos escolher 5 agentes operacionais. Podemos escolher de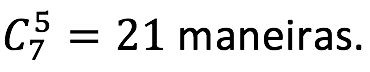 
Sobraram 2 pessoas. Dessas duas pessoas, precisamos escolher 1 coordenador. Podemos escolher de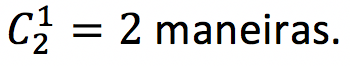 
Sobrou 1 pessoa. Precisamos escolher o subcoordenador. Podemos escolher de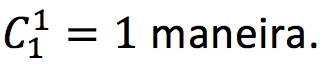 
Pelo princípio fundamental da contagem, podemos distribuir os servidores nas funções de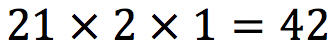 
maneiras.
Vamos agora aprender o pulo do gato: a grande dica que te fará ganhar muito tempo nessas questões.
Há 7 pessoas e queremos dividi-las em 3 subconjuntos com 1 pessoa (o coordenador), 1 pessoa (o subcoordenador) e 5 pessoas (os agentes operacionais). Vamos simbolizar essa quantidade de partições da seguinte forma:
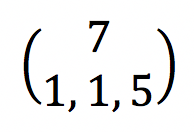
A expressão acima é conhecida como “coeficiente multinomial”.
Pois bem, como calculamos? É muito fácil. A resposta será uma fração. No numerador, colocamos o fatorial de 7, que é o fatorial do conjunto original de pessoas. No denominador, colocamos os fatoriais das quantidades de elementos dos subconjuntos (fatoriais de 1, 1, e 5).
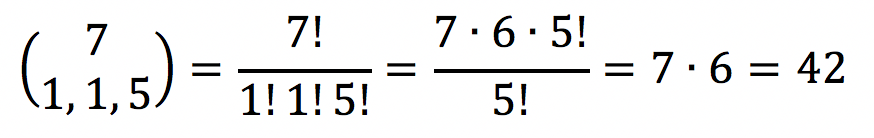
Muito fácil, não?
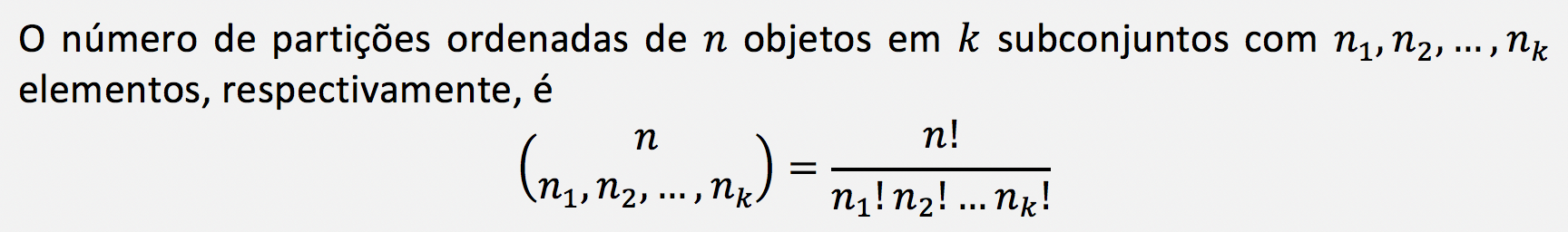
Vamos resolver outros exemplos para por em prática e para que você perceba o poder desse método.
(CESPE 2014/PMCE)
Considerando que um grupamento de 60 policiais militares em que haja 15 mulheres e 45 homens seja dividido em 10 equipes de 6 militares para monitorar determinada área, julgue o item subsequente.
Se as 2 primeiras equipes formadas forem constituídas apenas por mulheres, então o número de maneiras distintas de escolher os membros dessas equipes será igual a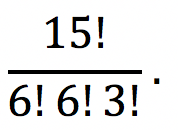 
Resolução
Vamos primeiro resolver da forma “tradicional” utilizando combinações.
Há 15 mulheres e devemos escolher 6 para a primeira equipe. Em seguida, sobram 9 mulheres das quais devemos escolher 6 para a segunda equipe.
Observe que queremos colocar 6 mulheres na primeira equipe e 6 mulheres na segunda equipe. Como o conectivo usado é “e”, devemos multiplicar as quantidades.
O total de maneiras para escolher os membros dessa equipe é
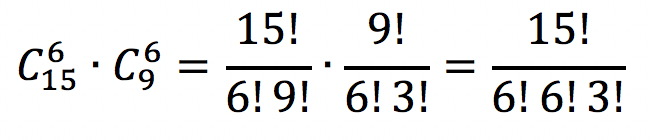
Vamos agora utilizar partições.
Há 15 mulheres e vamos dividir em dois grupos de 6 mulheres. Observe que sobraram 3 mulheres. Essas 3 mulheres formam um terceiro subconjunto. Assim, na verdade, estamos dividindo as 15 mulheres em 3 subconjuntos: dois subconjuntos com 6 mulheres e um terceiro com 3 mulheres.
Sempre que sobrarem pessoas, você deve juntar a “sobra” em um último subconjunto.
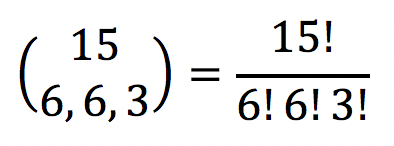
Gabarito: Certo.
(CESPE 2018/PM-MA)
Uma operação policial será realizada com uma equipe de seis agentes, que têm prenomes distintos, entre eles André, Bruno e Caio. Um agente será o coordenador da operação e outro, o assistente deste; ambos ficarão na base móvel de operações nas proximidades do local de realização da operação. Nessa operação, um agente se infiltrará, disfarçado, entre os suspeitos, em reunião por estes marcada em uma casa noturna, e outros três agentes, também disfarçados, entrarão na casa noturna para prestar apoio ao infiltrado, caso seja necessário.
A respeito dessa situação hipotética, julgue o item seguinte.
Há mais de 100 maneiras distintas de estruturar, com os seis agentes, a equipe que realizará a operação policial.
Resolução
Há 6 agentes disponíveis. Um será o coordenador, o outro o assistente, o outro o infiltrado, e os outros 3 serão agentes disfarçados.
Assim, precisamos dividir o conjunto de 6 agentes em 4 subconjuntos com as seguintes quantidades de elementos: 1, 1, 1 e 3. Como cada conjunto tem um papel distinto no problema (um é coordenador, o outro é o assistente, e assim por diante), então vamos calcular o total de partições ordenadas.
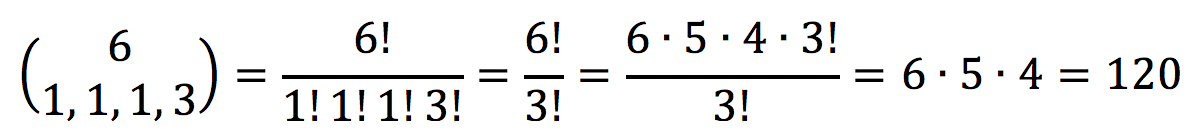
Gabarito: Certo
(CESPE 2015/MPOG)
Determinado órgão público é composto por uma diretoria geral e quatro secretarias; cada secretaria é formada por três diretorias; cada diretoria tem quatro coordenações; cada coordenação é constituída por cinco divisões, com um chefe e sete funcionários subalternos em cada divisão.
A respeito desse órgão público, julgue os itens seguintes, sabendo que cada executivo e cada funcionário subalterno só pode ocupar um cargo nesse órgão.
Se, entre onze servidores previamente selecionados, forem escolhidos: sete para compor determinada divisão, um para chefiar essa divisão, um para a chefia da coordenação correspondente, um para a diretoria e um para a secretaria, haverá menos de 8.000 maneiras distintas de se fazer essas escolhas.
Resolução
Há 11 servidores e vamos dividi-los em subconjuntos (partições). Cada subconjunto tem uma função específica. Logo, queremos calcular a quantidade de partições ordenadas.
Os subconjuntos terão as seguintes quantidades de elementos: 7, 1, 1, 1, 1. Logo, o número de partições ordenadas é
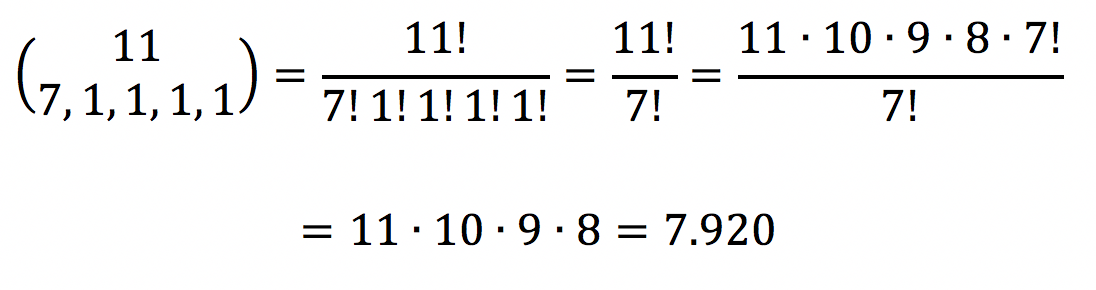
Gabarito: Certo
(CESPE 2013/IBAMA)
Para melhorar a fiscalização, evitar o desmatamento ilegal e outros crimes contra o meio ambiente, 35 fiscais homens e 15 fiscais mulheres serão enviados para a região Norte do Brasil. Desses fiscais, uma equipe com 20 fiscais será enviada para o Pará, outra com 15 para o Amazonas e uma outra com 15 para Rondônia.
Considerando que qualquer um desses 50 fiscais pode ser designado para qualquer uma das três equipes, julgue os itens seguintes.
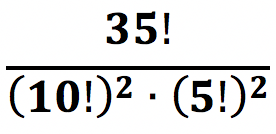.Resolução
Item 1
Há 50 fiscais. Vamos dividi-los em 3 subconjuntos com as seguintes quantidades de elementos: 20, 15 e 15. O total de partições ordenadas é
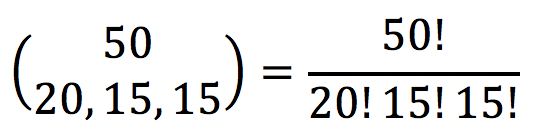
O item 1 está errado.
Item 2
Há 15 mulheres e vamos dividi-las em três grupos de 5.
Há 35 homens e vamos dividi-los em três grupos: um dos grupos terá 15 (Pará), o outro grupo terá 10 (Amazonas) e o outro terá 10 (Rondônia).
O total de partições ordenadas será:
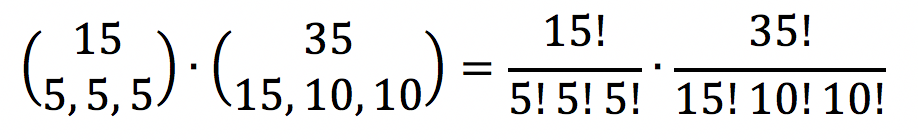
Podemos cortar 15!. Além disso, perceba que:
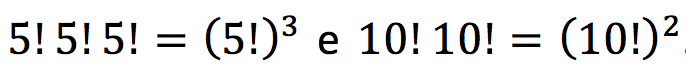
Logo, a resposta do problema é:
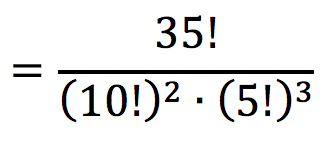
O item trocou o expoente de 5! por 2. Logo, o item 2 está errado.
Espero que tenham gostado das dicas sobre partições ordenadas.
Um forte abraço,
Guilherme Neves