Como estudar Matemática e Raciocínio Lógico para PCDF?
Alguns alunos têm muita facilidade com Matemática e Raciocínio Lógico e as adoram, enquanto outros acreditam que elas poderão ser a causa principal de uma reprovação no concurso. Mostraremos, principalmente a esse segundo grupo, como estudar Matemática e Raciocínio Lógico para PCDF e que, com algum estudo, é possível obter um bom desempenho nessas matérias.
Lembrando que já temos um artigo similar (Como estudar Matemática e RLM para a PC-DF em 90 dias?), mas que possui o foco na análise mais aprofundada, aula a aula. Por outro lado, este nosso artigo busca trazer outra abordagem, com alguns exemplos de questões por tópico.
Os estudos e a hora da prova
Como em qualquer disciplina, você deve antes de tudo ler o edital e verificar quais tópicos você domina e quais você não conhece ou não domina. Você deve inicialmente dar mais atenção aos conteúdos que considera mais difíceis para ter mais tempo para assimilá-los.
Isso muda na hora da prova. Tanto em relação às disciplinas quanto em relação ao conteúdo de cada disciplina, faça primeiro as questões que achar mais fáceis. Isso te trará confiança. Você ficará menos nervoso se não souber a resposta de uma questão após ter respondido 8 questões do que se não tiver respondido nenhuma.
Ah, e até para os candidatos com facilidade em Matemática e RLM: começar a prova por essa matéria pode te custar alguns pontos. No início da prova, os candidatos costumam estar mais desatentos e ainda não se acostumaram com o ambiente. Não deixe o nervosismo atrapalhar seus cálculos e te fazer escorregar nas cascas de banana: pense em começar a prova por outra disciplina. Fica aí a importância de saber como estudar Matemática e Raciocínio Lógico para PCDF.
Conhecimentos exigidos no edital
| 1 Princípios de contagem. | 9 Estruturas lógicas. |
| 2 Razões e proporções. | 10 Lógica de argumentação. |
| 3 Regras de três simples. | 11 Lógica sentencial (ou proposicional). |
| 4 Porcentagens. | 12 Lógica de primeira ordem. |
| 5 Equações de 1º e de 2º graus. | 13 Princípios de contagem e probabilidade. |
| 6 Sequências numéricas. | 14 Operações com conjuntos. |
| 7 Progressões aritméticas e geométricas. | 15 Raciocínio lógico envolvendo problemas aritméticos, geométricos e matriciais. |
| 8 Funções e gráficos. |
Faremos alguns exercícios para verificar como são cobrados cada tópico. O intuito deste artigo não é fornecer resoluções de cada uma das questões ou fornecer informações exaustivas sobre o edital, mas apenas mostrar linhas gerais do que é esperado que o candidato saiba em cada assunto, facilitando e indicando como estudar Matemática e Raciocínio Lógico para PCDF.
1 Princípios de contagem
Escrivão de Polícia Federal – CESPE – 2018
Para cumprimento de um mandado de busca e apreensão serão designados um delegado, 3 agentes (para a segurança da equipe na operação) e um escrivão. O efetivo do órgão que fará a operação conta com 4 delegados, entre eles o delegado Fonseca; 12 agentes, entre eles o agente Paulo; e 6 escrivães, entre eles o escrivão Estêvão.
Há mais de 2.000 maneiras distintas de se formar uma equipe que tenha o delegado Fonseca ou o escrivão Estêvão, mas não ambos.
RESOLUÇÃO: Em questões de contagem, temos primeiro que verificar se a ordem importa (permutação) ou se não importa (combinação). Neste exercício, a ordem não importa na escolha do funcionário dentre seus pares.
Calcularemos primeiro o número de equipes com o delegado Fonseca e sem o escrivão Estevão:
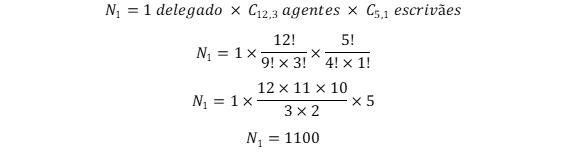
Então, calcularemos o número de equipes com o escrivão Estevão e sem o delegado Fonseca:

Assim, o número total de equipes que atendem ao enunciado é de 1100 + 660 = 1760 < 2000. Isso significa que o enunciado está ERRADO!
2 Razões e Proporções
Analista Judiciário do STM – Contabilidade – CESPE – 2018
Os irmãos Jonas, Pierre e Saulo, que têm, respectivamente, 30, 20 e 18 anos de idade, herdaram de seu pai a quantia de R$ 5 milhões. O testamento prevê que essa quantia deverá ser dividida entre os irmãos em partes inversamente proporcionais às suas idades.
Nessa situação hipotética, Jonas receberá 50% a mais que Saulo.
RESOLUÇÃO: Em questões desse tipo, o mais difícil é montar corretamente a equação com as grandezas. No caso do enunciado, a herança será dividida de forma inversamente proporcional às idades, ou seja, o irmão mais velho ganhará menos.
Nem precisamos calcular nada para ver que o enunciado está ERRADO, pois Jonas é o irmão mais velho, e por isso deve receber menos. Muitas vezes a CESPE coloca questões que não precisam de cálculo para ajudar o candidato atento (ou atrasar o desatento).
O cálculo que deveria ser feito caso o enunciado não fosse evidentemente incorreto seria:
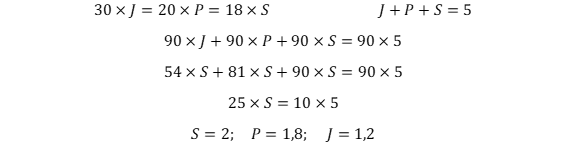
3 Regras de três simples
Analista Administrativo de PGE-PE – Calculista – CESPE – 2019
No primeiro dia de abril, o casal Marcos e Paula comprou alimentos em quantidades suficientes para que eles e seus dois filhos consumissem durante os 30 dias do mês. No dia 7 desse mês, um casal de amigos chegou de surpresa para passar o restante do mês com a família. Nessa situação, se cada uma dessas seis pessoas consumir diariamente a mesma quantidade de alimentos, os alimentos comprados pelo casal acabarão antes do dia 20 do mesmo mês.
RESOLUÇÃO: Quando o enunciado te informa uma situação e pede para, a partir dela, verificar outra situação, nos deparamos com a regra de três. No edital, está prevista apenas a regra de três simples, que, como o próprio nome diz, é mais simples de entender do que a composta, facilitando o raciocínio e os estudos.
O casal comprou comida para 4 pessoas consumirem por 30 dias. No 7º dia, quando ainda restavam 24 dias de planejamento de consumo, um casal de amigos chega e começa a comer da mesma comida. Temos que verificar até quando os alimentos comprados durarão.
O número de dias que a comida durará é inversamente proporcional ao número de pessoas presentes. Quanto mais pessoas, menos a comida durará. Assim:
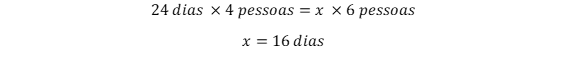
Como a chegada do novo casal só ocorre no 7º dia, haverá alimentos até o dia 22. Por isso, o enunciado está ERRADO.
4 Porcentagens.
Analista Administrativo de PGE-PE – Calculista – CESPE – 2019
O casal Rafael e Joana investe R$ 2.000 todos os meses. Joana investe 50% a mais que Rafael e o valor investido por cada um corresponde a 25% dos seus respectivos salários líquidos. Nessa situação, o salário líquido de Rafael é de R$ 3.200.
RESOLUÇÃO: Algumas questões do CESPE costumam atordoar o candidato com excesso de informações. É preciso parar um pouco e analisar o enunciado por partes:
O casal Rafael e Joana investe R$ 2.000 todos os meses:
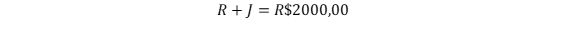
Joana investe 50% a mais que Rafael:
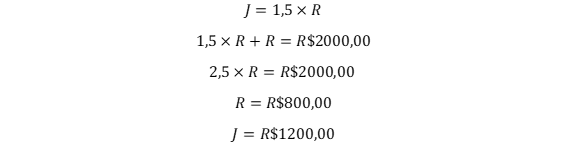
O valor investido por cada um corresponde a 25% dos seus salários:
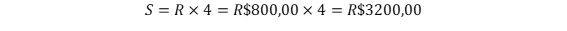
Dessa forma, vemos que o enunciado está CORRETO.
5 Equações de 1º e de 2º graus.
Agente Administrativo do MDIC – CESPS – 2014
Caso a quantidade diária de camisetas produzidas por uma indústria entre x -1 e x horas do dia seja expressa por f(x) = – 4x² + 100x – 400, em que 7 ≤ x ≤ 18, então a quantidade máxima de camisetas produzida por essa indústria ocorrerá entre 13 e 14 horas.
RESOLUÇÃO: Em funções de 2º grau, existem alguns macetes que ajudam a resolver o exercício mais rapidamente. Quando queremos o ponto máximo ou mínimo de uma função, o método mais prático é derivá-la e igualar a 0. Porém, para quem não sabe fazer isso, basta encontrar os zeros da função. O ponto máximo (ou mínimo) é o ponto médio entre eles. Assim:
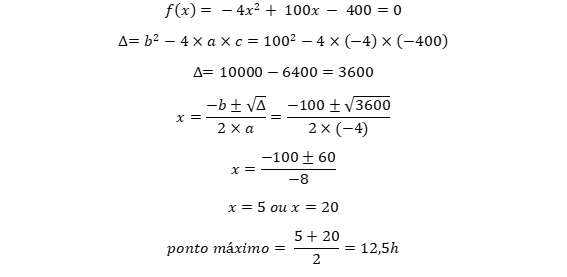
Assim, o enunciado está ERRADO, pois o ponto máximo ocorre às 12h30min.
6 Sequências numéricas.
Especialista Técnico do BNB – Analista de Sistema – CESPE – 2018
A sequência infinita A1, A2, A3, A4, … é definida da seguinte maneira: para cada j = 1, 2, 3, 4, …,
Aj = 1, se j for múltiplo de 3;
Aj = 3, se j – 1 for múltiplo de 3;
Aj = 5, se j – 2 for múltiplo de 3.
Dessa forma, por exemplo, A1 = 3 e A2 = 5. Com base nessas informações, a soma dos primeiros 60 termos dessa sequência é igual a 160.
RESOLUÇÃO: Em questões de sequência numérica, cuidado para não perder muito tempo tentando descobrir a fórmula da sequência. Por mais óbvia que ela seja, você pode não conseguir visualizá-la mesmo que invista todo o tempo de prova na questão. Deixe a questão pro fim caso você trave nela.
No caso do enunciado, a fórmula já foi dada. Isso facilita muito a resolução. Os dois primeiros números da sequência foram dados. Os seguintes, deduzimos pela fórmula:
| j | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Aj | 3 | 5 | 1 | 3 | 5 | 1 | 3 | 5 | 1 | 3 | 5 | 1 | 3 | 5 |
Não precisamos ir muito longe para verificar que a sequência se repete a cada 3 números. Como 60 = 3 x 20, a sequência se repetirá 20 vezes nos 60 primeiros termos.
A soma dos 3 números que se repetem é igual a 3 + 5 + 1 = 9. Assim, a soma dos 60 primeiros termos é igual a 20 x 9 = 180. Assim, o enunciado está ERRADO.
7 Progressões aritméticas e geométricas.
Agente de Polícia Legislativa da Câmara dos Deputados – CESPE – 2014
Em determinado colégio, todos os 215 alunos estiveram presentes no primeiro dia de aula; no segundo dia letivo, 2 alunos faltaram; no terceiro dia, 4 alunos faltaram; no quarto dia, 6 alunos faltaram, e assim sucessivamente.
No vigésimo quinto dia de aula, faltaram 50 alunos.
RESOLUÇÃO: Em questões de PA ou PG, lembrar-se das fórmulas ajuda a encontrar a resposta mais rápido. De qualquer forma, resolver o exercício na força bruta sempre pode ser uma opção quando são “poucos” os termos na progressão, até para confirmar se você não errou fórmulas ou contas.
Cuidado também para não cair em pegadinhas. O CESPE costuma fazer questões que parecem muito fáceis apenas para você sentir confiança e errar com convicção.
Nessa questão, temos uma PA de razão 2 e termo inicial igual a 215. Assim:
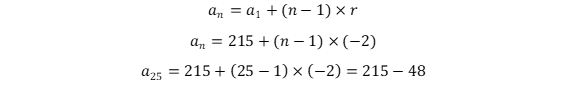
Nesse ponto do cálculo, já concluímos que faltaram 48 alunos, o que torna o enunciado ERRADO.
O candidato apressado calculará que faltaram 25 dias x 2 alunos/dia = 50 alunos, esquecendo-se de descontar o primeiro dia da conta. Não seja esse candidato.
8 Funções e gráficos.
Policial Rodoviário Federal – CESPE – 2002
Mortes por atropelamento sobem no período de redução da iluminação
As mortes por atropelamento dispararam em municípios que reduziram a iluminação das ruas no racionamento de energia elétrica, encerrado anteontem. Os dados mostram uma inversão na tendência de queda das mortes desde a implantação do CTB, em 1998, exceto em municípios que criaram alternativas para minimizar a falta de iluminação e na região Sul do país.
Os dados disponíveis comprovam aquilo que os especialistas previam, já que mais da metade dos atropelamentos ocorrem à noite. Mas as medidas atenuantes, em geral, não foram tomadas. O racionamento foi instituído em 21/5/2001. A partir dessa data, as prefeituras tiveram um prazo até 30 de junho para reduzir em 35% a carga de energia da iluminação pública.
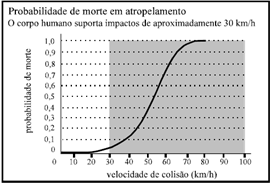
É impossível encontrar números reais a, b e c tais que o gráfico da função f(x) = ax2 + bx + c coincida com o gráfico ilustrado na figura, em que x é a velocidade de colisão e f(x) é a probabilidade de morte.
RESOLUÇÃO: Exercícios de gráficos costumam apenas exigir que o candidato saiba analisá-lo e conheça as formas das principais funções. Sabemos que a função polinomial de segunda ordem (x²) tem a forma de um U (para cima ou para baixo), atingindo um ponto mínimo ou máximo e tendendo a infinito nos extremos.
Não gaste tempo tentando confundir sua cabeça para ver se há números reais que consigam representar a função dada no gráfico. Ele não tem a forma de U e não tende a infinito em nenhum dos lados. O enunciado está ERRADO.
9 a 12 Estruturas lógicas, Lógica de argumentação, Lógica sentencial (ou proposicional), Lógica de primeira ordem.
Os assuntos desses tópicos do edital foram agrupados porque dizem respeito ao mesmo conteúdo: proposições lógicas. Por isso, os trabalharemos em conjunto, apresentando três questões sobre eles.
Entretanto, não desconsidere sua importância: o CESPE adora cobrar proposições lógicas e costuma basear várias questões num mesmo enunciado.
Agente de Polícia Federal – CESPE – 2018
As proposições P, Q e R a seguir referem-se a um ilícito penal envolvendo João, Carlos, Paulo e Maria:
P: “João e Carlos não são culpados”.
Q: “Paulo não é mentiroso”.
R: “Maria é inocente”.
Considerando que ~X representa a negação da proposição X, julgue os itens a seguir.
As proposições P, Q e R são proposições simples.
RESOLUÇÃO: As proposições Q e R são claramente simples. Cada uma apresenta apenas uma afirmativa que pode ser considerada verdadeira ou falsa.
A proposição P, por outro lado, pode ser analisada de duas maneiras diferentes. Se considerarmos o sujeito composto “João e Carlos”, P será uma proposição simples. Por outro lado, se considerarmos que P é equivalente a “João não é culpado e Carlos não é culpado”, a proposição será considerada composta.
Historicamente, o posicionamento do CESPE era de que, quando havia um só verbo, a proposição deveria ser considerada simples. Porém, nessa prova, ela anulou a questão com a justificativa de que “há divergência de literatura a respeito do tipo de proposição disposto no item”.
Estudar por um material completo, atualizado e direcionado para o edital, vai te ajudar a saber como responder o que a banca considera correto e não perder pontos por descuido.
Se ficar comprovado que apenas um dos quatro envolvidos no ilícito penal é culpado, então a proposição simbolizada por (~P)→(~Q)∨R será verdadeira.
RESOLUÇÃO: Temos que destrinchar o enunciado para identificar como analisá-lo de uma forma mais simples. Ele trabalha com a hipótese de apenas um dos quatro envolvidos ser culpa.
A proposição P afirma que dois deles não são culpados, ou seja, ~P = João e Paulo são culpados. Assim, ela bate de frente com o proposto no enunciado, e por isso é falsa.
A tabela verdade da proposição com se é dada por:
| P | Q | P → Q |
| V | V | V |
| V | F | F |
| F | V | V |
| F | F | V |
Se o antecedente é falso, a proposição será verdadeira não importando o valor do consequente. Assim, a afirmação proposta no enunciado está CORRETA.
Se as três proposições P, Q e R forem falsas, então pelo menos duas das pessoas envolvidas no ilícito penal serão culpadas.
RESOLUÇÃO: Temos que negar as três proposições para ver o resultado:
~P: “João e Carlos são culpados”. → 2 culpados
~Q: “Paulo não é mentiroso”. → ?
~R: “Maria não é inocente”. → 1 culpado
Assim, vemos que, caso as três proposições sejam falsas, temos 3 ou 4 culpados (não podemos afirmar nada sobre Paulo). Isso significa que há pelo menos dois culpados e o enunciado está CORRETO.
13 Princípios de contagem e probabilidade.
Esse tópico deve ser estudado em conjunto com o tópico 1. Não diferem muito entre si. A parte de probabilidade também pode vir associada ao tópico seguinte (operações com conjuntos, quando temos que calcular a probabilidade da interseção ou condicional. Faremos aqui dois exercícios abordando probabilidade e combinação.
Inspetor de Controle Externo do TCE-RN – CESPE – 2015
Para fiscalizar determinada entidade, um órgão de controle escolherá 12 de seus servidores: 5 da secretaria de controle interno, 3 da secretaria de prevenção da corrupção, 3 da corregedoria e 1 da ouvidoria. Os 12 servidores serão distribuídos, por sorteio, nas equipes A, B e C; e cada equipe será composta por 4 servidores. A equipe A será a primeira a ser formada, depois a equipe B e, por último, a C.
A probabilidade de um servidor que não for sorteado para integrar a equipe A ser sorteado para integrar a equipe B é igual a 0,5.
RESOLUÇÃO: Quando todos os membros da equipe A são sorteados, restam 12 – 4=8 servidores. A equipe B também será formada por 4 servidores. Se pensarmos em um servidor específico, precisamos encontrar quantas combinações da equipe B o incluirão para determinar a probabilidade de ele ficar nessa equipe.
O total de combinações possíveis para a equipe B é dado por:
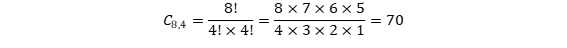
O número de combinações não incluindo um servidor específico não sorteado para integrar a equipe A é dado por:
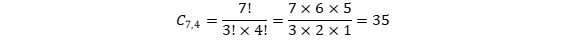
Assim, a probabilidade de um servidor não sorteado para integrar a equipe A ser sorteado para integrar a equipe B é dada por:
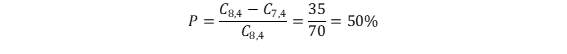
Também podemos pensar que, se o servidor não está na equipe A e as equipes são formadas pelo mesmo número de servidores, a probabilidade de ele estar em cada uma é a mesma (50%). Assim, o enunciado está CORRETO.
A chance de a equipe A ser composta por um servidor de cada unidade é superior a 10%.
RESOLUÇÃO: Combinações possíveis para a equipe A:
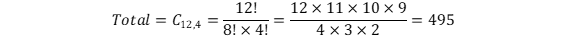
Combinações com uma pessoa de cada equipe:
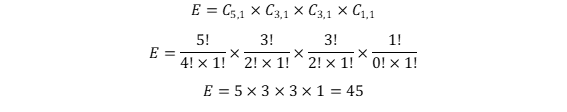
Probabilidade de haver um servidor de cada unidade na equipe A:
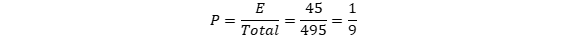
Como sabemos que 1/9 é maior que 1/10, sabemos sem fazer contas que P>10%. Assim, o enunciado está CORRETO.
14 Operações com conjuntos.
Agente de Polícia Federal – CESPE – 2018
Em um aeroporto, 30 passageiros que desembarcaram de determinado voo e que estiveram nos países A, B ou C, nos quais ocorre uma epidemia infecciosa, foram selecionados para ser examinados. Constatou-se que exatamente 25 dos passageiros selecionados estiveram em A ou em B, nenhum desses 25 passageiros esteve em C e 6 desses 25 passageiros estiveram em A e em B.
Se 11 passageiros estiveram em B, então mais de 15 estiveram em A.
RESOLUÇÃO: Existem várias formas de se resolver esse exercício. A mais visual e intuitiva é o Diagrama de Venn. Preenchemos ele com as informações que possuímos:
– 25 passageiros não estiveram em C → 5 passageiros estiveram em C.
– Nenhum passageiro que esteve em A ou B esteve em C → interseção nula entre C e outros.
– 6 passageiros estiveram em A e B. Assim:
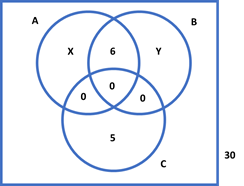
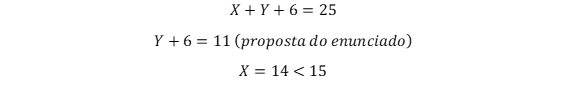
Assim, vemos que o enunciado está ERRADO.
Considere que, separando-se o grupo de passageiros selecionados que visitou o país A, o grupo que visitou o país B e o grupo que visitou o país C, seja verificado, em cada um desses grupos, que pelo menos a metade dos seus componentes era do sexo masculino. Nessa situação, conclui-se que o grupo de 30 passageiros selecionados tem, no máximo, 14 mulheres.
RESOLUÇÃO: O enunciado afirma que pelo menos a metade dos passageiros de cada grupo são homens. No grupo C, para que isso ocorra, deve haver pelo menos 3 passageiros homens. Já nos grupos A e B, temos que, se há mais homens em cada um dos grupos, isso também ocorre na soma deles. Assim:
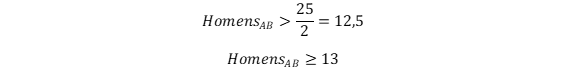
Isso significa que há, no mínimo, 13 + 3 = 16 homens entre os 30 passageiros, ou seja, há no máximo 14 mulheres. Por isso, o enunciado está correto.
15 Raciocínio logico envolvendo problemas aritméticos, geométricos e matriciais.
Tópico existente para que a banca possa cobrar qualquer assunto envolvendo raciocínio lógico sem correr o risco de fugir ao edital. Faremos um exercício de raciocínio envolvendo problema aritmético.
Técnico em Gestão de Telecomunicações da Telebras – CESPE – 2015
A equipe de atendentes de um serviço de telemarketing é constituída por 30 empregados, divididos em 3 grupos, que trabalham de acordo com a seguinte escala.
Grupo I: 7 homens e 3 mulheres, que trabalham das 6 h às 12 h.
Grupo II: 4 homens e 6 mulheres, que trabalham das 9 h às 15 h.
Grupo III: 1 homem e 9 mulheres, que trabalham das 12 h às 18 h.
Se, entre os atendentes do sexo masculino, o mais velho tiver nascido em 1982 e o mais novo, em 1986, então pelo menos 3 dos atendentes do sexo masculino nasceram em um mesmo ano.
RESOLUÇÃO: São 12 atendentes homens. Sabendo que o mais velho nasceu em 1982 e o mais novo, em 1986, temos 5 anos possíveis para o nascimento de cada um. Para saber se pelo menos 3 atendentes nasceram em um mesmo ano, temos que verificar se é possível que no máximo 2 atendentes tenham nascido no mesmo ano.
Distribuindo uniformemente os atendentes pelos anos, temos:
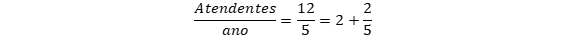
Isso significa que não é possível que existam no máximo 2 atendentes nascidos no mesmo ano (sobram 2), ou seja, pelo menos 3 dos atendentes do sexo masculino nasceram em um mesmo ano. Dessa forma, o enunciado está CORRETO.
Conclusão
O edital de Matemática e Raciocínio Lógico para o concurso da PCDF está bem tranquilo, não é mesmo? Lembre-se que se a prova vier muito difícil, ela virá assim para todos. O importante é estar preparado, e, para isso, tenha um bom material ao seu lado e faça muitos exercícios.
E aí? Aprendeu como estudar Matemática e Raciocínio Lógico para PCDF?
Saiba mais informações: Concurso PCDF
Quer estudar para Concurso PCDF?
Gostou desta oportunidade e deseja começar se preparar agora mesmo? Então, confira os nossos cursos e comece a estudar para o concurso PC DF:
Assinatura Anual Ilimitada*
Prepare-se com o melhor material e com quem mais aprova em Concursos Públicos em todo o país. Assine agora a nossa Assinatura Anual e tenha acesso ilimitado* a todos os nossos cursos.
ASSINE AGORA – Assinatura Ilimitada