Olá, queridas e queridos! Tudo bem? O foco desse artigo será desvendar os mistérios de como estudar Estatística para concursos. Faremos também uma análise contextual da matéria: em quais concursos é cobrada, quais são os principais temas e maiores dificuldades. Vamos lá!
Estamos falando de uma disciplina cobrada em diversas áreas de concursos. Nos últimos anos, sua cobrança, nas provas da área Fiscal e de Controle, tem aumentado bastante. Além disso, concursos renomados, como Banco Central, também incluem a disciplina no edital, sem contar os diversos concursos para profissionais formados em Estatística.
Trata-se de uma disciplina bastante temida pelos candidatos. Muitas vezes, mesmo com sua presença no edital, alunos tomam a decisão de não a estudar. Sabemos que isso traz consequências perigosas devido ao nível de competição dos concursos nos dias de hoje.
Muitos avaliam seu custo benefício como baixo, porém, estudando seu conteúdo com estratégia, ela pode resultar em valiosos pontos. Assim, percebemos o real valor de possuir técnicas apuradas sobre como estudar Estatística.
Para ficar craque em como estudar Estatística é necessário conhecer seus principais temas. Aqueles mais cobrados em concursos são:
Probabilidade, em alguns casos, é um assunto incluído em Raciocínio Lógico Matemático e que faz parte do currículo do ensino médio brasileiro. A ideia é calcular a probabilidade de um certo evento acontecer, levando em consideração variáveis da situação.
Trata-se, dentro dos tópicos citados, daquele que possui o maior número de variações de exercícios possível. A teoria é enxuta, sem muitas fórmulas ou conceitos, mas, por outro lado, resulta em infinitas possibilidades distintas de cobrança. Dessa forma, é necessário que o candidato realize extensas baterias de questões para tentar se familiarizar com a maior quantidade de modelos de questões possível.
O título do tema pode causar estranheza, porém, ao menos um segmento, também é estudado no ensino médio. Quando falamos de medidas de posição, estamos tratando de conceitos como média, mediana e moda. Sim, aqueles mesmos conceitos que são cobrados no vestibular. O “algo a mais” cobrado no mundo dos concursos são as medidas de dispersão: variância e desvio padrão.
Enquanto é relativamente simples visualizar em um gráfico as medidas de posição, isso não acontece com as de dispersão. Isso traz um maior grau de abstração ao tema, o que costuma trazer dificuldades de aprendizado a alguns candidatos. Os dois tipos de medidas são utilizados em praticamente todos os temas mais à frente da disciplina. Dessa forma, é essencial que haja sedimentação desses conceitos para possibilitar a resolução de questões dos temas 3) a 6).
Aqui começam os temas mais temidos em como estudar Estatística. A utilização das distribuições de probabilidade varia dependendo de seu intuito. Num caso em que o objetivo é avaliar a probabilidade de ocorrência de “x” sucessos em um intervalo de medida “t”, utiliza-se a distribuição de Poisson.
Quando um experimento se caracteriza pela ocorrência de vários testes consecutivos e independentes, onde o resultado pode ser sucesso ou fracasso, apenas, em cada um deles, utiliza-se a distribuição Binomial.
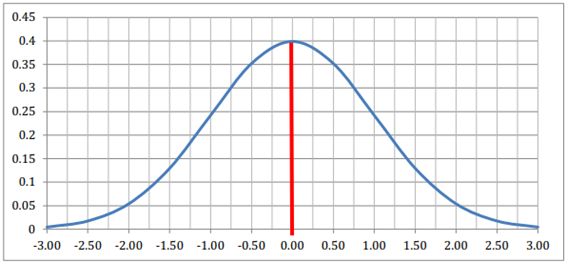
É importante que o aluno correlacione a situação descrita no enunciado da questão e a distribuição correta a ser utilizada. É comum que os editais evidenciem alguns tipos de distribuições em seus conteúdos programáticos. A mais corriqueira é a distribuição de Gauss/Normal.
Temos um grau de abstração consideravelmente elevado quando buscamos a definição formal de Intervalo de Confiança. Por outro lado, a definição informal nos traz mais próximos a sua contextualização no “mundo real”.
Os intervalos de confiança são usados para indicar a confiabilidade de uma estimativa. Também descrevem quão confiáveis são os resultados de uma pesquisa. Uma pesquisa com intervalo de confiança maior é menos confiável quando em comparação a uma que possui um intervalo de confiança menor. Ou seja, quanto mais estreito for o intervalo de confiança, mais confiável é a pesquisa.
Existem 3 situações distintas e corriqueiramente cobradas, nas quais há de se utilizar fórmulas distintas. Variância conhecida, variância desconhecida e probabilidade P conhecida.
O teste de hipótese trata-se da formulação de suposições a respeito de parâmetros de uma população. Dessa forma, pelas características de uma amostra, faz-se um teste que indicará a validade ou não da suposição formulada. Ou seja, há a suposição de um resultado e, por meio da utilização de fórmulas e parâmetros da situação, verifica-se se esse resultado suposto é verdadeiro ou não.
Um exemplo: uma empresa compra tijolos cuja resistência especificada é de 70 kgf, com desvio padrão de 6 kgf. A compradora necessita verificar se um grande lote de tijolos recebidos atende à resistência mínima de 70 kgf. Essa é a hipótese do problema: resistência maior ou igual a 70 kgf. Para a auxiliar, a compradora escolhe uma amostra desse lote e, a partir da avaliação estatística da amostra, conclui a respeito da hipótese formulada. Tal avaliação é o teste de hipótese, o qual demonstrará se a hipótese formulada será confirmada ou rejeitada.
É interessante notar que os exercícios de testes de hipótese utilizam conceitos de intervalos de confiança. Além disso, também é possível fazer correlações entre as fórmulas utilizadas em ambos assuntos. Tais correlações costumam facilitar suas memorizações.
Correlação refere-se ao parâmetro que mede o grau de relação entre variáveis aleatórias quantitativas. Como exemplo, será que a variável aleatória “número de atendimentos respiratórios nos hospitais” e “número de casos confirmados de COVID-19” possuem alguma relação? Se houver, trata-se de uma relação fraca, média ou forte? Normalmente os editais cobram a correlação do tipo linear simples.
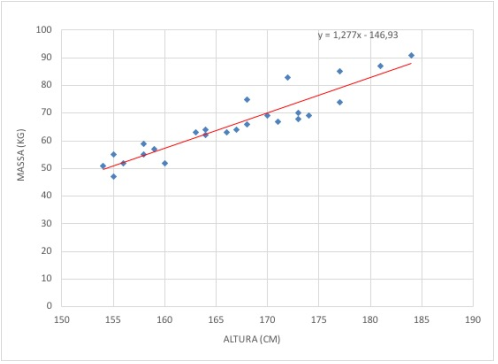
Já a Regressão refere-se à descrição, por meio de uma equação matemática, da relação existente entre variáveis aleatórias. Ou seja, encontra uma equação que consiga descrever a relação entre tais variáveis. É comum que os editais tratem da regressão do tipo linear simples, a qual resulta em equações de primeiro grau.
Após uma contextualização sobre os temas mais pedidos dessa disciplina, passaremos às dicas de como estudar Estatística.
É importante que o candidato tenha o primeiro contato com essa disciplina por bons materiais. Isso diminui as chances de que haja uma sensação de distanciamento do assunto, dificultando sua assimilação. Faz-se necessário que o candidato realize uma autocrítica sincera para escolher entre um material focado em PDFs ou em vídeoaulas.
Para aqueles alunos que já tenham tido contato com Estatística na faculdade ou que possuam muita facilidade em exatas, acreditamos que seja possível dar uma chance aos PDFs. Já para aqueles que não estão incluídos nos grupos citados, as vídeoaulas devem ser um facilitador no estudo da disciplina.
Para que o candidato aproveite o curso, é primordial que preste muita atenção nas resoluções de questões. É importante estar ligado nos conceitos teóricos, mas detectar uma linha de raciocínio nas resoluções é ainda mais essencial. A confecção de um formulário de equações e conceitos deve ocorrer à medida que o aluno acompanha o curso. Ele servirá como repositório teórico em momentos posteriores, primordial no processo de como estudar Estatística.
É muito comum que os alunos pensem que, após terminar um assunto pelo PDF, já sejam mestres naquilo. Inclusive, entendemos que, quando se utiliza um material de qualidade, é comum que essa seja a sensação ao finalizar uma aula. Por outro lado, é imprescindível que o candidato realize uma prova real de seus ensinamentos ao finalizar cada assunto.
É interessante que essa bateria extra seja realizada em um dia distinto ao término da aula. Na aula, o aluno é apresentado ao assunto e tenta entender a lógica da resolução das questões com a ajuda do professor. Pode parecer suficiente, porém, é no momento em que o aluno tenta resolver questões por si só que as dificuldades reais aparecem. Como o assunto acabou de ser estudado, a resolução das dificuldades fica facilitada e proporciona a consolidação do conhecimento. Também é válido que o aluno complemente o seu formulário confeccionado no decorrer da aula.
Seguindo os passos descritos acima com bastante ímpeto, o aluno tende a possuir uma boa base ao término do curso. Além disso, possuirá um formulário que consolida as equações a serem utilizadas e conceitos teóricos basais. Agora é a hora de ficar craque na resolução de questões por assunto!
Lembra quando dissemos acima para estar muito atento ao passo a passo seguido pelo professor na resolução dos exercícios? Com certeza isso ajudou bastante na hora de resolver questões por si só. Agora, a ideia é adaptar esse passo a passo ao seu estilo e entendimento, materializando-o em um resumo/ficha.
Por meio de baterias de questões de um só assunto, o aluno conseguirá detectar um padrão de resolução. Em quais pontos do enunciado buscar certas informações, qual a ordem de utilização das fórmulas que otimiza o tempo, quais as dificuldades mais encontradas. O aluno se defrontará com todas essas questões em suas resoluções e deverá consolidar tudo isso em um documento enxuto.
O próprio processo de confecção do algoritmo de solução, descrito no item acima, já traz um avanço tremendo ao candidato. Além disso, agora também possui um passo a passo, que sempre pode ser consultado e melhorado, muito útil para revisões. Dessa forma, é o momento de o aluno realizar baterias de questões sobre todos os assuntos juntos.
Para que o conhecimento seja consolidado, é muito interessante que os exercícios realizados sejam de um mesmo assunto. Isso faz toda diferença nos estágios mais inicias de como estudar Estatística.
Já num estágio mais avançado, é necessário que o aluno fique mais próximo à situação real de prova. A resolução de questões de assuntos aleatórios aproxima-se do que ocorrerá no dia da prova. Além disso, após o momento em que o candidato atingir um patamar satisfatório de percentual de acertos, cerca de 80%, chega a hora de fazer o controle, cada vez mais intenso, do tempo gasto em cada resolução, trabalhando para o diminuir.
Esperamos que tenham gostado desse panorama sobre como estudar Estatística. Acreditamos que uma contextualização dos temas mais cobrados também auxilie na percepção de como estudar Estatística. Com técnica, perseverança e estratégia você garantirá esses preciosos pontos no seu certame dos sonhos!
Desejo ótimos estudos a todos e um grande abraço.
Caio Castilho.
Assinatura Anual Ilimitada*
Prepare-se com o melhor material e com quem mais aprova em Concursos Públicos em todo o país. Assine agora a nossa Assinatura Anual e tenha acesso ilimitado* a todos os nossos cursos.
ASSINE AGORA – Assinatura Ilimitada
Fique por dentro de todos os concursos: