Fala, pessoal!
Neste artigo, vou ensinar uma maneira muito prática para calcular uma excelente aproximação para a raiz n-ésima de um número p qualquer.
O método que mostrarei a seguir é um caso particular do Método de Newton-Raphson.
Vamos começar com a raiz quadrada para que você possa entender o método. Adaptando o método de Newton-Raphson, obtemos que a raiz quadrada de p pode ser aproximada por:
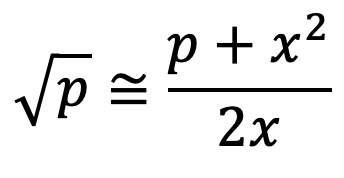
Na fórmula acima, x é uma aproximação qualquer para a raiz quadrada de p.
Exemplo 1: Calcular uma aproximação para √405,4.
Ora, sabemos que √400=20. Assim, podemos usar 20 como uma aproximação inicial para √405,4, ou seja, x = 20. Ficamos com:
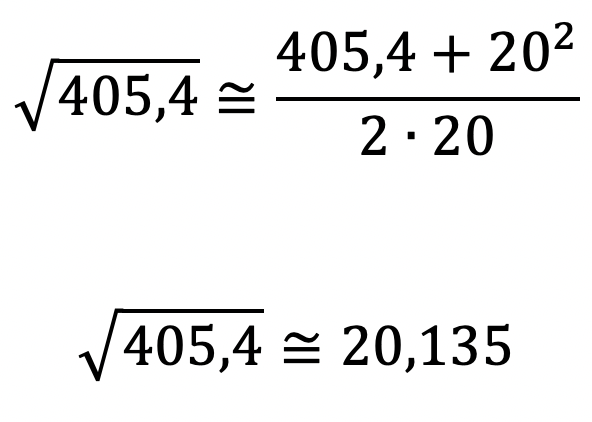
Na calculadora, observamos que o valor exato é 20,13454742… . Obtivemos uma excelente aproximação!!!
Exemplo 2: Calcular uma aproximação para √193.
Ora, sabemos que 142 = 196. Logo, podemos usar x = 14 como aproximação inicial.
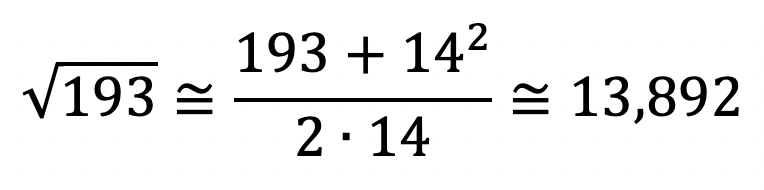
Mais uma excelente aproximação!!! Na calculadora, tem-se que √193 = 13,89244399… .
Vamos agora generalizar. Utilizando o método de Newton-Raphson, fiz uma adaptação para obtermos excelentes aproximações para raízes de qualquer índice. A fórmula é a seguinte:
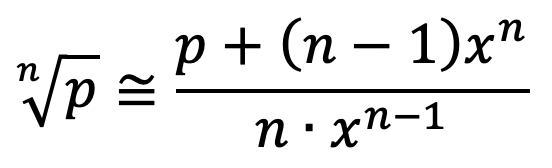
Na fórmula acima, x é uma primeira aproximação para a raiz procurada.
Vamos fazer alguns exemplos para praticar.
Exemplo 3: Calcular uma aproximação para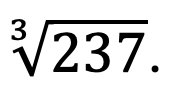 
Ora, sabemos que 63 = 216. Logo, podemos utilizar x = 6 para calcular a aproximação. Temos ainda que n = 3 e p = 237. Ficamos com:
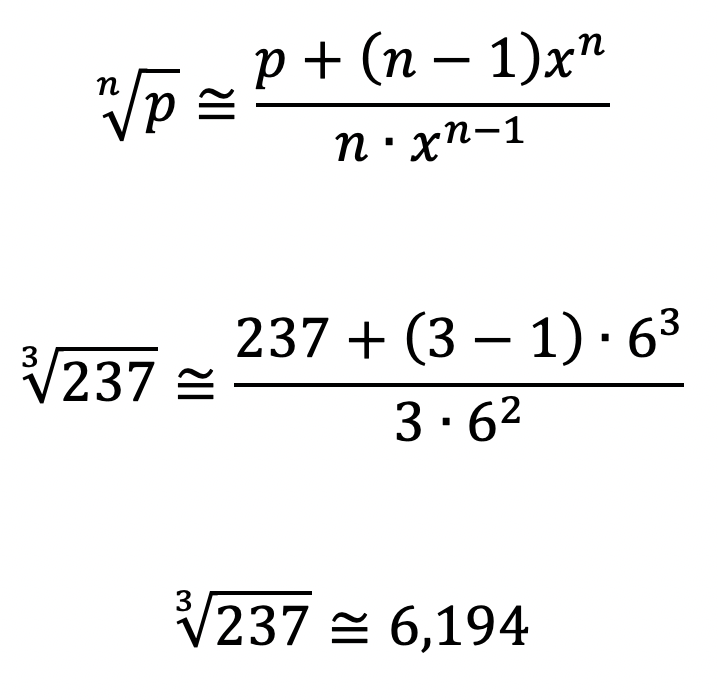
Na calculadora, obtém-se o valor exato de 6,18846…, ou seja, o nosso erro foi de apenas 0,09%.
Exemplo 4: Calcular uma aproximação para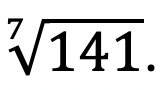 
Sabemos que 27 = 128. Logo, podemos utilizar x = 2 para calcular a aproximação.
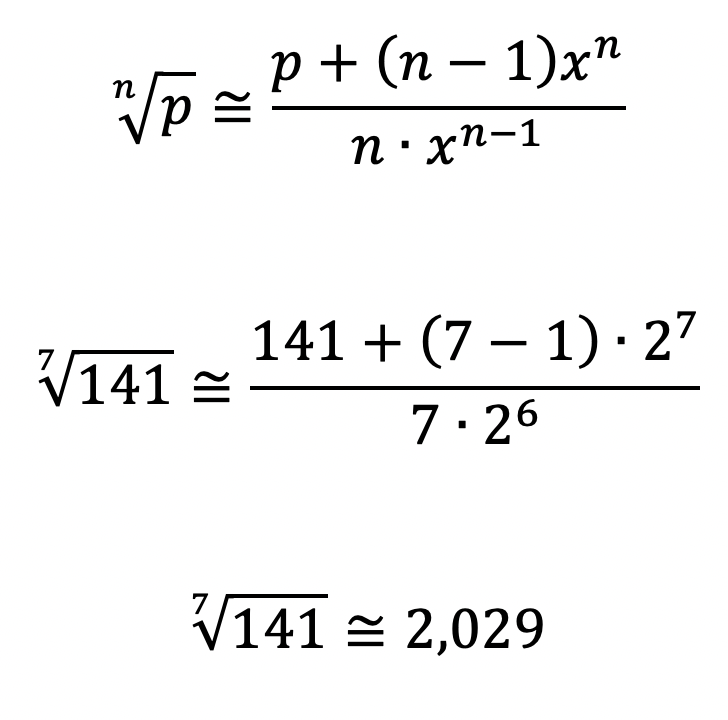
Na calculadora, obtém-se o valor exato de 2,0278…, ou seja, o nosso erro foi de apenas 0,05%.
Veja que o caso anterior da raiz quadrada é apenas um caso particular dessa fórmula geral em que n = 2.
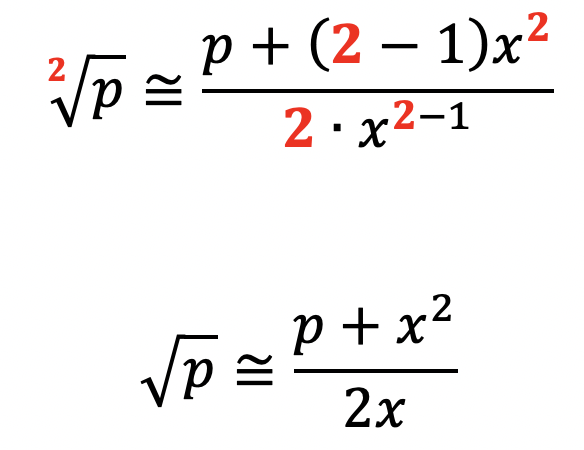
Espero que tenham gostado!
Um forte abraço,
Guilherme Neves