Olá, tudo bem?
Deixo a seguir a resolução de algumas questões da prova de Assistente de Gestão de Políticas Públicas (AGPP) da Prefeitura de São Paulo, realizada no último domingo (08/maio). São questões recentíssimas do CESPE sobre Porcentagens, Conjuntos e Proposições, os três temas principais do edital do concurso do INSS 2016! Embora sejam questões de múltipla escolha, considero muito importante você resolvê-las, para verificar como anda a sua preparação – afinal esta é a banca do seu concurso!!!
E não deixe de ver todos os materiais GRATUITOS para a reta final do INSS 2016 que o Estratégia está disponibilizando – basta CLICAR AQUI!!!
CESPE – PREFEITURA DE SÃO PAULO – 2016) As proposições seguintes constituem as premissas de um argumento.
Assinale a opção correspondente à conclusão que torna esse argumento um argumento válido.
A) Paulo não é técnico de contabilidade e Ana não trabalha na área de informática.
B) Carlos não é especialista em recursos humanos e Paulo não é técnico de contabilidade.
C) Ana não trabalha na área de informática e Paulo é técnico de contabilidade.
D) Carlos é especialista em recursos humanos e Ana trabalha na área de informática.
E) Bianca não é professora e Paulo é técnico de contabilidade.
RESOLUÇÃO:
Temos as premissas:
P1: Bianca não é professora.
P2: Se Paulo é técnico de contabilidade, então Bianca é professora.
P3: Se Ana não trabalha na área de informática, então Paulo é técnico de contabilidade.
P4: Carlos é especialista em recursos humanos, ou Ana não trabalha na área de informática, ou Bianca é professora.
Como P1 é uma proposição simples, começamos por ela, assumindo que Bianca não é professora. Com isso, em P2 vemos que “Bianca é professora” é falso, o que obriga “Paulo é técnico” a ser falso também, de modo a manter essa premissa verdadeira. Assim, temos que Paulo não é técnico de contabilidade. Em P3 vemos que “Paulo é técnico” é F, de modo que “Ana não trabalha” deve ser F também, para manter essa premissa verdadeira. Assim, temos que Ana trabalha na área de informática. Em P4, vemos que “Ana não trabalha” é F, e “Bianca é professora” é F também, o que obriga ser verdade que Carlos é especialista em recursos humanos.
Com as conclusões sublinhadas, podemos marcar a alternativa D.
Resposta: D
Quer receber dicas e materiais gratuitos de Raciocínio Lógico e Matemática para concursos? Basta se inscrever clicando AQUI.
CESPE – PREFEITURA DE SÃO PAULO – 2016) Na cidade de São Paulo, se for constatada reforma irregular em imóvel avaliado em P reais, o proprietário será multado em valor igual a k% de P × t, expresso em reais, em que t é o tempo, em meses, decorrido desde a constatação da irregularidade até a reparação dessa irregularidade. A constante k é válida para todas as reformas irregulares de imóveis da capital paulista e é determinada por autoridade competente.
Se, de acordo com as informações do texto V, for aplicada multa de R$ 900,00 em razão de reforma irregular em imóvel localizado na capital paulista e avaliado em R$ 150.000,00, cuja irregularidade foi reparada em um mês, então a multa a ser aplicada em razão de reforma irregular em imóvel localizado na capital paulista e avaliado em R$ 180.000,00, cuja irregularidade também foi reparada em um mês, será de
A) R$ 1.080,00.
B) R$ 1.350,00.
C) R$ 1.500,00.
D) R$ 1.620,00.
E) R$ 1.800,00.
RESOLUÇÃO:
Foi dito que Multa = k% de P x t. Tivemos uma multa de 900 reais para um imóvel de valor P = 150.000 e atraso de t = 1 mês. Com isso podemos obter o valor de k:
Multa = k% x P x t
900 = k% x 150.000 x 1
k% = 900 / 150.000
k% = 9 / 1500
k% = 3 / 500
k% = 6 / 1000
k% = 0,6 / 100
k% = 0,6 %
Para um imóvel de valor P = 180.000 e atraso de t = 1 mês, temos:
Multa = k% x P x t
Multa = 0,6% x 180.000 x 1
Multa = (0,6/100) x 180.000
Multa = (0,6) x 1800
Multa = 6 x 180
Multa = 1080 reais
Resposta: A
CESPE – PREFEITURA DE SÃO PAULO – 2016) Na cidade de São Paulo, se for constatada reforma irregular em imóvel avaliado em P reais, o proprietário será multado em valor igual a k% de P × t, expresso em reais, em que t é o tempo, em meses, decorrido desde a constatação da irregularidade até a reparação dessa irregularidade. A constante k é válida para todas as reformas irregulares de imóveis da capital paulista e é determinada por autoridade competente.
De acordo com as informações do texto, se foi de R$ 12.000,00 o valor da multa aplicada em razão de reforma irregular em imóvel localizado na capital paulista e avaliado em R$ 1.500.000,00, cuja irregularidade tenha demorado dois meses para ser reparada, então a constante k determinada pela autoridade competente foi igual a
A) 0,40.
B) 0,75.
C) 0,80.
D) 1,25.
E) 1,80.
RESOLUÇÃO:
Foi dito no enunciado que a multa é dada por:
Multa = k% de P x t
Multa = k% x P x t
Temos uma multa de 12.000 reais em um imóvel de valor P = 1.500.000 reais e prazo de t = 2 meses. Assim,
12.000 = k% x 1.500.000 x 2
12.000 = k% x 3.000.000
k% = 12.000 / 3.000.000
k% = 12 / 3.000
k% = 4 / 1.000
k% = 0,4 / 100
k% = 0,4 %
Portanto, k = 0,4.
Resposta: A
CESPE – PREFEITURA DE SÃO PAULO – 2016) Em uma pesquisa relacionada às ações de fiscalização que resultaram em multas aplicadas de acordo com os critérios mencionados no texto, 750 pessoas foram entrevistadas, e 60% delas responderam que concordam com essas ações. Nessa hipótese, a quantidade de pessoas que discordaram, são indiferentes ou que não responderam foi igual a
A) 60.
B) 300.
C) 450.
D) 600.
E) 750.
RESOLUÇÃO:
Como 60% concordam, então as demais pessoas são as 40% restantes. Isto é,
Demais pessoas = 40% de 750
Demais pessoas = 40% x 750
Demais pessoas = 0,40 x 750
Demais pessoas = 4 x 75
Demais pessoas = 300
Resposta: B
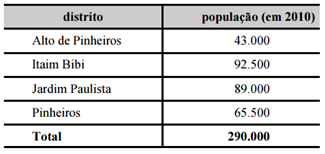
CESPE – PREFEITURA DE SÃO PAULO – 2016) A tabela a seguir, relativa ao ano de 2010, mostra as populações dos quatro distritos que formam certa região administrativa do município de São Paulo.
Considerando-se a tabela apresentada, é correto afirmar que, se, em 2010, um habitante dessa região administrativa tivesse sido selecionado ao acaso, a chance de esse habitante ser morador do distrito Jardim Paulista seria
A) inferior a 21%.
B) superior a 21% e inferior a 25%.
C) superior a 25% e inferior a 29%.
D) superior a 29% e inferior a 33%.
E) superior a 33%.
RESOLUÇÃO:
Temos 290 mil moradores ao todo, sendo que 89 mil são do Jardim Paulista. A chance de selecionar um deles é de P = 89 / 290 = 0,3068 = 30,68%.
Obs.: veja que essa questão envolve uma noção introdutória de Probabilidade. Não acredito que vá cair algo assim no INSS, até porque este assunto não foi solicitado pelo CESPE (para o concurso da Pref. de São Paulo foi exigido).
Resposta: D
CESPE – PREFEITURA DE SÃO PAULO – 2016) Determinado departamento da PMSP recebeu recentemente 120 novos assistentes administrativos. Sabe-se que 70 deles são especialistas na área de gestão de recursos humanos (RH); 50, na área de produção de material de divulgação (MD); e 60, na de administração financeira (AF). Observou-se também que nenhum deles é especialista em mais de duas dessas três atividades; exatamente 25 deles são especialistas tanto em RH quanto em AF e nenhum deles é especialista tanto em AF quanto em MD. Além disso, verificou-se que nenhum deles é especialista em qualquer outra área além dessas três citadas. Com base nessas informações, é correto afirmar que a quantidade de novos assistentes administrativos que são especialistas tanto na área de recursos humanos (RH) quanto na área de produção de material de divulgação (MD) é igual a
A) 5.
B) 15.
C) 25.
D) 35.
E) 45.
RESOLUÇÃO:
Temos os especialistas em RH, em MD e em AF. Portanto, podemos montar esses 3 conjuntos entrelaçados. Com isso, vamos analisar as informações fornecidas, começando pelas mais diretas:
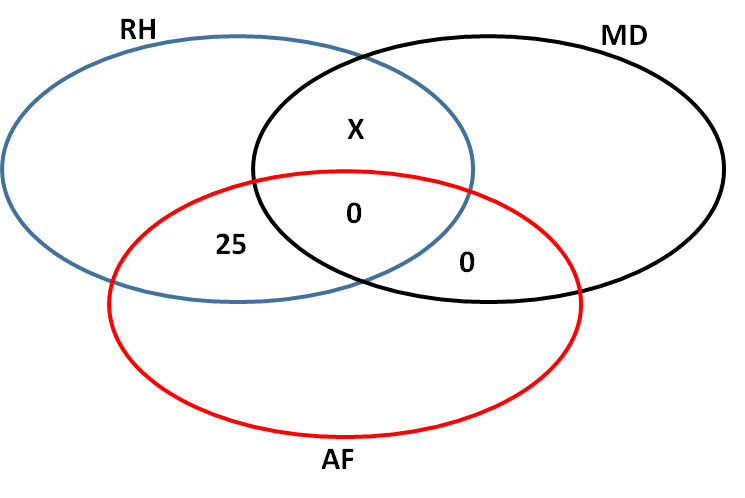
– nenhum deles é especialista em mais de duas dessas três atividades: isso nos mostra que devemos colocar um ZERO no centro do diagrama, na região que representa a interseção dos 3 conjuntos.
– exatamente 25 deles são especialistas tanto em RH quanto em AF: vamos colocar 25 na interseção entre RH e AF, na região que não pertence também ao conjunto MD.
– nenhum deles é especialista tanto em AF quanto em MD: podemos colocar um ZERO na interseção entre AF e MD.
A questão quer saber a interseção entre RH e MD. Portanto, vamos colocar um X nessa região. Até aqui, temos o seguinte diagrama:
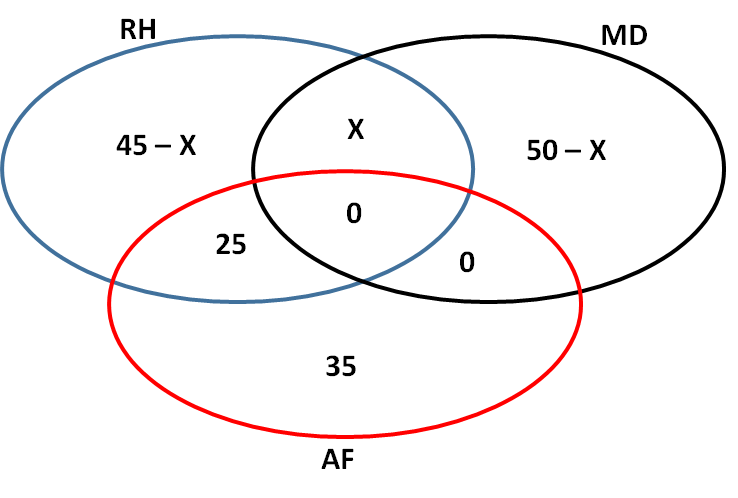
Sabemos que 70 deles são especialistas na área de gestão de recursos humanos (RH). Como já colocamos X, 0 e 25 no conjunto RH, podemos dizer que o número de especialistas APENAS em RH é de:
APENAS RH = 70 – X – 0 – 25
APENAS RH = 45 – X
De forma análoga, o conjunto MD tem 50 elementos. Como já colocamos X, 0 e 0, podemos dizer que APENAS MD = 50 – X – 0 – 0 = 50 – X.
Da mesma forma, o conjunto AF tem 60 elementos. Como já colocamos 25+0+0 = 25, podemos dizer que APENAS AF = 60 – 25 = 35.
Temos a seguinte representação agora:
Como nenhuma das 120 pessoas é especialista em qualquer outra área além dessas três citadas, podemos dizer que a soma dos elementos nos conjuntos acima é igual a 120, ou seja,
120 = 45 – X + 25 + 0 + X + 50 – X + 0 + 35
120 = 155 – X
X = 155 – 120
X = 35
Resposta: D (o gabarito preliminar foi E-45, mas deve ser alterado)