Banco de Dados Descomplicado: Álgebra Relacional.
Introdução
Vamos retomar o nosso estudo em Banco de Dados, uma das áreas de Tecnologia da Informação mais cobradas nas provas dos concursos públicos de alto nível. O assunto de hoje será álgebra relacional.
Além de ser um tema recorrente em provas mais técnicas, que privilegiam o aluno que estudou, a álgebra relacional é uma das bases para o entendimento da SQL (pesadelo de muitos concurseiros). Ademais, você vai reparar que esse tópico não é tão explorado assim.
Como a rotina dos concurseiros é sempre intensa e o estudo precisa ser objetivo, a preferência da maioria dos professores é partir direto para a SQL. Dessa forma, hoje será uma boa oportunidade de você aprender álgebra relacional com calma (ou revisar, se já conhece). Veja o que vamos abordar:
- Contexto da Álgebra Relacional
- Operações Primitivas da Álgebra Relacional
- Operações Derivadas da Álgebra Relacional
- Mapa Mental de Álgebra Relacional
Este artigo é recomendado a todos os concurseiros que fazem provas específicas de TI e aos que estudam para carreiras concorridas na área geral, que cobram a disciplina de Banco de Dados. Se o seu edital cobra SQL, recomendamos fortemente a leitura, a fim de clarear a sua mente.
A fim de compreender este artigo em sua totalidade, o ideal é que você tenha noções básicas de Banco de Dados. Se não souber nada, fique conosco mesmo assim, pois vamos tentar explicar tudo bem “mastigado” a você.
Não recomendamos que você divida a leitura deste artigo em partes, pois os conceitos são interligados. Se não tiver tempo para concluir tudo hoje, então é melhor deixar para outro dia. E aí, está pronto? Vamos começar então.
Tempo de leitura aproximada: 15 a 20 minutos
Contexto da Álgebra Relacional
Antes de mais nada, a álgebra relacional é uma linguagem procedimental / procedural e formal para bancos de dados relacionais. Em outras palavras, o sistema realiza as operações (consultas, atualizações etc.) de acordo com o passo a passo das instruções definidas pelo usuário.
Ao longo do nosso artigo, você vai reparar que algumas operações lembram bastante a Teoria dos Conjuntos, que conhecemos na Matemática (união, diferença, intersecção etc.). Por causa dessa semelhança, é provável que a nomenclatura álgebra tenha sido adotada.
Contudo, ao invés de trabalhar com conjuntos, vamos trabalhar com tabelas. Assim, encare os dados de cada uma das tabelas como se fossem grandes conjuntos. Isso vai facilitar o seu entendimento e a compreensão de como as operações funcionam.
Existem duas grandes categorias de operações da álgebra relacional que são cobradas em concursos: operações primitivas e operações derivadas. Vamos falar em detalhes sobre cada uma delas nas próximas seções.
Cada operação é associada com um símbolo, que também vamos apresentar adiante. Recomendamos fortemente que você os decore, pois isso vai ser determinante para você acertar muitas questões.
Operações Primitivas da Álgebra Relacional
As operações primitivas são consideradas fundamentais. Em outras palavras, elas são consideradas base para outras operações com maior complexidade. Além disso, elas são divididas em dois subgrupos, de acordo com o número de tabelas envolvidas na interação:
Unárias: envolvem apenas uma tabela.
Binárias: envolvem duas tabelas.
As principais operações primitivas da álgebra relacional são projeção, seleção, produto cartesiano, renomeação, união e diferença. Vamos explicar em detalhes cada uma delas.
Atenção: Nem todas as bancas consideram a renomeação como operação primitiva. Dessa forma, se a renomeação não aparecer nas alternativas da sua questão, procure a melhor resposta que contenha as outras cinco operações.
Antes de mais nada, para cada um dos exemplos que vamos apresentar nas próximas subseções, considere que temos inicialmente as seguintes tabelas PROFESSOR e DISCIPLINA e vamos aplicar operações primitivas sobre os seus dados.
| PROFESSOR | ||
|---|---|---|
| id_professor | nome_professor | uf |
| 1 | Felipe Luccas | São Paulo |
| 2 | Adriana Figueiredo | São Paulo |
| 3 | Janaína Arruda | Paraná |
| 4 | Diego Carvalho | Distrito Federal |
| 5 | Raphael Lacerda | Distrito Federal |
| 6 | André Castro | Distrito Federal |
| 7 | Fernando Pedrosa | Distrito Federal |
| DISCIPLINA | |
|---|---|
| id_disciplina | nome_disciplina |
| 1 | Português |
| 2 | Tecnologia da Informação |
Projeção (π)
Primeiramente, a projeção é uma operação unária para selecionar as colunas que contêm os dados de uma tabela, sem fazer restrições. É representada pela letra grega π (pi).
Ex: π nome_professor, uf (PROFESSOR)
| nome_professor | uf |
|---|---|
| Felipe Luccas | São Paulo |
| Adriana Figueiredo | São Paulo |
| Janaína Arruda | Paraná |
| Diego Carvalho | Distrito Federal |
| Raphael Lacerda | Distrito Federal |
| André Castro | Distrito Federal |
| Fernando Pedrosa | Distrito Federal |
Seleção (σ)
Em primeiro lugar, a seleção é uma operação unária que filtra os resultados que satisfaçam uma determinada condição, aplicando uma restrição nos dados. É representada pela letra grega σ (sigma).
Ex: π nome_professor (σ uf = ‘São Paulo’ (PROFESSOR))
| nome_professor |
|---|
| Felipe Luccas |
| Adriana Figueiredo |
Produto Cartesiano (X)
O produto cartesiano é uma operação binária, que seleciona as colunas de duas tabelas de entrada (por isso é considerada binária) com todas as combinações possíveis. É representado pelo sinal de multiplicação X (vezes).
Ex: π nome_professor, uf, nome_disciplina (PROFESSOR X DISCIPLINA)
| nome_professor | uf | nome_disciplina |
|---|---|---|
| Felipe Luccas | São Paulo | Português |
| Felipe Luccas | São Paulo | Tecnologia da Informação |
| Adriana Figueiredo | São Paulo | Português |
| Adriana Figueiredo | São Paulo | Tecnologia da Informação |
| Janaína Arruda | Paraná | Português |
| Janaína Arruda | Paraná | Tecnologia da Informação |
| Diego Carvalho | Distrito Federal | Português |
| Diego Carvalho | Distrito Federal | Tecnologia da Informação |
| Raphael Lacerda | Distrito Federal | Português |
| Raphael Lacerda | Distrito Federal | Tecnologia da Informação |
| André Castro | Distrito Federal | Português |
| André Castro | Distrito Federal | Tecnologia da Informação |
| Fernando Pedrosa | Distrito Federal | Português |
| Fernando Pedrosa | Distrito Federal | Tecnologia da Informação |
Veja que os professores aparecem ministrando disciplinas que não são suas. Isso ocorreu porque usamos o produto cartesiano da álgebra relacional, que efetuou todas as combinações possíveis (mesmo nos casos que não se aplicam), sem nenhuma restrição.
Em outras palavras, o banco de dados não tem inteligência para discernir o que é certo ou errado. Ele faz apenas o que os usuários solicitam. Nesse caso, combinar as tabelas PROFESSOR e DISCIPLINA não é aplicável, pois os professores não ministram todas as disciplinas.
Em contrapartida, poderíamos combinar os professores com os turnos do dia, considerando que eles podem dar aulas no período da manhã, da tarde ou da noite. Faria muito mais sentido no contexto apresentado.
Renomeação (ρ)
Antes de mais nada, a renomeação é uma operação unária para alterar os nomes das tabelas. É útil para as situações em que temos um resultado proveniente de uma operação muito extensa e precisamos representá-lo, de alguma forma. Na prática, é representada pela letra grega ρ (rho).
Ex: ρ RESULTADO (π nome_professor, uf (PROFESSOR))
| RESULTADO | |
|---|---|
| nome_professor | uf |
| Felipe Luccas | São Paulo |
| Adriana Figueiredo | São Paulo |
| Janaína Arruda | Paraná |
| Diego Carvalho | Distrito Federal |
| Raphael Lacerda | Distrito Federal |
| André Castro | Distrito Federal |
| Fernando Pedrosa | Distrito Federal |
União (U)
Primeiramente, a união é uma operação binária que exibe todas as linhas da primeira tabela, seguida de todas as linhas da segunda tabela. Caso haja alguma linha repetida, ela será desconsiderada. Na prática, é representada pelo sinal de adição U (união).
Ex: A = ρ A (π nome_professor (σ uf = ‘Paraná’ (PROFESSOR)))
B = ρ B (π nome_professor (σ uf = ‘Distrito Federal’ (PROFESSOR)))
A U B = (ρ A (π nome_professor (σ uf = ‘Paraná’ (PROFESSOR)))) U (ρ B (π nome_professor (σ uf = ‘Distrito Federal’ (PROFESSOR))))
| nome_professor |
|---|
| Janaína Arruda |
| Diego Carvalho |
| Raphael Lacerda |
| André Castro |
| Fernando Pedrosa |
Observe que não necessariamente as tabelas envolvidas precisam ser diferentes. No exemplo acima, trabalhamos somente com a tabela PROFESSOR.
Ou seja, nós aplicamos projeção e seleção no conjunto A, depois aplicamos projeção e seleção no conjunto B e, por fim, unimos os resultados (A U B). Como explicamos anteriormente, os conjuntos resultantes A e B são as tabelas. Veja se agora ficou mais fácil de entender.
Diferença (-)
Em primeiro lugar, a diferença é uma operação binária que exibe todas as linhas da primeira tabela, excluída de todas as linhas da segunda tabela. Assim como a união, lembra bastante a manipulação com os conjuntos. Na prática, é representada pelo sinal de menos – (diferença).
Ex: A = ρ A (π nome_professor (σ uf = ‘Paraná’ (PROFESSOR)))
B = ρ B (π nome_professor (σ uf = ‘Distrito Federal’ (PROFESSOR)))
A – B = (ρ A (π nome_professor (σ uf = ‘Paraná’ (PROFESSOR)))) – (ρ B (π nome_professor (σ uf = ‘Distrito Federal’ (PROFESSOR))))
| nome_professor |
|---|
| Janaína Arruda |
Da mesma forma que a união, não necessariamente as tabelas envolvidas precisam ser diferentes. O que precisa ser diferente são os conjuntos resultantes da manipulação (A e B).
Operações Derivadas da Álgebra Relacional
As operações derivadas são constituídas a partir de manipulações das operações primitivas que vimos na seção anterior. As principais operações derivadas da álgebra relacional são intersecção, divisão e junção (todas elas binárias). Vamos explicar em detalhes cada uma delas.
Antes de mais nada, para cada um dos exemplos que vamos apresentar nas próximas subseções, considere que temos as tabelas PROFESSOR, DIA_SEMANA e ESCALA_GRAVACAO e vamos aplicar operações derivadas sobre os seus dados.
Se você não está muito familiarizado com Banco de Dados, considere hipoteticamente que a tabela ESCALA_GRAVACAO contém os dias da semana em que cada professor está autorizado a gravar (supondo que cada um grave obrigatoriamente em dias fixos).
| PROFESSOR | ||
|---|---|---|
| id_professor | nome_professor | uf |
| 1 | Felipe Luccas | São Paulo |
| 2 | Adriana Figueiredo | São Paulo |
| 3 | Janaína Arruda | Paraná |
| 4 | Diego Carvalho | Distrito Federal |
| 5 | Raphael Lacerda | Distrito Federal |
| 6 | André Castro | Distrito Federal |
| 7 | Fernando Pedrosa | Distrito Federal |
| DIA_SEMANA | |
|---|---|
| id_dia | nome_dia |
| 1 | Segunda-feira |
| 2 | Terça-feira |
| 3 | Quarta-feira |
| 4 | Quinta-feira |
| 5 | Sexta-feira |
| ESCALA_GRAVACAO | |
|---|---|
| id_professor | id_dia |
| 1 | 2 |
| 1 | 4 |
| 1 | 5 |
| 2 | 1 |
| 2 | 3 |
| 2 | 5 |
| 3 | 1 |
| 3 | 3 |
| 5 | 5 |
| 6 | 2 |
| 6 | 4 |
| 7 | 2 |
| 7 | 4 |
Junção (⋈)
Antes de mais nada, a junção é uma operação binária que fará o relacionamento entre duas tabelas. Em outras palavras, identifica as linhas de uma tabela que estão relacionadas a outra tabela. Na prática, é representada pelo símbolo ⋈ (theta).
Ex: π nome_professor (σ PROFESSOR.id_professor = ESCALA_GRAVACAO.id_professor (PROFESSOR ⋈ ESCALA_GRAVACAO)))
| nome_professor |
|---|
| Felipe Luccas |
| Adriana Figueiredo |
| Janaína Arruda |
| Raphael Lacerda |
| André Castro |
| Fernando Pedrosa |
Observe que são exibidos todos os professores que estão escalados para as gravações, exceto o professor Diego Carvalho (responsável pelos pdfs). Repare que seu identificador nem aparece na tabela ESCALA_GRAVACAO.
A operação junção apresenta algumas variantes. Contudo, as variações não costumam ser muito cobradas pelas bancas no contexto da álgebra relacional. Por este motivo, não vamos aprofundar o conteúdo neste artigo.
Intersecção (∩)
A intersecção é uma operação binária que exibe todas as linhas que estão na primeira e na segunda tabela, ao mesmo tempo. Se você já estudou Teoria dos Conjuntos, em Matemática, então tenha em mente que se trata da mesma operação.
Ex: A = ρ A (π nome_professor (σ PROFESSOR.id_professor = ESCALA_GRAVACAO.id_professor (PROFESSOR ⋈ ESCALA_GRAVACAO))))
B = ρ B (π nome_professor (σ uf = ‘Distrito Federal’ (PROFESSOR)))
A ∩ B = ρ A (π nome_professor (σ PROFESSOR.id_professor = ESCALA_GRAVACAO.id_professor (PROFESSOR ⋈ ESCALA_GRAVACAO)))) ∩ (ρ B (π nome_professor (σ uf = ‘Distrito Federal’ (PROFESSOR))))
| nome_professor |
|---|
| Raphael Lacerda |
| André Castro |
| Fernando Pedrosa |
Este exemplo é um pouquinho mais complicado, mas você vai conseguir entender. Veja que estamos filtrando os professores que estão escalados para as gravações (exemplo que vimos anteriormente, seria a nossa tabela A) e que também estão na UF Distrito Federal (tabela resultante B).
Divisão (÷)
Primeiramente, a divisão é uma operação binária que exibe todos os elementos da primeira tabela que se relacionam com todos os elementos da segunda tabela. Dentre todas as operações que apresentamos hoje, decerto ela é a mais complicada.
Sendo assim, se você entender bem a divisão, pode considerar que está dominando os principais tópicos de álgebra relacional. Vamos ver o último exemplo de hoje.
Ex: A = ρ A (π id_professor, id_dia (ESCALA_GRAVACAO))
B = ρ B (π id_dia (σ DIA_SEMANA.nome_dia = ‘Segunda-feira’ ^ DIA_SEMANA.id_dia = ESCALA_GRAVACAO.id_dia (DIA_SEMANA ⋈ ESCALA_GRAVACAO))))
A ÷ B = ρ A (π id_professor, id_dia (ESCALA_GRAVACAO)) ÷ ρ B (π id_dia (σ DIA_SEMANA.nome_dia = ‘Segunda-feira’ ^ DIA_SEMANA.id_dia = ESCALA_GRAVACAO.id_dia (DIA_SEMANA ⋈ ESCALA_GRAVACAO))))
| id_professor |
|---|
| 2 |
| 3 |
Você Sabia? A álgebra relacional representa os operadores lógicos por meio de sinais. Por exemplo, o e-lógico (and) é representado por ^. Por outro lado, o ou-lógico (or) é representado por v.
Detalhamento
No exemplo, vamos dividir ESCALA_GRAVACAO, representada pela tabela A, por outra tabela que contenha apenas o código da Segunda-feira na tabela DIA_SEMANA, denominada tabela B.
Como a tabela ESCALA_GRAVACAO contempla os campos id_professor e id_dia e vamos dividir por uma tabela que contempla apenas o campo id_dia, a tabela resultante terá apenas o campo id_professor. Pense que a divisão vai “eliminar” o campo repetido, pois tudo ficará mais fácil.
id_professor, id_dia ÷ id_dia = id_professor
Veja que o id_dia da segunda-feira é representado por 1. De acordo com a tabela ESCALA_GRAVACAO, os professores que ministram aulas na segunda-feira são representados pelo id_professor 2 e 3.
Ah, mas representar o professor por código fica feio, não é? Vamos então apresentar o nome do professor por extenso, fazendo uma projeção e uma seleção (agora você já conhece).
Ex: π nome_professor (σ id_professor = 2 v id_professor = 3 (PROFESSOR)))
| nome_professor |
|---|
| Adriana Figueiredo |
| Janaína Arruda |
Mapa Mental de Álgebra Relacional
Chegou o momento mais esperado. Vamos fazer por você algo que nem a sua mãe faria. :) Deixando as piadinhas de lado, preparamos um mapa mental exclusivo de álgebra relacional, a fim de auxiliá-lo nas suas revisões. Aproveite bastante, pois você merece esse mimo!
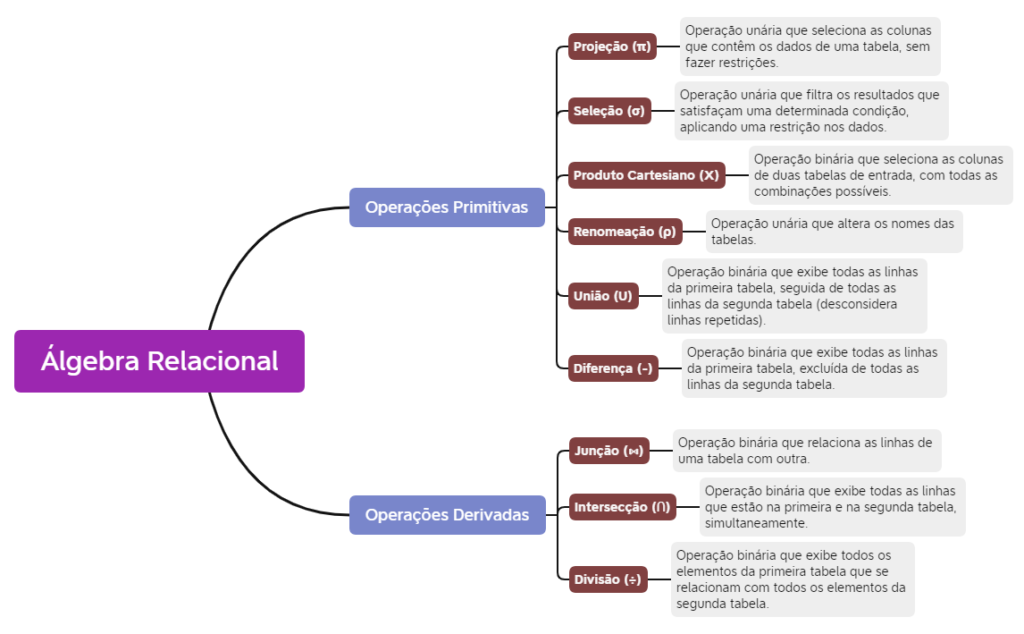
Conclusão
Em suma, apresentamos no artigo de hoje um resumo de álgebra relacional, um dos assuntos mais importantes de Bancos de Dados. Assim, se você leu o artigo na íntegra e entendeu bem os conceitos, o próximo passo agora será realizar muitas questões para treinar.
As questões são a melhor forma de avaliar seu aprendizado. Historicamente, alunos aprovados realizam centenas ou até milhares de exercícios para atingir seu objetivo. O acesso ao Sistema de Questões do Estratégia Concursos é feito pelo link: https://concursos.estrategia.com/.
Não esqueça também de retornar ao tópico periodicamente para fazer revisões. Aproveite o mapa mental disponibilizado neste artigo para isso, pois irá ajudá-lo muito. Caso prefira, você poderá também salvar este artigo nos Favoritos do seu navegador para ler e reler quantas vezes quiser.
Por fim, se você quiser aprofundar o conteúdo ou tirar dúvidas específicas, busque o material do Estratégia Concursos. Nós oferecemos diversos cursos em pdf, videoaulas e áudios para você ouvir onde quiser.
Bons estudos e até a próxima!
Cristiane Selem Ferreira Neves é Bacharel em Ciência da Computação e Mestre em Sistemas de Informação pela Universidade Federal do Rio de Janeiro (UFRJ), além de possuir a certificação Project Management Professional pelo Project Management Institute (PMI). Já foi aprovada nos seguintes concursos: ITERJ (2012), DATAPREV (2012), VALEC (2012), Rioprevidência (2012/2013), TJ-RJ (2022) e TCE-RJ (2022). Atualmente exerce o cargo efetivo de Especialista em Previdência Social – Ciência da Computação no Rioprevidência, além de ser colaboradora do Blog do Estratégia Concursos.