Artigo

Resumo da Análise Combinatória ISS-BH – Estatística

Olá, pessoal. Tudo certo? No artigo de hoje veremos o Resumo da Análise Combinatória ISS-BH.

Basicamente podemos dizer que a Análise Combinatória é o estudo da contagem de elementos finitos, base para a Teoria da Probabilidade.

Assim, vamos conhecer os principais pontos desse tema.

Sem mais delongas, vamos lá.

Princípios Fundamentais da Contagem

Dando início ao Resumo da Análise Combinatória ISS-BH, vamos ver os dois principais princípios da contagem.

Princípio Multiplicativo (multiplicação): ocorre quando os eventos são concomitantes (ocorre um E outro) -> m x n …

Exemplo: (VUNESP/2019 – Prefeitura de dois Córregos/SP) Em um grupo de pessoas, há 12 homens e 13 mulheres. Com essas pessoas, uma dupla será aleatoriamente formada, com um homem e uma mulher, para participar de um concurso. O número total de possibilidades para a formação dessa dupla é igual a

12 x 13 = 156 duplas possíveis

Contagem de Divisores: basta fatorar e utilizar a seguinte fórmula – Número de Divisores = (expoente1 + 1) x (expoente2 + 1) …

Exemplo: número de divisores de 60

60 = 2² + 3¹ + 5¹

Utilizando a fórmula

(2 + 1) x + (1 + 1) + (1 + 1) = 12

Princípio Aditivo (soma): ocorre quando os eventos são mutuamente exclusivos (ocorre um OU outro) -> m + n

Exemplo: (2017 – Conselho Regional de Educação Física/CE) Numa estante encontram-se 4 dicionários de inglês, 3 de espanhol e 2 de francês. De quantas maneiras uma pessoa pode escolher dois dicionários dessa estante e que sejam de idiomas diferentes?

Teremos que:

– um livro de inglês e um de espanhol; ou

– um livro de inglês e um de francês; ou

– um livro espanhol e um de francês.

(4 x 3) + (4 x 2) + (3 x 2) = 26

Permutação

Dando continuidade ao Resumo da Análise Combinatória ISS-BH, vamos revisar a permuta.

Permutação é a técnica que permite calcular as diferentes possibilidades de se ordenar elementos (trocar elementos de lugar)

É muito comum associar a permuta a filas de pessoas ou objetos.

Vamos conhecer os principais tipos de permutação que são cobrados em prova.

Permutação simples: Quantidade de maneiras de reordenar elementos distintos entre si.

Pn = n!

Exemplo: (FGV/2019 – Prefeitura de Salvador/BA) Trocando-se a ordem das letras da sigla PMS de todas as maneiras possíveis, obtêm-se os anagramas dessa sigla. O número desses anagramas é:

P3 = 3! = 6 ou simplesmente 3 x 2 x 1 = 6

Permutação com repetição: Quantidade de maneiras de reordenar n elementos, dos quais k elementos são repetidos.

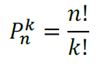
Exemplo: (VUNESP/2019 – Prefeitura de Cerquilho/SP – Adaptada) Com as letras F, F, G e G, o número de agrupamentos diferentes de quatro letras é

P = 4! / 2! 2!

P = 4 x 3 x 2 / 2 x 2

P = 6

Permutação circular: Quantidade de maneiras de reordenar elementos dispostos em círculo,

PCn = (n – 1)!

Exemplo: (2019 – Prefeitura de Ibiaçá/RS) O número máximo de maneiras distintas que um grupo de cinco amigos pode se sentar ao redor de uma mesa circular para realizar um lanche coletivo é:

PC5 = (5 – 1)!

PC5 = 4! = 24

Arranjo

O arranjo representa a seleção de elementos com importância de ordem. Lembre-se disso!

Vamos dividir o arranjo em dois.

Arranjo sem repetição: Quantidade de maneiras de sortear elementos (k) sem repetição dentre todos os elementos (n), de modo que a ordem do sorteio importe.

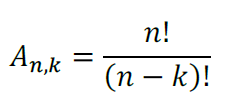
Resumo da Análise Combinatória ISS-BH – Estatística — Fórmula – Arranjo sem repetição

Exemplo: (VUNESP/2019 – Prefeitura de Cerquilho/SP) Na bilheteria de um teatro há apenas 5 ingressos à venda para a seção de uma peça. Se 4 amigos comprarem ingressos para essa seção, então o número total de posições distintas em que esses amigos poderão se acomodar no teatro é

A = 5! / (5 – 4)!

A = 5! / 1!

A = 120

Arranjo com repetição: Quantidade de maneiras de sortear elementos (k) com repetição dentre todos os elementos (n), de modo que a ordem do sorteio importe.

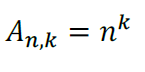
Combinação

A Combinação também busca a seleção de elementos, entretanto diferentemente do arranjo, não há importância de ordem.

Não confunda:

Arranjo -> Ordem faz diferença
Combinação -> Ordem não faz diferença

Assim, para saber de qual estamos tratando é necessário avaliar o contexto da questão.

Combinação simples: Quantidade de maneiras de sortear elementos (k) com repetição dentre todos os elementos (n), de modo que a ordem do sorteio não importe.

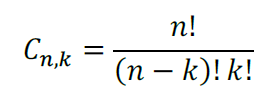
Exemplo: (FGV/2019 – Pref. Angra dos Reis/RJ) Maria possui em casa quatro tipos de frutas: banana, mamão, abacate e manga. Ela decidiu fazer uma vitamina com duas dessas frutas, batendo-as juntas com leite no liquidificador. O número de vitaminas diferentes que Maria poderá fazer é

C = 4! / (4 – 2)! x 2!

C = 4! / 2! x 2!

C = 4 x 3 x 2 / 2 x 2

C = 6

Obs.: A combinação de 0 elemento em n elementos Cn,0 é igual a 1.

Combinação completa: Quantidade de maneiras de sortear sem importância de ordem, p objetos (ex: potes de sorvete), quando há n tipos diferentes (ex: marcas de sorvete).

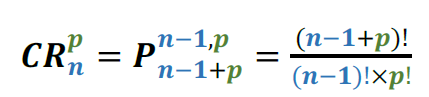
Essa aqui é um pouco mais complicada de entender, vamos ver por meio de um exemplo.

Exemplo: CEBRASPE (CESPE) – Técnico Tributário da Receita Estadual (SEFAZ RS)/2018 – Se 7 kg de feijão forem distribuídos para até quatro famílias, de modo que cada uma delas receba um número inteiro de quilos, então, nesse caso, a quantidade de maneiras distintas de se distribuírem esses 7 kg de feijão para essas famílias será igual a

CR = (4 – 1 + 7)! / (4 – 1)! x 7!

CR = 10! / 3! X 7!

CR = 10 x 9 x 8 x 7 / 3 x 2! X 7!

CR = 5 x 3 x 8

CR = 120

Considerações Finais

Pessoal, chegamos ao final do Resumo da Análise Combinatória ISS-BH. Espero que o artigo tenha sido efetivo para seu aprendizado.

Obviamente trata-se de um resumo apenas com os pontos principais da matéria, tendo outros temas correlacionados como a Partição e Lemas de Kaplansky, assim não deixe de acompanhar as aulas para o aprofundamento necessário.

Ainda, ressaltamos mais uma vez a importância de praticar por exercícios, assim faça muitas questões pelo nosso sistema de questões.

Sistema de Questões (SQ) – Estratégia Concursos

Gostou do artigo? Não deixe de seguir

https://www.instagram.com/resumospassarin/