Resumo sobre Amostragem para o ISS-BH – Estatística
Olá, pessoal. Tudo certo? No artigo de hoje veremos o Resumo das Amostragem para o ISS-BH.
Trata-se de um tema relativamente tranquilo, mas que pode garantir alguns pontos em prova, assim não vamos vacilar.
Tópicos que serão vistos:
- Teoria da Amostragem
- Conceitos Iniciais
- Tipos de Amostragem
- Leis dos grandes números
Sem mais delongas, vamos lá!
Teoria da Amostragem
Vamos iniciar o Resumo das Amostragem para o ISS-BH.
A amostragem faz parte da Estatística Inferencial, ou seja, busca-se tirar conclusões (inferir) sobre um todo (população) a partir de parte dessa população (amostra).
Assim, é importante conhecer alguns conceitos.
- Parâmetro populacional: característica numérica da população Ex. Peso de uma população
- Parâmetro de estimativa (estatística da amostra): medida correspondente feita na amostra Ex. Peso da amostra dessa população
- Inferência: as conclusões feitas a partir da amostra
Etapas: Seleciona a amostra => Calcular a estatística da amostra => Inferir o parâmetro populacional
Conceitos Iniciais
Vamos dar continuidade ao Resumo das Amostragem para o ISS-BH por alguns conceitos.
População: conjunto de elementos que apresenta pelo menos uma característica em comum
Amostra: subconjunto da população, ou seja, conjunto não vazio e que não contém todos elementos.
Assim, da população retiramos a amostra, com essa podemos inferir sobre a população (parâmetro populacional) a partir do estimador do parâmetro populacional.
É importante perceber que o valor da amostra varia, uma vez que a amostra não é sempre a mesma, nesse sentido haverá um erro amostral natural do processo.
Tipos de Erros
Erros Amostrais: são controláveis e mensuráveis
- São intrínsecos a amostragem
- Reduzem com o aumento do número de elementos na amostra
Erros não Amostrais (Sistemáticos): não controláveis -> falha do processo
- Decorrem de falhas no processo de amostragem
- Existem ainda que toda a população seja analisada
Entretanto, é importante não confundir erro amostral com viés do estimador.
Não confunda:
- Viés do estimador (vício ou tendência) = diferença entre o seu valor esperado e o verdadeiro valor do parâmetro
- Erro amostral = diferença entre o estimador e o parâmetro populacional
Também é válido lembrar que:
- Unidades amostrais: elementos da população a serem selecionados
- Tamanho amostral: quantidade de elementos da amostra
Tipos de Amostragem
Vejamos agora no Resumo das Amostragem para o ISS-BH sobre os tipos de amostragem.
- Amostragem probabilística: segue métodos rigorosamente científicos, cada elemento tem uma probabilidade conhecida de ser selecionada.
- Amostragem não probabilística: trata-se de uma escolha deliberada do pesquisador.
Compreendido a diferença, vamos a cada uma das hipóteses.
Amostragem probabilística
Vejamos a Amostragem probabilística.
Amostragem probabilística:
- Amostragem Aleatória Simples (casual): sorteio de um elemento, assim todos os elementos possuem a mesma probabilidade (p) de serem selecionados.
p = n/N
Peso amostral = inverso da probabilidade (p)
- Amostragem Sistemática: amostradas são extraídas periodicamente (R), por exemplo, de 5 em 5 elementos.
R = N (população) / n (número de elementos da amostra)
Obs.: Utiliza-se a parte inteira de R.
- Amostragem Múltipla: as amostras são extraídas em etapas sucessivas (de forma sequencial)
- Amostragem por Estratificação: dividir a população em estratos (subpopulações) para que os estratos sejam homogêneos (baixa variabilidade).
Em seguida, é realizada uma técnica de amostragem simples para selecionar os elementos de cada estrato.
Os estratos não precisam ser do mesmo tamanho, e a amostra pode ser do mesmo tamanho (amostragem uniforme) ou proporcional ao tamanho do estrato (amostragem proporcional)
Também é possível encontrar a amostragem ótima (de Neyman), que depende tanto do tamanho populacional, quanto da sua variabilidade (desvio padrão), assim há o menor erro amostral entre elas.
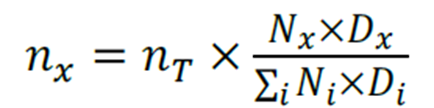
- Amostragem por Conglomerados: dividir a população em conglomerados (cluster) para que os conglomerados sejam heterogêneos (alta variabilidade), ou seja, cada cluster representa toda a população.
Muitas questões buscam tentar confundir o candidato referente a amostragem por estratificação e por conglomerado, então vejamos.
Não confunda:
- Estratificação: o macro é diferente (heterogêneo), micro é igual (homogêneo). Ex: AAA; BBB; CCC

- Conglomerado: o macro é igual (homogêneo), micro é diferente (heterogêneo). Ex: ABC; ABC; ABC

Amostragem não probabilística
Agora vamos conhecer a Amostragem não probabilística.
Amostragem não probabilística:
- Amostragem por Conveniência: pela conveniência do pesquisador, não havendo critérios científicos.
- Amostragem por Julgamento: seleção por critérios definidos pelo arbítrio (julgamento) do entrevistador.
- Amostragem por Cotas: selecionam pelas mesmas proporções da população, de forma não probabilística.
- Amostragem por Tipicidade: seleciona-se elementos representativos da população, assim é necessário que haja conhecimento prévio da população.
- Amostragem por Voluntários: próprios indivíduos da população se voluntariam para participar da pesquisa.
- Amostragem por Bola de Neve: o pesquisador seleciona alguns indivíduos e esses convidam outros participantes. Atente-se que pela falta de controle, há uma tendência de baixa representação populacional.
Leis dos grandes números
Para finalizar o Resumo Sobre Amostragem para o ISS-BH, vamos conhecer as Leis dos Grandes Números. Comecemos pelo seu enunciado:
“A média aritmética dos valores observados tendem à esperança da variável aleatória, com o aumento do número de observações.”
Em outras palavras, a média amostral converge para a média populacional (valor esperado) com o aumento da amostra, afinal a amostra fica cada vez mais parecida com a população.
Podemos separar a Lei dos grandes números em duas.
- Lei Fraca dos grandes números: a média amostral converge para a média populacional conforme o aumento da amostra. Em outros termos, a partir de um determinado “n”, a convergência é provável;
- Lei Forte dos grandes números: a média amostral converge quase certamente para o seu valor esperado com o aumento da amostra. Em outros termos, a partir de um determinado “n”, a convergência é certa ou quase certa.
Obs.: As Leis dos Grandes Números tratam da convergência da média amostral à média populacional (que é um número) e não da distribuição de uma variável aleatória.
Forte X Fraca
Lei Fraca: Convergência é provável -> Fraco/pequeno: é apenas probabilidade
Lei Forte: Convergência é certa (quase certa) –> Quem é forte ganha quase de forma certa
Considerações Finais
Pessoal, chegamos ao final do Resumo sobre Resumo de Variáveis Aleatórias Contínuas ISS-BH. Espero que o artigo tenha sido efetivo para seu aprendizado.
Obviamente trata-se de um resumo apenas com os pontos principais da matéria, assim não deixe de acompanhar as aulas para o aprofundamento necessário.
Ainda, ressaltamos mais uma vez a importância de praticar por exercícios, assim faça muitas questões pelo nosso sistema de questões.
Sistema de Questões (SQ) – Estratégia Concursos
Gostou do artigo? Não deixe de seguir
https://www.instagram.com/resumospassarin/
Cursos e Assinaturas
Prepare-se com o melhor material e com quem mais aprova em Concursos Públicos em todo o país.
Até mais e bons estudos!