Resumo sobre Teste de Hipóteses para ISS-BH – Estatística
Olá, pessoal. Tudo certo? No artigo de hoje veremos o Resumo sobre Teste de Hipóteses para ISS-BH.
Os assuntos que serão tratados:
- Conceitos Fundamentais
- Teste de Hipótese para Média
- Teste de hipóteses para proporções
- P-Valor
Assim, vamos lá.
Conceitos Fundamentais
Vamos iniciar o Resumo sobre Teste de Hipóteses para ISS-BH pelos Conceitos Fundamentais.
- Hipótese nula (H0) = Aquela que está sendo testada.
- Hipótese alternativa (H1) = Hipótese que contraria a Hipótese nula, ou seja, a hipótese nula é falsa.
Inicialmente considera-se a hipótese nula como verdadeira e se construí um intervalo de confiança em torno do parâmetro.
O intervalo de confiança representa os limites para rejeitar ou aceitar a hipótese. Vejamos graficamente:
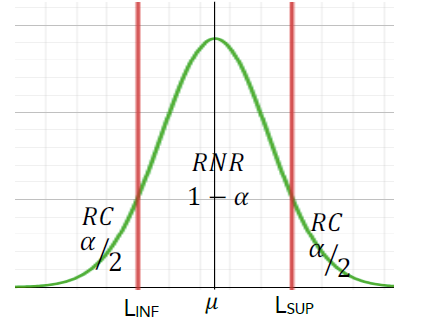
Do gráfico podemos entender que:
- Resultado do Teste na Região Crítica (RC) -> Rejeitar H0
- Resultado do Teste na Região de Não Rejeição (RNR) -> Não Rejeitar H0
É válido lembrar que o teste de hipótese pode ser bilateral, unilateral à esquerda e unilateral à direita.
- Teste bilateral: Região Crítica dividida nos 2 extremos -> H0 ≠ dos limites
- Teste unilateral à esquerda: Região Crítica somente à esquerda -> H0 < dos limites
- Teste unilateral à direita: Região Crítica somente à direita -> H0 > dos limites
Numa situação das medidas de uma peça para uma máquina, por exemplo, faz sentido imaginar que o teste seja bilateral (a peça não pode ser nem menor e nem maior que determinado limite).
Agora imagine que você esteja comprando matéria-prima, o que vai importar é o Teste unilateral à esquerda, pois você não quer receber menos que o limite, mas se tiver a mais não tem problema, não é mesmo?
Tipos de Erro
Dando continuidade ao Resumo sobre Teste de Hipóteses para ISS-BH, vamos adentrar nos Tipos de Erro.
- Erro tipo I (probabilidade α): rejeitar H0 dado que H0 é verdadeira -> “não acreditar no inocente”
- Erro tipo II (probabilidade β): não rejeitar H0 dado que H0 é falsa -> “acreditar no bandido”
Importante saber que os erros do tipo I e II não guardam relação direta, ou seja, os erros não são complementares (α + β ≠ 1)
Vamos sumarizar por meio de uma tabela
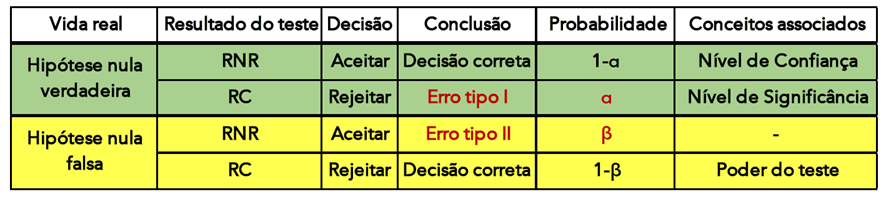
Teste de Hipótese para Média
Agora vamos adentrar no principal Teste de Hipótese, o teste para média.
Para isso é necessário fazer algumas perguntas “para o exercício”.
- A variância/desvio padrão populacional é conhecida?
Se sim, temos que:
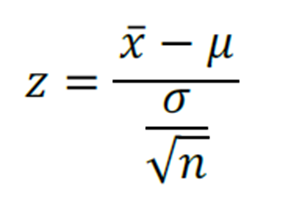
(Média amostral – média populacional) / (desvio padrão populacional / raiz da amostra)
Exemplo: (IBFC/2020 – EBSERH) Uma empresa que produz parafusos verificou que a espessura dos parafusos que produz segue uma distribuição aproximadamente normal com média de 4,82 cm e variância de 16 cm 2. Após a queda de energia num certo período, deseja-se verificar se houve alteração na espessura dos parafusos produzidos. Se numa amostra de 16 parafusos verificou-se que a espessura média dos parafusos acusou média de 4,5 cm, assinale a alternativa que apresenta o valor da estatística teste padrão.
Z = 4,5 – 4,82 / (4 / (raiz 16)
Z = -0,32 / (4/4)
Z = -0,32
Se não, devemos fazer outra pergunta.
- A população é maior ou igual a 30?
Se sim, utilizaremos a fórmula vista anteriormente, entretanto já que não temos o desvio padrão populacional, utilizaremos o amostral (s).
Agora se a resposta for não, utilizaremos o t de Student:
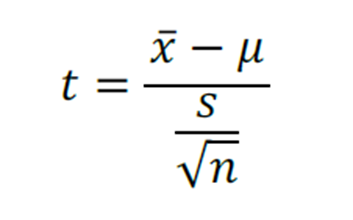
Para consultar na tabela t de Student, devemos utilizar o número de graus de liberdade.
Graus de liberdade: n -1
Exemplo t de Student
É válido ver por meio de um exemplo como resolveremos esse tipo de exercício.
Exemplo: (VUNESP/2021 – CA CFO-QC) Uma variável aleatória X apresenta uma população normalmente distribuída e variância desconhecida. Deseja-se testar se a média μ dessa população difere de 20, a um nível de significância α, utilizando a distribuição t de Student. Para isto, extraiu-se uma amostra aleatória, com reposição, da população de tamanho 16, obtendo-se uma média amostral igual a 19,1 e variância 2,25.

Considerando as hipóteses H0: μ=20 (hipótese nula) e H1: μ≠20 (hipótese alternativa), a conclusão é que H0
Vamos iniciar pela fórmula
t = (19,1 – 20) / raiz 2,25 / raiz 16
t = -0,9 / (1,5 / 4)
t = – 2,4
Lembrando que temos como grau de liberdade (G.L)
G.L: 16 – 1
G.L: 15
Consultando a tabela e comparando com o t de Student
- Se o nível de significância for 5% -> T = -2,13 > -2,4 -> Rejeita
- Se o nível de significância for 2,5% -> T = -2,95 < -2,4 -> Não rejeita
Teste de hipóteses para proporções
Os testes de hipóteses para proporções são aplicáveis para populações que seguem distribuições de Bernoulli (sucesso ou fracasso) dada uma proporção p desconhecida.
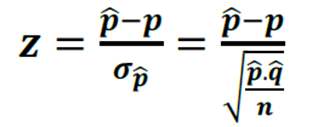
Vamos entender por meio de um exemplo.
Exemplo: (FCC/2012 – ISS SP) Se Z tem distribuição normal padrão, então:
P(Z < 0,84) = 0,80, P(Z < 1,5) = 0,933, P(Z < 1,96) = 0,975, P(Z < 2,5) = 0,994.
Testes realizados pela indústria Cookwell indicam que seu forno de microondas tem probabilidade 0,1 de apresentar a 1a falha antes de 1000 horas de uso. Um novo método de produção está sendo implantado e os técnicos garantem que a probabilidade acima deve diminuir. Com o objetivo de verificar esta afirmação, tomou-se uma amostra de 144 aparelhos e os resultados indicaram 9 com a 1a falha antes de 1000 horas de uso. O valor do nível descritivo do teste, calculado através da proporção amostral, supondo que a mesma tem distribuição aproximadamente normal e não considerando qualquer correção de continuidade, é,
Desvio padrão da proporção amostral pode ser encontrada:
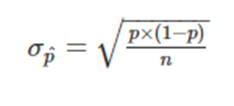
DP = raiz [(0,1 x 0,9) / 144]
DP = 1/40
Sendo a proporção amostral 6,25% (9/144) e a proporção populacional 10%
Z = 6,25 – 10 / (1/40)
Z = -1,5
Do dado do exercício Z = 0,933
Logo,
X = 1 – 0,933
X = 6,7%
P-Valor
O p-valor (probabilidade de significância) é outra forma de avaliar o resultado do teste de hipóteses.
Trata-se da probabilidade de obter um valor igual ao observado ou mais externo.
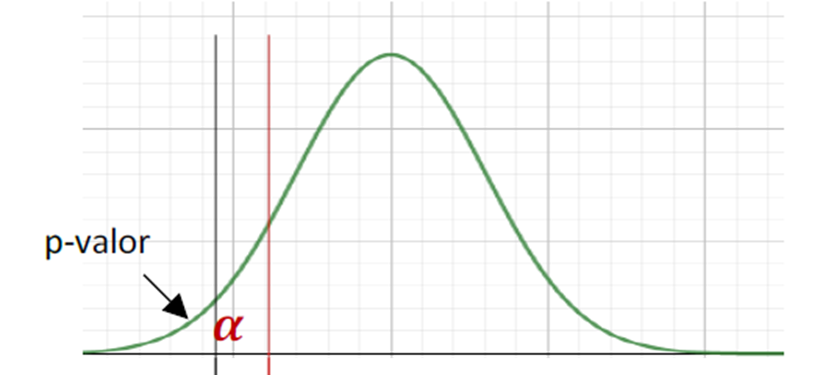
Assim, podemos comparar o p-valor com o nível de significância
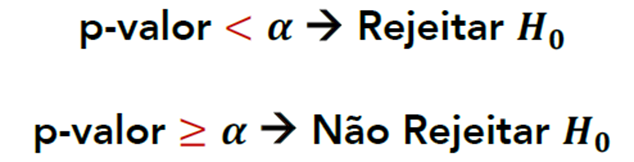
E como encontramos numericamente o p-valor? Basta utilizar a fórmula.
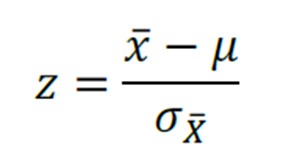
E em sequência consultar em uma tabela de probabilidade ou dado do exercício.
Exemplo: Verificar se há rejeição no teste de hipótese unilateral a esquerda para uma média amostral de 1,85 média populacional de 5 e desvio padrão de 0,1, tendo como nível de significância 5%
Utilizemos a fórmula
Z = (1,85 – 2) / 0,1
Z = -1,5
Vamos consultar na tabela P (0 < Z < z):
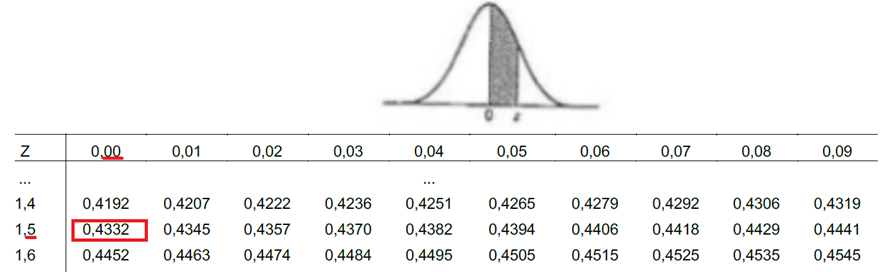
Por simetria -1,5 = 0,4332
Ou seja, 43,32% de probabilidade do valor estar de 0 até o p-valor.
Como só nos interessa verificar a rejeição a esquerda, assim temos que
= 50% – 43,32%
= 6,68%
Assim, nosso p-valor é de 6,68%, ou seja, maior que o nível de significância, não rejeitaremos a hipótese.
Considerações Finais
Pessoal, chegamos ao final dos Resumo sobre Teste de Hipóteses para ISS-BH. Espero que tenham gostado.
Obviamente trata-se de um resumo apenas com os pontos principais da matéria, as aulas são bem aprofundadas em exemplos e exercícios além de assuntos que também são importantes como a testes de hipóteses para a variância, Teste qui-quadrado e testes não paramétricos (Kappa, Wilcoxon e Mann-Whitney), assim não deixe de acompanhar as aulas para o aprofundamento necessário.
A estatística, como as matérias de exatas no geral, só se aprende de fato por meio de muito exercícios, logo deixe de praticar.
Sistema de Questões (SQ) – Estratégia Concursos
Gostou do artigo? Não deixe de seguir
https://www.instagram.com/resumospassarin/
Cursos e Assinaturas
Prepare-se com o melhor material e com quem mais aprova em Concursos Públicos em todo o país.
Até mais e bons estudos!