Resumo das Medidas de Dispersão ISS-BH – Estatística
Olá, pessoal. Tudo certo? No artigo de hoje veremos o Resumo das Medidas de Dispersão ISS-BH.
As medidas de dispersão são divididas em dois grupos, dispersão absoluta e dispersão relativa, tendo como principal cobrança a variância e desvio padrão.
Pronto para revisar? Vamos lá!
Medidas de dispersão
Iniciando o Resumo das Medidas de Dispersão ISS-BH, vamos falar contextualizar.
As Medidas de dispersão (ou variabilidade) são medidas que indicam a variação dos dados de um conjunto
Podemos dividi-las em dois grupos:
Medidas de dispersão absoluta:
- amplitude total;
- amplitude interquartílica;
- desvio médio;
- variância; e
- desvio-padrão.
Vejamos sobre as propriedades da dispersão absoluta.
1ª Propriedade: A soma ou a subtração de uma constante não altera as medidas de dispersão absoluta.
2ª Propriedade: A multiplicação ou a divisão de uma constante altera as medidas de dispersão absoluta.
Medidas de dispersão relativa:
- coeficiente de variação (de Pearson); e
- variância relativa.
Também conheçamos as propriedades da dispersão relativa
1ª Propriedade: A soma ou a subtração de uma constante altera as medidas de dispersão relativa.
2ª Propriedade: A multiplicação ou a divisão de uma constante não altera as medidas de dispersão relativa.
Esquematizemos as propriedades:

Amplitude Total
Sabemos que a amplitude é a diferença entre o valor máximo e mínimo, bem tranquilo.
Apenas destacamos que a amplitude para dados agrupados em classes é encontrada a partir da diferença entre o ponto médio da última classe e da primeira.
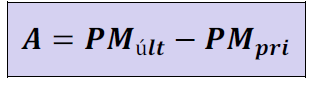
Amplitude interquartílica
Dando continuidade ao Resumo das Medidas de Dispersão ISS-BH, conheçamos a Amplitude interquartílica.
A amplitude interquartílica (distância interquartílica, intervalo interquartílico) é o resultado da subtração entre o 3º quartil e o 1º quartil.
AI = Q3 – Q1
Já a amplitude semi-interquartílica (desvio quartílico) é a metade da amplitude interquartílica.
DQ = (Q3 – Q2) / 2
Assim, lembre-se que “semi” é divido por 2.
Desvio
O Desvio é a distância entre a observação e a medida, destaquemos as duas principais
- Desvio em relação à média – di = x – média
- Desvio em relação à mediana– di = x – Md
Obs.: Quando o desvio é grande, há grande variabilidade dos dados.
Desvio absoluto médio
Já o desvio médio mede a dispersão entre os valores e as médias.
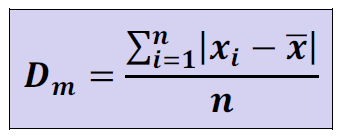
Vejamos um exemplo numérico para facilitar.
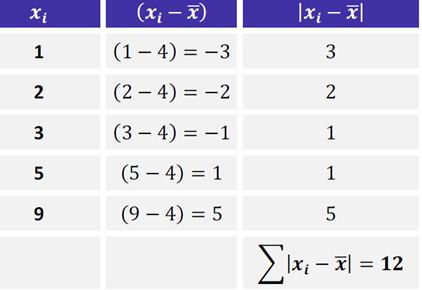
Obs.: Atente-se que buscamos o somatório do módulo dessa diferença.
Dm = 12/5 = 2,4
Variância
A variância basicamente mostra o quão dispersos os dados estão em relação à média. Trata-se da média dos quadrados dos desvios em relação à média.
Vejamos a fórmula da variância populacional (parâmetro populacional) e variância amostral (estimador), respectivamente.

Assim, podemos pensar também que a variância é a diferença entre a média dos quadrados e o quadrado das médias.
Também destacamos a seguinte Propriedade da Variância.
Propriedade: A multiplicação ou a divisão de todos os valores de uma variável por uma constante k é afeta pelo valor quadrado dessa constante.
Exemplos de aplicação
É importante que saibas calcular das duas formas, pois em alguns exercícios faz muita diferença em termos de tempo o método adotado, assim vamos exemplificar a diferença de cálculo por meio de um exemplo.
Dada a população {1, 2, 3, 5, 9}, vamos encontrar a variância populacional das duas formas
Média = (1 + 2 + 3 + 5 + 9) / 5
Média = 20/ 5
Média = 4
Agora vamos calcular pela primeira forma.
VAR = [(1 – 4)² + (2 – 4)² + (3 – 4)² + (5 – 4)² + (9 – 4)²] / 5
VAR = [(-3)² + (-2)² + (-1)² + (1)² + (5)²] / 5
VAR = 9 + 4 + 1 + 1 + 25 / 5 -> atente-se que um número negativo elevado ao quadrado resultado em um número posto
Assim,
VAR = 40/ 5
VAR = 8
Agora utilizaremos o conceito de que a variância é a diferença entre a média dos quadrados e o quadrado das médias.
VAR = [(1² + 2² + 3² + 5² + 9²) / 5] – 4²
VAR = [(1 + 4 + 9 + 25 + 81) / 5] – 16
VAR = (120/ 5) – 16
VAR = 24 – 16
VAR = 8
Já que falamos da variância amostral, vamos encontrá-la utilizando os valores encontrados.
VAR = 40/ 5 – 1
VAR = 40/ 4
VAR = 10
Também podemos simplesmente ajustá-la no final.
VAR = 8 x n / (n – 1)
VAR = 8 x 5 / 4
VAR = 10
Perceba que de qualquer forma que se calcule, o valor encontrado deve ser o mesmo.
Desvio Padrão
Dando continuidade ao Resumo das Medidas de Dispersão ISS-BH, vamos falar sobre o desvio padrão.
Basicamente ele pode ser determinado pela raiz quadrada da variância.
Assim os valores próximos da média darão um desvio padrão pequeno e por ser uma raiz quadrada, o valor sempre será igual ou maior que zero.
Atente-se a diferença entre a propriedade da multiplicação ou divisão de uma constante para o desvio padrão e variância.
Propriedade: A multiplicação ou a divisão de todos os valores de uma variável por uma constante k é afeta pelo valor dessa constante.
Coeficiente de Variação e Variação Relativa
O Coeficiente de Variação mede a variação dos dados em relação à média. A vantagem é que ele pode ser utilizado em conjunto de dados em grandes diferentes, afinal é adimensional.
Podendo ser calculado da seguinte forma:

Regras empíricas:
a) baixa dispersão se CV < 15%;
b) média dispersão se 15% < CV < 30%; ‑
c) elevada dispersão se CV > 30%.
Variância Relativa
Já a variância relativa é utilizada para encontrar o quociente entre a variância absoluta e o quadrado da média, em outros termos, o quadrado do coeficiente de variação.

Considerações Finais
Pessoal, chegamos ao final do Resumo sobre Resumo das Medidas de Dispersão ISS-BH. Espero que o artigo tenha sido útil para sua revisão de estatística.
Obviamente trata-se de um resumo apenas com os pontos principais da matéria, assim não deixe de acompanhar as aulas para o aprofundamento necessário.
Também não deixe de praticar por meio do nosso sistema de questões.
Sistema de Questões (SQ) – Estratégia Concursos
Gostou do conteúdo? Não deixe de seguir
https://www.instagram.com/resumospassarin/
Cursos e Assinaturas
Prepare-se com o melhor material e com quem mais aprova em Concursos Públicos em todo o país.
Até mais e bons estudos!