Gabarito PRF Raciocínio Lógico Matemático (comentado)
Olá, pessoal. Tudo bem? Sou o Eduardo Mocellin, professor de Matemática e de Raciocínio Lógico do Estratégia Concursos.
A seguir, eu e o professor Francisco Rebouças comentamos as questões de Raciocínio Lógico-Matemático da prova da Polícia Rodoviária Federal (PRF) de 2021, bem como o gabarito.
Ressalto que a ordem das questões pode variar de acordo com cada modelo de prova.
Espero que tenham alcançado um bom desempenho :)
Prof. Eduardo Mocellin
Foi modelado que o espalhamento de uma notícia em uma população – entendido como o percentual de indivíduos dessa população que recebe essa notícia por unidade de tempo – é diretamente proporcional ao percentual de indivíduos da população que já conhecem a notícia multiplicado pelo percentual de indivíduos dessa população que ainda não a conhecem até aquele instante. A constante k de proporcionalidade depende, entre outros fatores, do impacto da notícia na vida dos envolvidos e de propriedades dos meios de comunicação disponíveis.
Tendo como base essas informações e considerando que, para certa notícia, k = 1, julgue os itens seguintes.
Antes de julgar os itens da questão, vamos modelar matematicamente o que seria o espalhamento de uma notícia.
Se considerarmos que x é o percentual de pessoas que já conhecem a notícia, temos que 1 – x é o percentual
de pessoas que não conhecem a notícia.
Exemplo: se 10% das pessoas conhecem a notícia, o total de pessoas que não conhecem a notícia é:
1 − x
= 100% − 10%
= 90%
Segundo o enunciado, o espalhamento de uma notícia (E) é dado pelo seguinte produto:

Para o caso em questão, temos k = 1:
E = x. (1 − x)
Agora que entendemos a expressão que modela o espalhamento da notícia, vamos julgar os itens.
27. Se, em determinado instante, 30% da população já conhece a notícia, então, nesse instante, o seu espalhamento estaria em patamar superior a 20% por unidade tempo.
Comentários:
Esse item informa que 30% da população já conhece a notícia, isto é, x = 30%. O espalhamento é dado por:
E = x. (1 − x)
E = 0,3. (1 − 0,3)
E = 0,3 . 0,7
E = 0,21 = 21%
Portanto, o espalhamento é superior a 20%.
Gabarito: CERTO.
28. Se, em determinado instante, o espalhamento de uma notícia é igual a 16% por unidade de tempo, então, nesse instante, mais de 75% da população ainda desconhece a notícia.
Comentários:
Note que, se 80% da população desconhece a notícia (1 − x), temos que 20% da população conhece a notícia
(x). Nesse caso, teríamos um espalhamento de 16%:
E = x. (1 − x)
E = 0,2 × 0,8
E = 0,16 = 16%
Ocorre que, se 20% da população desconhece a notícia (1 − x), temos que 80% da população conhece a notícia (x). Nesse caso, também teríamos um espalhamento de 16%:
E = x. (1 − x)
E = 0,8 × 0,2
E = 0,16 = 16%
Note que não se pode afirmar que, com um espalhamento de 16%, necessariamente mais de 75% da população ainda desconhece a notícia. Isso porque o desconhecimento de 20%, assim como o de 80%, nos dá um espalhamento de 16%. O gabarito, portanto, é ERRADO.
Para obter os valores de 20% e de 80%, poderíamos resolver a seguinte equação do segundo grau que surge ao atribuir E = 16%:
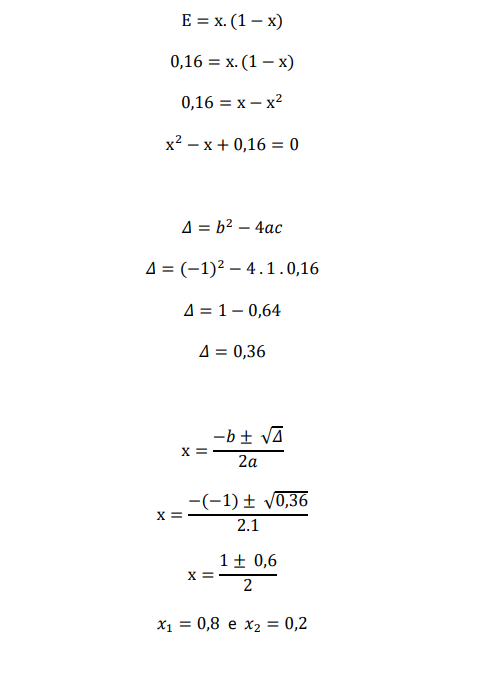
Note que, com um espalhamento de 16%, obtivemos 2 casos de percentual de pessoas que conhecem a notícia (x): 80% e 20%. Para esses dois casos, o percentual de pessoas que desconhecem a notícia (1 − x) é de 20% e de 80%, respectivamente.
Novamente, perceba que um desconhecimento de 20% gera um espalhamento de 16% e, portanto, é errado afirmar que o desconhecimento é necessariamente maior do que 75%.
Gabarito: ERRADO.
29. De acordo com a modelagem realizada, é possível que, em determinado instante, o espalhamento da notícia seja superior a 50% por unidade de tempo.
Observe que o espalhamento é modelado por uma função do segundo grau:
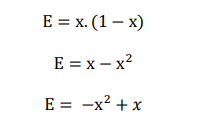
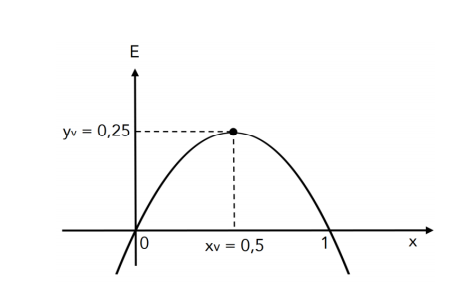
Essa função do segundo grau apresenta concavidade virada para baixo, pois o termo que multiplica x2 é negativo (−1). Nesse caso, a função admite um máximo yv:
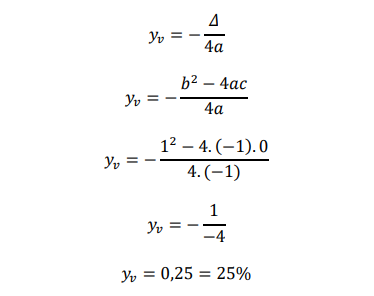
Esse espalhamento máximo de 25% ocorre para percentual de pessoas que conhecem a notícia (x) dado por:
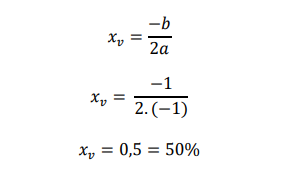
Logo, o espalhamento máximo é de 25%. Nesse caso, não se pode obter um espalhamento superior a 50%. O gabarito, portanto, é ERRADO.
Gabarito: ERRADO.
30. O espalhamento de uma notícia será tanto maior quanto maior for o número de pessoas que dela tiverem tomado conhecimento.
No item anterior, vimos que o espalhamento é uma função do segundo grau com concavidade virada para baixo.
Veja, portanto, que existe um espalhamento máximo que ocorre quando o número de pessoas que tiverem conhecimento da notícia é xv = 50%. Valores de conhecimento maiores do que 50% geram valores de espalhamento menores do que 25%.
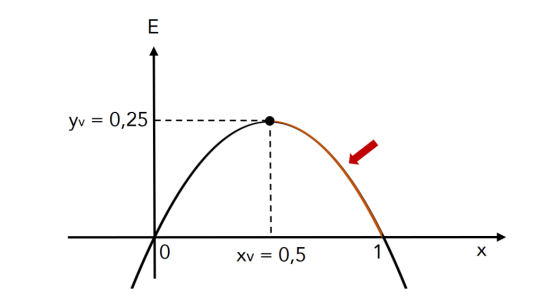
Logo, é ERRADO afirmar que o espalhamento de uma notícia será tanto maior quanto maior for o número de pessoas que dela tiverem tomado conhecimento.
Perceba, ainda, que se 100% das pessoas tomaram conhecimento da notícia, o espalhamento é zero:
E = x. (1 − x)
E = 1. (1 − 1)
E = 1 . 0
E = 0%
Gabarito: ERRADO.
Prof. Francisco Rebouças
Em uma operação da PRF, foram fiscalizados: 20 veículos automotores até o fim da primeira hora; 60 veículos automotores até o fim da segunda hora; 120 veículos automotores até o fim da terceira hora; 200 veículos automotores até o fim da quarta hora; e 300 veículos automotores até fim da quinta hora. O padrão numérico observado manteve-se até o fim da décima hora, quando, então, foi finalizada a operação.
Considerando essa situação hipotética, julgue os itens seguintes.
31. Mais de 550 veículos terão sido fiscalizados até o fim da sétima hora da realização da operação.
Comentários:
Para começar, é interessante organizar as informações do enunciado.
Veículos fiscalizados:
• Até o fim da 1ª hora: 20
• Até o fim da 2ª hora: 60 (40 a mais do que na hora anterior)
• Até o fim da 3ª hora: 120 (60 a mais do que na hora anterior)
• Até o fim da 4ª hora: 200 (80 a mais do que na hora anterior)
• Até o fim da 5ª hora: 300(100 a mais do que na hora anterior)
Observem que a cada hora que passa, 20 veículos são fiscalizados a mais do que na hora anterior. Ao perceber esse padrão, podemos ir além e calcular quantos veículos foram fiscalizados na 6ª e 7ª hora. Como na quinta hora foram fiscalizados 100 veículos, então, na sexta hora serão fiscalizados 120 e na quarta hora, 140.
Veículos fiscalizados:
• Até o fim da 6ª hora: 300 + 120 = 420 (120 a mais do que na hora anterior)
• Até o fim da 7ª hora: 420 + 140 = 560 (140 a mais do que na hora anterior)
Portanto, tivemos 560 veículos fiscalizados até o fim da sétima hora.
Gabarito: CERTO.
Considere que {qn}, para n variando de 1 a 10, seja a sequência numérica formada pelas quantidades de veículos fiscalizados apenas n decorrer da n-ésima hora de realização da operação, ou seja, q1 é a quantidade de veículos fiscalizados apenas no decorrer da primeira hora de realização da operação; q2 é a quantidade de veículos fiscalizados apenas no decorrer da segunda hora de realização da operação; e assim por diante. Nessa situação, a sequência {qn}, para n variando de 1 a 10, é uma progressão aritmética.
Comentários:
A sequência que o enunciado trouxe é formada pelas quantidades de veículos fiscalizados apenas naquela hora específica. Esse “apenas” é muito importante, pois muitos alunos, no calor da prova, podem ter achado que a sequência procurada era {20, 60, 120, 200, 300, … }. Quem pensou que era essa a sequência, acabou errando a questão.
Esse “apenas” restringe a quantidade de veículos que foram efetivamente fiscalizados naquela hora. Por exemplo, na primeira hora, quantos veículos foram fiscalizados? O enunciado disse que foram 20. Logo, q1 = 20. Já na segunda hora, quantos veículos foram fiscalizados? O enunciado disse que até o fim da segunda hora tinham sido 60 veículos.
Atenção aqui! Nós devemos excluir os 20 que tinham sido fiscalizados anteriormente. Assim, obtemos 40 veículos fiscalizados apenas na segunda hora. Todos esses cálculos foram feitos no item anterior, estou apenas detalhando um pouco mais para vocês. Puxando o que já fizemos, a sequência procurada seria:
{20, 40, 60, 80, 100, 120, 140, 160, 180, 200}
Lembre-se que uma progressão aritmética é uma sequência em que a diferença entre dois termos consecutivos será sempre uma constante. Note que a diferença entre quaisquer dois termos consecutivos da sequência acima é 20. Portanto, a sequência {qn} realmente é uma progressão aritmética conforme afirma o item.
Gabarito: CERTO.
Esse é o nosso gabarito extraoficial da disciplina de Raciocínio Lógico Matemático. Esperamos que tenham ido bem na matéria. Até a próxima!
Abraços!