Matemática PM SP (Soldado) – prova resolvida e gabarito
Fala pessoal! Deixo abaixo os enunciados de todas as questões de Matemática da PM/SP, para você que pretende treinar resolvendo essas questões. Na sequência você verá todas as questões resolvidas, ok? A prova foi bem tranquila, padrão VUNESP, sem grandes surpresas para os candidatos bem preparados.
Acredito que meus alunos devem ter obtido um excelente desempenho, pois trabalhamos exaustivamente todos os tópicos do edital ao longo das aulas!
VUNESP – PM/SP – 2017) A tabela mostra a movimentação da conta corrente de uma pessoa em determinado dia.
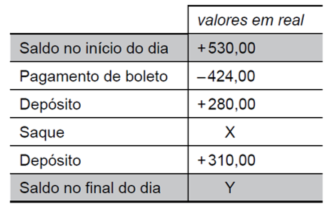
Sabendo-se que o saldo, no final do dia, era positivo e correspondia a 20% do valor do saldo do início do dia, então o valor de X, em reais, é
(A) – 410,00.
(B) – 530,00.
(C) – 590,00.
(D) – 620,00.
(E) – 480,00.
VUNESP – PM/SP – 2017) Um carro parte da cidade A em direção à cidade B e, após percorrer 1/8 da distância entre as duas cidades, passa pelo 1º pedágio. Percorre mais 1/5 da distância entre as duas cidades e passa pelo 2o pedágio. Se a distância entre o 2º pedágio e a cidade B é de 459 km, então a distância percorrida entre a cidade A e o 1º pedágio, em km, é
(A) 85.
(B) 125.
(C) 115.
(D) 95.
(E) 105.
VUNESP – PM/SP – 2017) Um escritório comprou uma caixa de envelopes e irá dividi-los em pequenos pacotes, cada um deles com o mesmo número de envelopes. Se em cada pacote forem colocados ou 8 envelopes, ou 9 envelopes, ou 12 envelopes, não restará envelope algum na caixa. Sabendo-se que, nessa caixa, há menos de 400 envelopes, então o número máximo de envelopes dessa caixa é
(A) 256.
(B) 288.
(C) 342.
(D) 360.
(E) 385.
VUNESP – PM/SP – 2017) Em um armário, a razão entre o número de gavetas vazias e o número de gavetas ocupadas é 1/9. Após se esvaziarem duas gavetas que estavam ocupadas, a razão entre o número de gavetas vazias e o número de gavetas ocupadas passou a ser 1/5. Sendo assim, o número de gavetas ocupadas nesse armário passou a ser
(A) 19.
(B) 25.
(C) 16.
(D) 21.
(E) 28.
VUNESP – PM/SP – 2017) Em uma caixa, havia 150 peças, das quais 30% estavam enferrujadas e, portanto, não podiam ser utilizadas. Das demais peças, 20% apresentavam defeitos e também não podiam ser utilizadas. Considerando-se o número total de peças da caixa, é correto dizer que o número de peças que podiam ser utilizadas representava
(A) 52%.
(B) 44%.
(C) 40%.
(D) 48%.
(E) 56%.
VUNESP – PM/SP – 2017) Para percorrer um determinado trecho de estrada, um carro com velocidade constante de 80 km/h gasta 45 minutos. Se esse carro percorresse esse mesmo trecho com velocidade constante de 100 km/h, gastaria
Dado: quilômetros por hora (km/h) expressa o número de quilômetros percorridos em uma hora
(A) 36 minutos.
(B) 32 minutos.
(C) 42 minutos.
(D) 30 minutos.
(E) 39 minutos.
VUNESP – PM/SP – 2017) A média aritmética das idades dos cinco jogadores titulares de um time de basquete é 22 anos. Um dos jogadores titulares desse time, que tem 20 anos de idade, sofreu uma lesão e foi substituído por outro jogador, o que fez com que a nova média das idades dos cinco jogadores do time titular passasse a ser de 23 anos. Então, a idade do jogador que substituiu o jogador lesionado é
(A) 23 anos.
(B) 21 anos.
(C) 25 anos.
(D) 24 anos.
(E) 22 anos.
Observação: sobre essa última questão, veja como é importante treinar com questões anteriores. As duas questões abaixo (que estavam em nosso curso) são praticamente iguais:
VUNESP – PROCON/SP – 2013) A média das idades dos 5 funcionários de uma loja era 35 anos. Sabendo que o funcionário que tinha 68 anos de idade se aposentou e que foi contratado em seu lugar uma pessoa com 25 anos de idade, pode-se afirmar que a nova média das idades desses funcionários, em anos, passou a ser de…
VUNESP – PREF. SJC – 2012) A média aritmética de alturas de 10 alunos de um time de futebol é 175 cm. Dois novos alunos entram para o time, e a nova média de alturas passa a ser 178 cm. Se a diferença entre as alturas desses dois novos jogadores é 6 cm, o maior dos dois mede, em cm…
VUNESP – PM/SP – 2017) Uma loja tem uma caixa cheia de tapetes e irá formar com eles pilhas, cada uma delas com o mesmo número de tapetes. Se forem colocados 12 tapetes em cada pilha, não restará tapete algum na caixa; e, se forem colocados 15 tapetes em cada pilha, serão feitas 2 pilhas a menos, e também não restará tapete algum na caixa. Assim, o número de tapetes que há na caixa é
(A) 210.
(B) 120.
(C) 150.
(D) 90.
(E) 180.
VUNESP – PM/SP – 2017) Uma pessoa comprou empadas e coxinhas, num total de 30 unidades, e pagou R$ 114,00. Sabendo-se que o preço de uma empada é R$ 3,50 e o preço de uma coxinha é R$ 4,00, então o número de coxinhas compradas foi
(A) 12.
(B) 18.
(C) 20.
(D) 14.
(E) 16.
VUNESP – PM/SP – 2017) A tabela mostra o tempo de cada uma das 4 viagens feitas por um ônibus em certo dia.
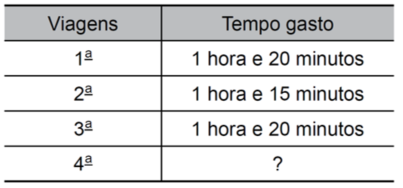 Se o tempo total gasto nas 4 viagens juntas foi de 5 horas e 25 minutos, então o tempo gasto na 4a viagem foi de
Se o tempo total gasto nas 4 viagens juntas foi de 5 horas e 25 minutos, então o tempo gasto na 4a viagem foi de
(A) 1 hora e 25 minutos.
(B) 1 hora e 20 minutos.
(C) 1 hora e 15 minutos.
(D) 1 hora e 30 minutos.
(E) 1 hora e 10 minutos.
VUNESP – PM/SP – 2017) Para uma reunião, foram preparados 5 litros de café.
Após o consumo de 75% desse café, o restante foi dividido igualmente em 2 garrafas térmicas. Assim, a quantidade de café, em mL, contida em uma garrafa térmica era de
(A) 625.
(B) 675.
(C) 600.
(D) 650.
(E) 575.
VUNESP – PM/SP – 2017) A figura mostra duas salas, A e B, ambas retangulares, com medidas em metros.
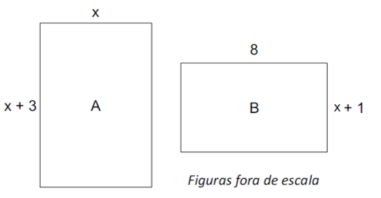
Sabendo-se que as duas salas têm o mesmo perímetro, pode-se afirmar que a área da sala A, em m2, é
(A) 54.
(B) 48.
(C) 52.
(D) 50.
(E) 56.
Agora está certinho :) eu havia trocado as coxinhas com as empadas rs
Abraço
Oi Ana, infelizmente eu entendo que não.
Abraço