Questão Interessante – CESPE – Polícia Federal 2018
Fala, pessoal!
Neste artigo, vou resolver uma questão muito interessante do CESPE, que caiu na prova para Papiloscopista da Polícia Federal em 2018.
Sabemos que o conectivo “se…, então…” é um dos mais recorrentes em provas de concursos e, muitas vezes, ele aparece camuflado com outras expressões da língua portuguesa.
Foi justamente uma dessas “camuflagens” que derrubou muitos candidatos na questão do concurso da Polícia Federal.
Algumas “camuflagens” da condicional são bem conhecidas. Veja alguns exemplos:
- “Sempre que vou ao shopping, faço compras” é o mesmo que “Se vou ao shopping, então faço compras”.
- “Penso, logo existo” é o mesmo que que “Se penso, então existo”.
- “Quando vou à praia, bebo” é o mesmo que “Se vou à praia, então bebo”.
- “Bebo somente se vou à praia” é o mesmo que “Se bebo, então vou à praia”.
- “Todo recifense é pernambucano” é o mesmo que “Se uma pessoa é recifense, então ela é pernambucana”.
- “A, pois B” é o mesmo que “Se B, então A”.
Pois bem, qual a interpretação correta de uma frase como “Vou à praia, a menos que chova” ou “Vou à praia, a não ser que chova”.
Pois bem, tais proposições equivalem a “Se não chover, então vou à praia”.
De uma maneira geral, uma proposição do tipo “P, a não ser Q” ou “P, a menos que Q” pode ser traduzida simbolicamente como “~Q —> P”, ou seja, “Se não Q, então P”.
Esse caso pode ser encontrado, por exemplo, no livro “Boolean Algebra and its applications” do autor J. Eldon Whitesitt. Observe a linha do “p unless q” no referido livro.
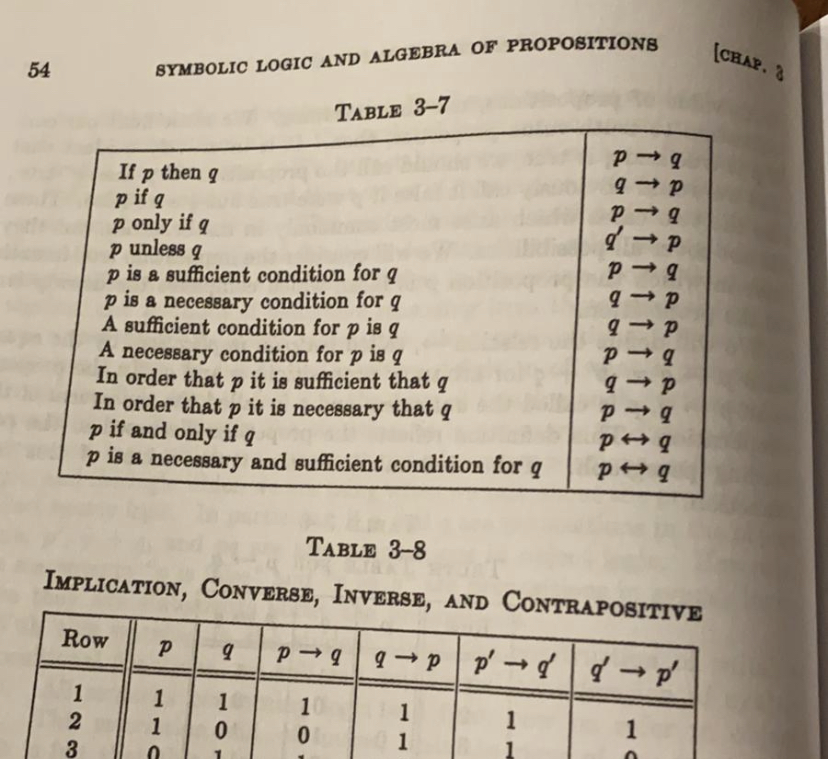
Vamos agora resolver a questão do concurso da Polícia Federal?
(CESPE 2018/Polícia Federal – Papiloscopista)
Julgue o item, acerca da seguinte proposição:
P: “A nomeação do novo servidor público ocorre para reposição de vacância em área essencial, ou o candidato aprovado não será nomeado”.
A proposição P é logicamente equivalente à proposição: “Não é verdade que o candidato aprovado será nomeado, a não ser que a nomeação do novo servidor público ocorra para reposição de vacância em área essencial”.
Vamos utilizar símbolos para as proposições simples envolvidas.
A: A nomeação do novo servidor público ocorre para reposição de vacância em área essencial.
B: O candidato aprovado será nomeado.
A proposição P pode ser representada por “A ou ~B”.
Vamos agora analisar a outra proposição dada no enunciado: “Não é verdade que o candidato aprovado será nomeado, a não ser que a nomeação do novo servidor público ocorra para reposição de vacância em área essencial”
Essa proposição pode ser simbolicamente representada por “~B, a não ser que A”.
Vimos anteriormente que uma proposição do tipo “P, a não ser Q” corresponde a “Se ~Q, então P”.
Logo, a proposição “ ~B, a não ser que A” corresponde ao condicional “Se ~A, então ~B”.
Vamos agora relembrar que toda proposição composta pelo conectivo “se…, então…” pode ser reescrita como uma proposição composta pelo conectivo “ou”). Para tanto, devemos negar o antecedente e manter o consequente. Essa é uma importante e famosa equivalência lógica.
Assim, a proposição “Se ~A, então ~B” equivale à proposição “A ou ~B”, que, por sua vez, é a própria proposição P.
O item está certo.
Abraços,
Guilherme Neves