Caro aluno,
Neste artigo vamos conversar sobre a negação de dois tipos de proposições lógicas muito cobradas em provas de concurso, e que geram muitas dúvidas nos candidatos. Trata-se daquelas contendo as expressões “todo” ou “nenhum”.
Para começar, você se lembra o que é o conceito de negação de uma proposição? Guarde bem isso: a negação de uma proposição p é uma outra proposição cujo valor lógico é SEMPRE oposto ao da proposição original. Viu que eu destaquei o “sempre”? Isto será fundamental para o entendimento do tema de hoje…
Veja agora a seguinte proposição lógica:
“Todo coelho é verde”
Para encontrar a negação desta proposição, use o seguinte “macete”:
Portanto, admitindo que alguém te fez a afirmação de que “Todo coelho é verde”, o que é o mínimo que você precisa fazer para provar que isto é mentira? Você precisa analisar TODOS os coelhos do mundo para verificar que nenhum deles é verde e então dizer que “Nenhum coelho é verde”? Ou basta que você encontre um coelho que não seja verde para demonstrar que a afirmação é mentirosa? Neste caso, basta encontrar um coelho que não seja verde, afinal o autor da frase está afirmando que TODO coelho é verde. Por isto, a negação é dada pela frase:
“Pelo menos um coelho NÃO é verde”
ou então:
“Algum coelho NÃO é verde”
ou então:
“Existe coelho que NÃO é verde”
E assim por diante, existem várias variações desta frase. Agora vamos buscar a negação da seguinte frase:
“Nenhum coelho é verde”
Vamos imaginar que alguém nos afirmou isso. O que é o MÍNIMO que precisamos fazer para desmentir esta pessoa? Precisamos verificar se TODOS os coelhos do mundo são verdes? Ou basta encontrarmos algum coelho que seja verde? Repare que o mero fato de encontrarmos algum coelho que realmente seja verde já é suficiente para mostrar que a frase é mentirosa, afinal ela afirma que NENHUM coelho é verde. Por isso, a sua negação é dada por:
“Algum coelho é verde”
“Pelo menos um coelho é verde”
“Existe coelho verde”
E assim por diante…
Agora vem a pergunta que MUITOS, MUITOS alunos mesmo me fazem: professor, por quê não posso negar “Todo coelho é verde” dizendo que “Nenhum coelho é verde”? Essas frases não possuem valores opostos?
De fato essas frases transmitem ideias relativamente antagônicas. Mas elas NÃO são negação uma da outra, no sentido da lógica de proposições, lógica formal ou lógica dedutiva. Você pode verificar lembrando do conceito básico de negações: para uma proposição ser negação da outra, elas devem ter valores lógicos opostos SEMPRE! Se uma é verdadeira, a outra necessariamente deve ser falsa, e vice-versa. Não pode ocorrer de ambas serem verdadeiras ou ambas serem falsas ao mesmo tempo!
Aí eu te pergunto: o que aconteceria se os biólogos descobrissem que existem algumas espécies de coelhos que são verdes e outras espécies que não são verdes? Neste caso, tanto a frase “Todo coelho é verde” como a frase “Nenhum coelho é verde” seriam FALSAS, concorda? Afinal existiriam coelhos verdes e não-verdes… ou seja, neste caso seria possível que as DUAS proposições tivessem o MESMO valor lógico (F), o que é inadmissível em se tratando de negações lógicas. É por este motivo que TODO não é a negação de NENHUM, e vice-versa!
Prosseguindo, imagine agora a frase:
“Algum coelho é verde”
Como encontramos a negação dela? Basta imaginar que alguém nos disse isso e buscar o mínimo que precisamos fazer para desmentir esta pessoa. Neste caso, como a pessoa disse que algum coelho é verde (e não todos os coelhos), não adianta simplesmente encontrarmos um contra-exemplo (um coelho que não seja verde). Precisamos verificar TODOS os coelhos do mundo e confirmar que, realmente, nenhum deles é verde. Por isso, a negação desta frase é:
“Nenhum coelho é verde”
ou
“Todo coelho NÃO é verde”
ou
“Não existe coelho verde”
Para terminar, vamos encontrar a negação de:
“Algum coelho não é verde”
Se alguém nos disser isso, precisamos fazer o que para desmentir esta pessoa? Como está sendo afirmado que algum coelho não é verde, precisamos avaliar todos os coelhos e demonstrar que todos eles realmente são da cor verde. Não basta encontrarmos um ou dois coelhos que sejam verdes, ou mesmo um milhão de coelhos verdes, pois se houver por aí algum coelho que seja de outra cor (branco, por exemplo), a frase da pessoa estará correta. Por isso, a negação é dada por:
“Todo coelho é verde”
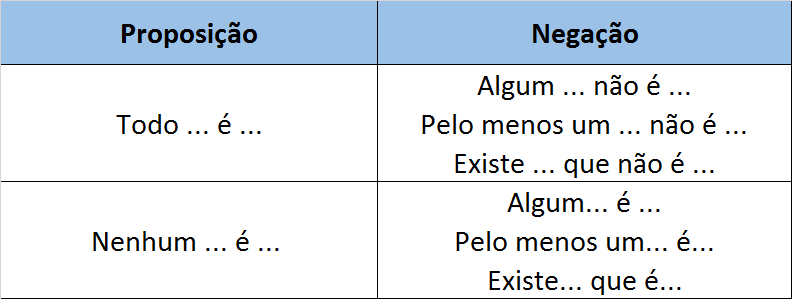
Ficou claro? Espero que sim. Deixo abaixo uma tabelinha com um resumo bem legal para você – embora eu NÃO aconselhe você a decorar, mas sim a ENTENDER a lógica da nossa análise.
E não deixe de conhecer os meus CURSOS EM ANDAMENTO, clicando AQUI. Espero poder ajudá-lo a conseguir aquela tão sonhada aprovação!
Saudações,
Prof. Guilherme Neves