Ângulos, arcos e cordas na circunferência
Olá, pessoal! Hoje falaremos sobre os ângulos, arcos e cordas na circunferência. Esse tema é bastante comum em geometria plana e muito cobrado em concursos e vestibulares, notadamente para carreiras militares. Abordaremos também algumas definições e fórmulas importantes que se relacionam a essa matéria. Alertamos, apenas, que os aspectos serão tratados de maneira bem objetiva visando marcar o X no lugar certo.
Conceitos de ângulos, arcos e cordas.
Inicialmente, não podemos fugir dos conceitos.
Ângulo, em geometria plana, é a União de 2 (dois) segmentos de reta a partir de um ponto comum. O Ângulo está presente em qualquer forma geométrica (triângulo, círculo, quadrado etc.). Na circunferência, o ângulo pode ser assim representado:
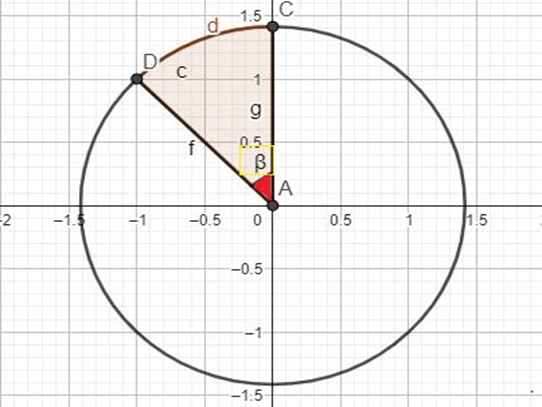
Nessa imagem, podemos definir, por oportuno, o raio da circunferência que é a distância que une o centro à borda. No caso, o raio é tanto AD quando AC.
Já o arco(DC) é a projeção que essas semirretas têm na borda da circunferência. Ou mais facilmente, é uma parte da circunferência determinada por 2(dois) pontos distintos.
No caso da imagem acima, β seria o ângulo (destacado em vermelho) e DC seria o arco. A região sombreada é chamada de Setor Circular.
A corda, nobres, é a união de 2(dois) pontos na circunferência através de um segmento de reta. Vejamos sua representação:
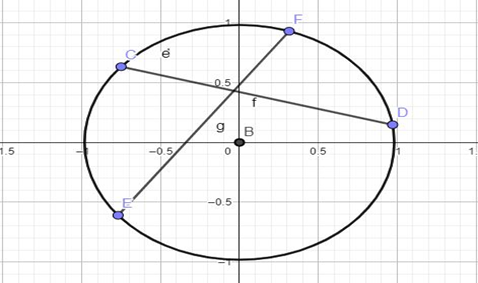
São cordas os seguimentos CD e EF.
Aplicações com ângulos, arcos e cordas na circunferência
Passados os conceitos iniciais, vamos analisar algumas situações práticas envolvendo ângulos e arcos.
De início, pessoal, todos devem ter em mente que a circunferência possui um total de 360º, certo?!. Visando facilitar a representação matemática, criou-se o radiano (π), que é a razão entre o comprimento de um arco e seu raio. A partir da conversão de ângulos, tem-se que π = 180º. Assim, qualquer ângulo pode ser escrito em radiano. Logo, não se assuste se aparecer esse símbolo na sua prova. Vamos para mais alguns exemplos:
2π = 360º; 3π/2 = 270º e assim, sucessivamente.
Pois bem, vamos a algumas situações especificas.
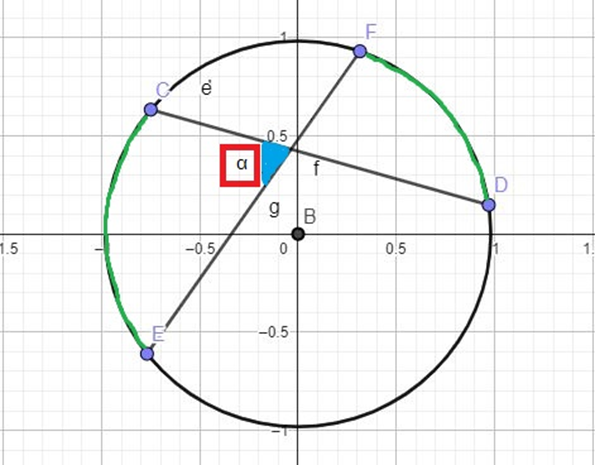
Como saber o tamanho do arco ou do ângulo em graus? Nesse caso, vale a seguinte relação: α= β/2 ou α = DC/2.
Assim, por definição, o ângulo α mede β/2, da mesma forma, α vale o tamanho do arco DC/2. Se por exemplo, α = 30º, β = 60º e o arco DC=60º. Como falamos, nobres, isso pode ser demonstrado matematicamente, mas não o faremos aqui. Porém, vejam que o ângulo β se localiza no centro da circunferência e isso facilita demais os cálculos.
Vejamos, entretanto, se o Ângulo for excêntrico interno ou externo.
Como representação do ângulo excêntrico interno:
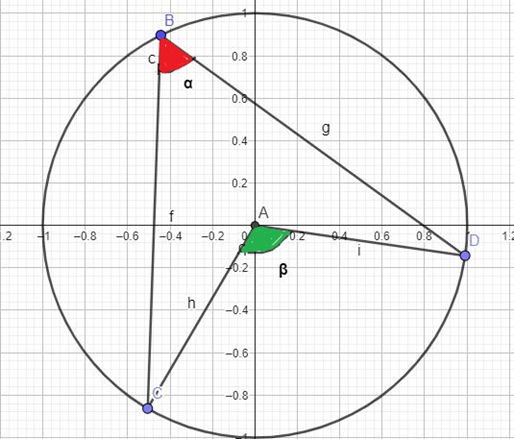
Nesse caso, por definição, o valor de α será o comprimento dos dois arcos divididos por 2. Ou seja, α = (EC + FD)/2.
Se o Ângulo for excêntrico externo:
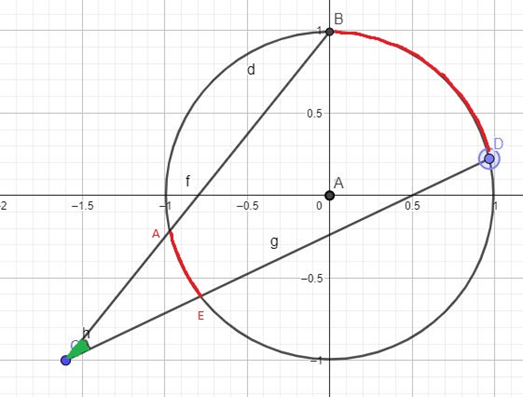
O valor do ângulo C(em verde) é a diferença do tamanho dos arcos, ou seja: C = (DB – AE)/2
Relações importantes com as Cordas
Com o conceito de “Cordas” temos uma importante relação que pode ajudar muito na resolução de questões. É a chamada Potência de Ponto interior.
Quando duas cordas se cruzam(no ponto P), geram-se 4 semirretas em que temos a seguintes forma e definição:
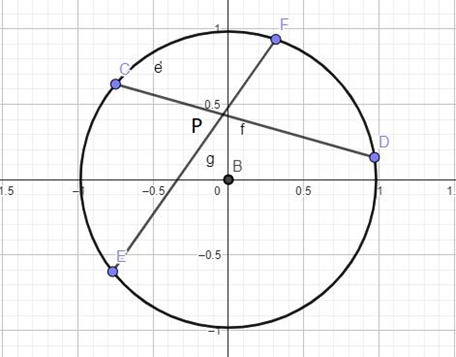
No caso, tem-se que PC*PD = PF*PE
Aplicação dos conhecimentos na circunferência
Questão nº 01
Vamos aplicar os conhecimentos sobre Ângulos, arcos e cordas na circunferência numa questão do Instituto Tecnológico da Aeronáutica:
(ITA – 2006 – 1ª fase)
Seja E um ponto externo a uma circunferência. Os segmentos EA e ED interceptam essa circunferência nos pontos B e A, e, C e D, respectivamente. A corda AF da circunferência intercepta o segmento ED no ponto G. Se EB = 5, BA = 7, EC = 4, GD = 3 e AG = 6, então GF vale:
Resolução: De início, é sempre bom representar a questão por meio do desenho.
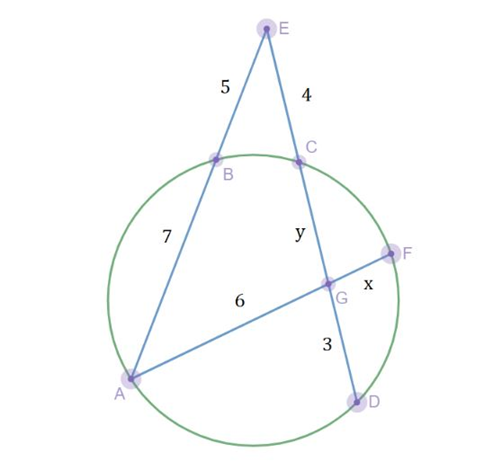
Inicia-se com a Potência de Ponto externa E.
EB*EA = EC*ED
5*12 = 4*(GC + 7), Logo, GC = 8
Após, aplica-se a potencia de ponto interna:
GA.GF = GC.GD
6*GF = 8*3
GF = 4 (gabarito)
Questão nº 02
Mais uma questão, agora cobrada na prova de admissão à Escola Naval em 2004
O quadrilátero MNPQ está inscrito em uma circunferência de centro O e raio 6cm, conforme a figura acima. Sabe-se que QM =3cm, MN =8cm e que a diagonal MP passa por O . Se E é um segmento QN, tal que ME é perpendicular a QN. Então o valor do perímetro do triângulo QME, em cm, é:
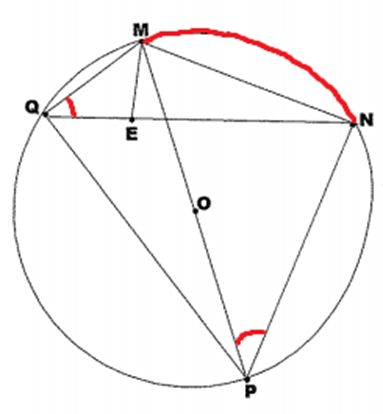
Resolução; Pessoal, vejam que o arco referente ao ângulo Q do triângulo MQN é igual ao arco do ângulo P do triângulo MPN. Assim, o triângulo MQE e o triângulo MPN são semelhantes, de modo que eles guardam relação de proporcionalidade entre seus lados. Assim, temos:
ME/MN = QM/MP
Obs. Na semelhança de triângulos, seguimos a mesma ordem, ou seja, lado oposto ao ângulo de um triangulo, dividido pelo lado oposto do ângulo do outro triangulo. E assim por diante…
ME/8 =3/12,
Logo ME = 2
Para encontrarmos o outro lado do triângulo MQE é só aplicar o teorema de Pitágoras, pois o comando da questão citou que ME é perpendicular a QN. Logo, forma-se um ângulo de 90º.
Desta forma, 32 = 22+ QE2
QE = √5
O Perímetro (soma dos lados do triângulo) = 2 + 3 + √5
Perímetro = 5 + √5
Percebemos que essa última questão explorou outros conhecimentos além da semelhança dos triângulos pelos arcos iguais.
Conclusão
É isso, pessoal! Apresentamos alguns conceitos iniciais sobre ângulos, arcos e cordas na circunferência. Os conhecimentos acima são base para diversos outros que envolvem circunferência. Aos poucos, vamos trazendo conteúdos mais avançados a fim de que auxiliem a todos na aprovação que tanto desejam.
Bons Estudos.