Fala, pessoal! Hoje iremos falar sobre as transformações trigonométricas, notadamente o Seno, o Cosseno e a Tangente. Essas transformações nos auxiliam, e muito, na resolução de questões. Ademais, esse tipo de conhecimento se torna mais importante em vestibulares e em concursos de admissão às Forças Armadas(Exército, Marinha e Aeronáutica).
Inicialmente, o seno, o cosseno e a tangente representam importantes funções no mundo da matemática, principalmente no campo da trigonometria. Essas relações nos auxiliam, a partir de um dado ângulo, a encontrarmos valores e comportamentos de determinadas variáveis. Todavia, o seno, cosseno e tangente apresentam diferentes visões quando aplicados em um triângulo retângulo ou quando aplicados no círculo trigonométrico.
No triângulo, o seno de um ângulo qualquer X equivale ao cateto(lado) oposto ao ângulo em referência dividido pela hipotenusa(cujo ângulo correspondente é o de 90º). Logo, Sen X = Cateto oposto/Hipotenusa.
Por sua vez, o cosseno equivale ao cateto(lado) adjacente ao ângulo em referência dividido pela hipotenusa. Logo, Cos X = Cateto adjacente/Hipotenusa.
Por fim, a tangente(Tg) de um ângulo X é o cateto oposto dividido pelo cateto adjacente. Ou, noutras palavras, Tg X = Sen X/ Cos X.
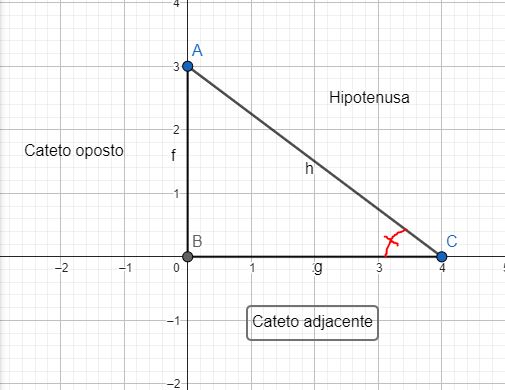
Obs. Na imagem acima considerem que o ângulo X corresponde ponto C do triângulo.
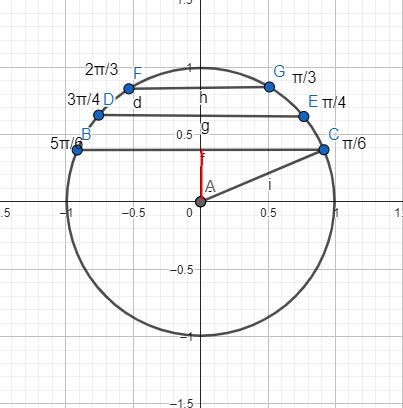
Vejam que aqui temos uma função sen x. Cada valor de X, com a sua imagem no círculo(pontos B,C, D, E, F e G) possui um correspondente na reta vertical(eixo das ordenadas grifado em vermelho). Nobres, não custa lembrar que símbolo(π) corresponde ao valor de 180º.
Assim, na imagem acima, vemos que quando o X vale (π)/6 ou 30º, o seu seno é 0,5 ou 1/2.
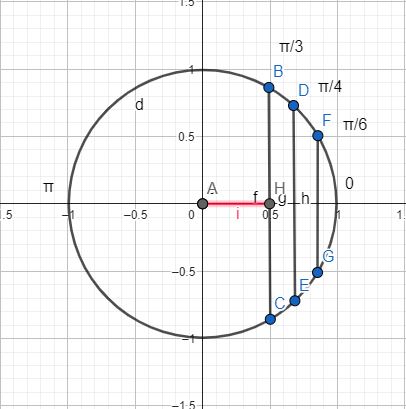
A função cosseno tem a estrutura bem parecida com a função seno. Ocorre que o correspondente ao ângulo no círculo tem seu equivalente no eixo das abcissas(eixo horizontal).
Por conseguinte, veja na imagem que o cosseno de (π)/3 ou 60º é justamente 0,5 ou 1/2.
Notadamente, essas transformações trigonométricas têm por objetivo prático transformar ângulos cujo seno, cosseno e tangente são desconhecidos em ângulos notáveis(30º, 45º, 60º), que possuem valores bem conhecidos.
Passados esse conceitos iniciais, vamos às transformações trigonométricas mais famosas.
Antes, porém, vamos considerar que: Sen = Seno, Cos = Cosseno e Tg = Tangente, ok?!
A primeira fórmula é a da adição:
Cos (a + b) = Cos a. cos b – Sen a . Sen b.
Ex. Qual o cosseno de 75º?
Cos(75º) = Cos (45º + 30º) = Cos 45º . Cos 30º – Sen 45º . Sen 30º
Assim, temos: √2/2. √3/2 – √2/2 . 1/2, Logo, Cos 75º = (√6 – √2)/4
Com a função seno, temos:
Sen(a + b) = Sena . Cos b + Sen b . Cos a
Ex. Qual o seno de 105º?
Sen 105º = Sen (60º + 45º)
Logo, Sen (60º + 45º)= Sen 60º . Cos 45º + Sen 45º . Cos 60º.
Isso perfaz (√6 + √2)/4.
Do mesmo modo, podemos transformar ângulos a partir de operação de subtração.
Da função cosseno, temos:
Cos (a – b) = Cos a. Cos b + Sen a . Sen b
Da função seno, temos:
Sen(a – b) = Sen a . Cos b – Sen b . Cos a
Pessoal, só a título de complementação do conhecimento, vamos apresentar as transformações trigonométricas da função tangente também.
Na adição, temos:
tg(a + b) = (tg a + tg b)/(1 – tg a . tg b)
Na subtração, por sua vez:
tg(a – b) = (tg a – tg b)/(1 + tg a . tg b)
Vejam que o que difere a adição da subtração em TODAS as transformações são os jogos de sinais (mais e menos). Então, muita atenção!
Ex. Tangente de 75º
tg 75º = tg(45º + 30º)
tg(45º + 30º) = (1 + √3/3)/ (1 – 1.√3/3)
tg 75º = 2 + √3.
Para finalizar, vamos comentar uma questão bem interessante que caiu no concurso da Controladoria Geral da União – Cargo de Técnico – aplicada pela FGV(Fundação Getúlio Vargas) em 2022:
Um avião percorria a trajetória reta XY da figura abaixo, de X para Y, quando o piloto percebeu turbulências à frente. Para evitá-las fez, no ponto A, um giro na trajetória para a esquerda e percorreu 10 km. No ponto B fez um giro de 53o para a direita e, ao percorrer mais 10 km, percebeu que tinha atingido o ponto C da trajetória inicial.
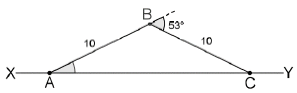
Dados:
Use o necessário,
sen37°=0,6
cos37°=0,8 e √5 = 2,24
A distância entre os pontos A e C é, aproximadamente?
Caros concurseiros, essa questão apresenta um bom nível de cobrança e aborda diversos temas.
Primeiramente veja que se o ângulo externo mede 53º, o ângulo interno ao triângulo mede 127º(180º – 53º).
Então, para descobrirmos a distância de A até C, podemos aplicar a lei dos cossenos nesse triângulo! Nobres, já detalhamos essa LEI dos Cossenos em artigo anterior (Nobres, perdoe-me pela gafe, mas nesse artigo eu citei/inverti incorretamente os valores do seno e cosseno de 90º, bem como o de180º- Assim, o correto seno de 90º é 1 e o cosseno de 90º é 0. Já o seno de 180º é 0 e o cosseno é -1).
Vamos chamar a distância AC de X.
Logo, X2= 102 + 102−2.10.10.cos127º.
Porém aqui temos um problema: Como saber o Cosseno de 127º??
Para isso, vamos usar o conhecimento adquirido aqui acerca de transformações trigonométricas. Veja que 127º = 90º + 37º. Olhem que a questão forneceu o Sen 37º(Bingo!!!).
Vamos aplicar a transformação do Cosseno:
Cos 127º = Cos (90º + 37º) = Cos 90º . Cos 37º – Sen 37º . Sen 90º
Sabe-se que 90º é um ângulo notável que possui Cosseno = 0 e seno = 1
Assim, Cos(90º + 37º) = 0 . Cos 37º – 0,6 . 1
Cos(90º + 37º) = – 0,6
Aí, é só “correr para o abraço”.
X2= 102 + 102−2.10.10.cos127º:
X2= 102 + 102−2.10.10.(-0,6)
X2 = 320
X = √320, que fatorando vale: 8√5
Como foi dado na questão que √5 = 2,24, temos que a distância AC = 8.2,24 = 17,92km(GABARITO).
Então é isso, nobres. Chegamos ao fim de mais um artigo que abordou, desta vez, as transformações trigonométricas e o quão são importantes para a resolução de questões. Fizemos questão de mostrar em detalhes as funções do seno e cosseno pois são, de longe, as mais cobradas. Esperamos que tenha sido de grande valia.
Bons Estudos!