Propriedades dos triângulos
Olá, pessoal. Vamos abordar algumas fórmulas e propriedades dos triângulos em diferentes contextos. Esse conteúdo pode ser importante para você que está se preparando para concursos militares e para alguns concursos da área fiscal que cobram figuras geométricas. Lembrando que serão temas mais avançados(fugiremos do básico).
Cálculo a partir das propriedades dos triângulos
Nobres, aqui não iremos tratar da “velha” fórmula para área do triângulo(base x altura/2). Iremos abordar temáticas mais complexas para ser um diferencial em sua preparação.
Pessoal, a depender dos dados que a questão forneça, há fórmulas muito importantes. E saber qual fórmula usar exige conhecimento dos dados fornecidos para que se “ganhe” tempo na hora da prova. Vamos juntos!
Lei(fórmula) dos senos
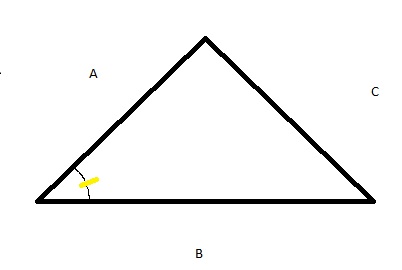
A primeira fórmula é: (a.b.Sên.C)/2 – Nessa você precisaria ter ao menos 2 lados(A e B) conhecidos e saber o seno do ângulo referente ao terceiro lado(C – grifado em amarelo).
Aplicando os conhecimentos: Vamos supor que no triângulo acima a=5, b=8, c=7 e que o ângulo relativo a “C” seja 60°. Pela primeira fórmula teríamos: S = (5.8.Sên C)/2. Logo:
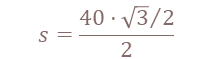
Logo, a área(S) seria:
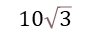
Área do triângulo quando conhecemos apenas os lados
A segunda fórmula, também é muito importante, pessoal. Ela aplica conceitos da lei dos cossenos que traremos abaixo e nos ajuda quando só sabemos os lados do triângulo. Por conseguinte, não sabemos ângulos e quando sabemos, não são aqueles notáveis(que são mais comuns). Falando nisso, é imprescindível que vocês saibam a tabela abaixo:
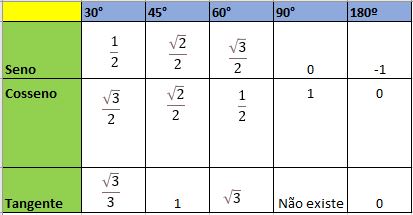
Voltando….
A fórmula é atribuída ao matemático grego Herão de Alexandria e se dá por:
Em legenda:
- A = área;
- p = semiperímetro(que é o perímetro dividido por 2);
- a, b e c são os lados do triângulo.
Da mesma forma, Vamos supor que temos um triângulo de lados a=5, b=8, c=7. Aqui, o semiperímetro seria p=(5 + 8 + 7)/2; p = 10.
Aplicando o teorema de herão temos:

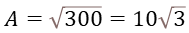
Vejam que ambas as formas(lei dos senos e herão) obtivemos o mesmo resultado.
Lei(fórmula) dos Cossenos
A lei dos cossenos é muito usada para se encontrar lados e/ou ângulos desconhecidos em um triângulo qualquer.
Nobres, a lei dos cossenos é esta:

Por essa fórmula, suponhamos que quiséssemos encontrar o valor do ângulo C, com os dados do nosso triângulo modelo dado no início do artigo.
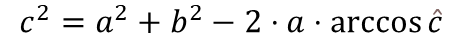
Substituindo os valores: 7^2 = 5^2 + 8^2 – 2.5.8.Cos.C
Ao resolvermos essa equação, encontraríamos Cos.C = 1/2. E qual ângulo que o cosseno é 1/2? Isso mesmo, o ângulo de 60°.
Área do triângulo com circunferência inscrita e circunscrita
Outros casos bem interessantes com triângulos é quando os mesmos possuem circunferências inscritas(dentro) ou circunscritas(fora). Comecemos com a circunferência inscrita:
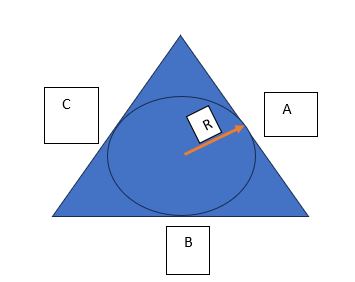
Na figura acima temos os lados do triângulo como A,B e C e R seria o raio da circunferência. Pessoal, por definição, toda reta que sai do centro da circunferência e toca no lado do triângulo (como a reta em laranja da imagem) forma um ângulo de 90º. Como forma-se um ângulo de noventa graus, essa reta do centro ao lado do triângulo é a altura de um triângulo menor. Veja a figura abaixo:
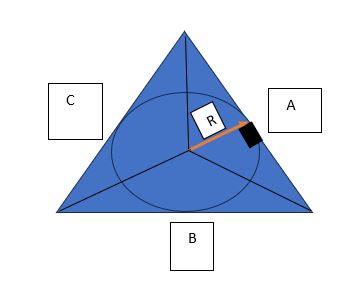
Aí, pessoal, é só aplicar a fórmula básica da área do triângulo(base x altura/2) que você “matará” a questão. Como sugestão de treino, deixamos a questão que caiu na prova da Escola de Sargentos das Armas(ESsA -2014):
Qual é a área da circunferência inscrita num triângulo ABC cuja a área desse triângulo vale 12x(5) 1/2 (doze raiz quadrada de 5) e cujas medidas dos lados, em metros, são 7, 8 e 9:
Comentários: Pessoal, como sabemos a área total, é só dividir o triângulo maior em três menores como fizemos na figura acima. Assim, os lados serão as bases de cada triângulo e o raio(R) as respectivas alturas. Após, só igualar à área total já fornecida.

Logo, R = (5) 1/2 (raiz quadrada de 5) . Por consequência, a área do círculo seria:
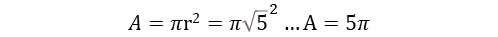
Por sua vez, com a circunferência circunscrita, ou seja, com o triângulo dentro da circunferência, temos a seguinte notação:
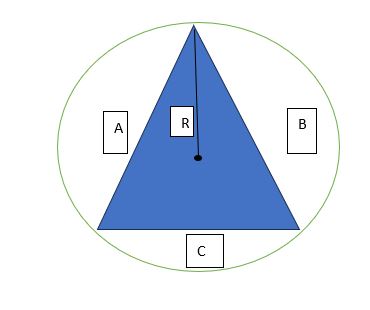
Nobres, aqui a fórmula da área do triângulo é: S = A.B.C/4R. Essa fórmula decorre da 1ª fórmula que estudamos sobre propriedades dos triângulos, qual seja, a lei dos senos. Então, combina-se a lei dos senos com outra relação muito importante que é: Seno(ângulo relativo ao lado B) = B/2R. Lembrando que você pode fazer adaptações, pessoal. Se quiser saber o Seno do lado A ou C, é só alterar os valores.
Conclusão
Então é isso, nobres. Encerramos aqui mais um artigo que tratou de importantes relações trigonométricas e propriedades dos triângulos. Por fim, saibam que são temas um pouco mais avançados, mas que poderão ser o seu diferencial na aprovação.
Bons estudos.
