Olá, nobres! Iremos abordar um tema bem específico da Microeconomia que é: Como calcular a cesta ótima. Este assunto sempre aparece nos editais em que conste a matéria Economia e causa calafrios só de olhar. Vamos entender de uma vez por todas como fazer os cálculos e garantir mais um pontinho rumo à aprovação.
Pessoal, a cesta ótima se encontra na Teoria do Consumidor(matéria estudada em Microeconomia). Na cesta ótima, o consumidor terá 2(dois) itens, suponhamos “X” e “Y”, e , com base em seu orçamento(representado por uma reta) e em suas preferências, preferirá uma certa quantidade de “X” e uma certa quantidade de “Y” que lhe dará mais bem estar.
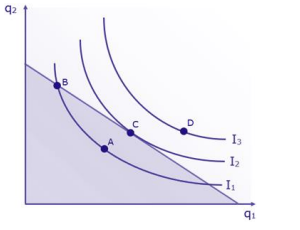
Antes de adentrarmos ao cálculo da cesta ótima, vamos apenas fazer uma breve explanação sobre o gráfico acima. Os pontos A e B estão na mesma curva, chamada de curva de indiferença. Assim, a teoria diz que para o consumidor é INDIFERENTE estar no ponto A ou ponto B, ok?
Mas no campo das preferências, o consumidor preferirá estar no ponto C, em lugar do ponto A. Mas por quê? Por entrar em campo o conceito da UTILIDADE. Ademais, o ponto C gera mais UTILIDADE do que o ponto A e B, por exemplo, pois há maior quantidade de ambos os itens(q1 e q2).
Finalmente, o PONTO C é chamado de equilíbrio do consumidor, pois é o ponto em que a curva de indiferença coincide/tangencia com a reta(restrição orçamentária). Ele corresponde à cesta de bens que maximiza a utilidade do consumidor frente à restrição orçamentária, dando-lhe maior satisfação.
No cálculo da cesta ótima, estamos diretamente tratando com o Problema do Consumidor. Esse problema consiste em se escolher a cesta que lhe proporcione a maior satisfação, ou seja, a cesta que maximize a sua utilidade dentro de uma restrição Orçamentária.
Existem diversas maneiras acerca de como calcular a cesta ótima. Vamos abordar a seguir as duas principais:
Nobres, ao usarmos esta forma de cálculo iremos nos deparar com o conceito de utilidade total e utilidade marginal. A Utilidade total possui nome sugestivo, ou seja, é a totalidade de Utilidade que aquela cesta de itens tem. Já a utilidade marginal surge a partir do comportamento que cada acréscimo de determinado bem causa. Ele é medido em unidades.
Suponhamos que não temos nenhum celular. Ao compramos o 1º celular, nossa utilidade total vai para 10u(unidades). Pois bem, ao comprarmos o 2º telefone, você percebe que sua satisfação(utilidade) aumentará, mas não aumentará tanto quanto da primeira?! E ao comprarmos o 3º celular, sua utilidade total também aumenta, pois você agora tem 3 celulares, mas o acréscimo de satisfação(utilidade marginal) foi menor – você não ficou tão entusiasmado. Em uma tabela, teríamos:
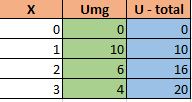
Por isso dizemos, como regra geral, que:
A Utilidade Total é crescente, mas a utilidade marginal é decrescente:
Voltando ao tópico, para o cálculo da cesta pela condição de equilíbrio, temos a seguinte fórmula:
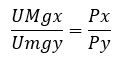
Umgx = Utilidade Marginal de x
Umgxy = Utilidade Marginal de y
Px e Py = Preço de X e Preço de Y.
Nobres, falou em “marginal”, falou em derivar. Ou seja, nessas questões você precisará derivar a função dada para encontrar a utilidade marginal. Não se assustem! Vamos usar a regrinha básica da derivação que ajudará a “matar” a maioria das questões. Temos um caso prático para entenderem:
Imaginemos a seguinte função da reta de restrição orçamentária:
R = Px. X + Py. Y, em que R é a renda e X e Y são as quantidades dos bens.
Se Px = 1; Py = 2, R = 10 e a Utilidade total de X,Y – U(X,Y) – Seja X.Y, quais as quantidades para a cesta ótima?
Vamos usar a fórmula:
Umgx/Umgy = Px/Py.
Para achar a Umgx, derivamos U = X.Y em função de X. Pessoal, a regrinha é: se é em função de X, o expoente de X, no caso 1, desce multiplicando X (1.X) e o seu expoente fica diminuído em 1. Ficamos assim com: 1.X1-1 . Y. No caso de Y, nada se faz pois ele é considerando uma constante(a derivação é em função de X). Assim, a UMGx = Y
Fazendo cálculo semelhante, a UMGy = X
Substituindo na fórmula, temos: Y/X = 1/2. Ou seja, X = 2.Y
Aí, pessoal, é só jogar na equação da restrição orçamentária:
10 = 1. X + 2.Y
10 = 1.2Y + 2Y; 4Y = 10; Y = 2,5.
Se Y=2,5, o X vale 2×2,5 = 5
A cesta ótima terá, então, 5 Unidades de X e 2,5 Unidades de Y.
A Função Cobb-Douglas é a queridinha das bancas, hein. Atenção a ela. Esta função apresenta a seguinte estrutura:
U(X,Y) = A.XαYβ , em que X e Y são os bens considerados. E alfa(α) e beta(β) são os expoentes.
Aqui, há uma fórmula, que nos ajuda no cálculo, sem precisar derivar:
X = α/( α + β) x R/Px
Y = β/( α + β) x R/Py
Aí, é só partir para o abraço! Vamos ilustrar com um exemplo que caiu na prova do IBGE 2016 – FGV
Anna é uma estudante do curso de Economia. No início do semestre ela precisa comprar dois itens para acompanhar suas aulas: folhas de fichário, X, e canetas, Y. Os preços de uma unidade desses bens são, respectivamente, pX = 5 e pY = 2. Se Anna tem renda de 60 unidades monetárias para cobrir os gastos do semestre com esses itens escolares e se sua função utilidade por esses bens é dada por U(X,Y) = 50X1/2Y1/2, a cesta ótima que pode ser comprada por Anna que maximiza sua utilidade sujeita a sua restrição orçamentária é:
Pessoal, sem pensar muito, como calcular a cesta ótima?
Comentários:
Obs. Iremos representar 1/2, por 0,5
X = 0,5/(0,5 + 0,5) x 60/5
Temos X = 0,5/1 x 12. Então, X=6
Da mesma forma, Y:
Y = 0,5/(0,5 +0,5) x 60/2. Então, Y = 15
Portanto, a cesta ótima será (6,15)
Finalizamos aqui mais um artigo. Vocês perceberam que para abordar o assunto e saber como calcular a “cesta ótima” tivemos que permear diversos outros temas da Teoria do Consumidor. Por fim, esperamos que seja de grande valia na caminhada de cada um.
Abraços e bons estudos!