Caros alunos, vejam a seguir a resolução das questões de Raciocínio Lógico dos diversos cargos do TRT 15. Espero que tenham ido muito bem!
FCC – TRT/15 – 2018) Em uma situação hipotética, um Tribunal julgou procedente o recurso de um jogador profissional que atua num clube do interior paulista, e manteve o reconhecimento da unicidade contratual no período de 5/8/2013 a 22/9/2015, desconsiderando, assim, a dispensa ocorrida em 27/7/2015. A decisão colegiada também aumentou de R$ 5 mil para R$ 32 mil a multa compensatória a ser paga pelo clube ao jogador, pela dispensa imotivada.
(Adaptado de: http://portal.trt15.jus.br/. Acessado em: 29/03/18)
De acordo com a notícia, o aumento percentual da multa compensatória a ser paga ao jogador foi de
(A) 185%.
(B) 156%.
(C) 540%.
(D) 640%.
(E) 590%.
RESOLUÇÃO:
A multa aumentou de 5 para 32 mil, ou seja, temos um aumento de 32 – 5 = 27 mil.
O aumento percentual é calculado assim:
Aumento percentual = aumento / valor inicial
Aumento percentual = 27 / 5 = 54 / 10 = 540/100 = 540%
Resposta: C
FCC – TRT/15 – 2018) Um curso de segurança do trabalho ministrado para servidores estaduais terá 35 horas de aula. Os servidores podem se inscrever nesse curso em módulos de duas aulas semanais de 1 hora e 10 minutos cada (opção 1), ou em módulos de três aulas semanais de 50 minutos cada (opção 2). Considerando que as duas opções de cursos iniciarão em uma segunda-feira e que não haverá feriados nas datas das aulas dos cursos, a opção de maior duração, em semanas, é a
(A) 1, superando a 2 em uma semana
(B) 1, superando a 2 em duas semanas.
(C) 2, superando a 1 em uma semana.
(D) 1 superando a 2 em três semanas.
(E) 2 superando a 1 em duas semanas.
RESOLUÇÃO:
No primeiro caso os alunos terão 2 aulas de 1h10min, ou seja, de 60 + 10 = 70 minutos, totalizando 2 x 70 = 140 minutos por semana.
No segundo caso os alunos terão 3 aulas de 50 minutos por semana, ou seja, 3×50 = 150 minutos por semana.
O tempo total dos cursos é de 35 horas, ou seja, 35×60 = 2100 minutos.
Dividindo o tempo total pelo número de minutos lecionados por semana, obteremos o total de semanas em cada caso. Veja:
Opção 1 = 2100 / 140 = 300 / 20 = 15 semanas
Opção 2 = 2100 / 150 = 210 / 15 = 70 / 5 = 140 / 10 = 14 semanas
Assim, a opção 1 supera a 2 em uma semana.
Resposta: A
FCC – TRT/15 – 2018) Para ser aprovado em um concurso, um candidato deve fazer uma prova de matemática, no valor de 25 pontos, uma prova de português, no valor de 30 pontos, e uma redação, no valor de 15 pontos. Zerar a pontuação em duas ou mais das três provas elimina o candidato. Além desse critério de eliminação, pontuação inferior a 15 pontos em qualquer uma das três provas também elimina o candidato, a menos que ele tenha obtido pontuação máxima em pelo menos uma das provas. De acordo com os dois critérios descritos, a menor pontuação total inteira que pode NÃO eliminar um candidato do concurso é igual a
(A) 30.
(B) 15.
(C) 16
(D) 25.
(E) 45.
RESOLUÇÃO:
É permitido zerar uma das provas. Assim, vamos zerar aquela de maior pontuação (português). Também vamos fazer apenas 1 ponto na prova de matemática. Neste caso, precisamos tirar nota máxima em redação, ficando com 0 + 1 + 15 = 16 pontos.
Este é o mínimo que podemos fazer para não sofrermos eliminação.
Resposta: C
FCC – TRT/15 – 2018) O consumo de combustível de um veículo utilizado no transporte de magistrados é de 8 km por litro de gasolina em uso urbano, e de 12 km por litro de gasolina com uso em estrada. No percurso entre os tribunais das cidades A e B, que estão a 90 km um do outro, 12 km são de trecho urbano e o restante é de trecho em estrada. Ao custo de R$ 4,20 por litro de gasolina, uma boa estimativa do gasto com combustível no transporte de um magistrado entre esses dois tribunais é de
(A) R$ 44,10.
(B) R$ 37,80.
(C) R$ 31,50.
(D) R$ 39,90.
(E) R$ 33,60
RESOLUÇÃO:
Temos 12km de trecho urbano e 90 – 12 = 78km de estrada. Para o trecho urbano, temos:
8km ———— 1 litro
12km ——— L litros
8.L = 12.1
L = 12/8 = 3/2 = 1,5 litro
Para o trecho de estrada temos:
12km ——– 1 litro
78km ——— M litros
12.M = 78.1
M = 78/12 = 39/6 = 13/2 = 6,5 litros
Ao todo temos 1,5 + 6,5 = 8 litros. Como o preço do litro é R$4,20, temos 8 x 4,20 = 33,60 reais.
Resposta: E
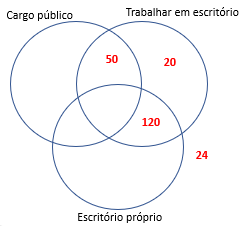
FCC – TRT/15 – 2018) Os 240 formandos de uma faculdade de Direito participaram de uma pesquisa que os inquiria sobre suas pretensões profissionais, de modo que podiam optar por nenhuma, uma ou mais das seguintes possibilidades: trabalhar em um escritório bem estabelecido, ingressar em um cargo público, abrir o próprio escritório. Os dados coletados foram os seguintes: − 10% não indicaram nenhuma das possibilidades contidas na pesquisa; − 30% almejam ingressar em um cargo público; − 50 têm interesse tanto em um cargo público quanto em trabalhar em um escritório bem estabelecido, mas não cogitam abrir seu próprio negócio; − 50% têm interesse em trabalhar em um escritório bem estabelecido ou em abrir seu próprio escritório, mas não se interessam por cargos públicos; − 20 têm interesse exclusivamente por trabalhar em um escritório bem estabelecido. Sendo assim, a quantidade daqueles que, entre esses formandos, têm interesse exclusivo por abrir seu próprio escritório é
(A) 8. (B) 16. (C) 24. (D) 4 (E) 12.
RESOLUÇÃO:
Temos o seguinte:
Temos o seguinte diagrama:
Ao todo temos 240 pessoas. Como queremos aquelas que querem SOMENTE abrir escritório próprio, podemos pegar o total (240) e tirar as que tem outros interesses (24), as que pretendem assumir algum cargo público (72), as que querem somente trabalhar em escritório (20) e as que querem somente trabalhar em escritório ou abrir um próprio (120), ficando:
SOMENTE abrir = 240 – 24 – 72 – 20 – 120 = 4
Resposta: D
FCC – TRT/15 – 2018) Os funcionários de um Tribunal estão alocados em 21 equipes de trabalho distintas, cada uma delas com pelo menos um funcionário. A média da quantidade de funcionários de cada uma dessas equipes é 13. Assim, a quantidade de funcionários da maior equipe de trabalho desse Tribunal é,
(A) no mínimo, 18.
(B) no máximo, 13.
(C) no mínimo, 14.
(D) no máximo, 26.
(E) no mínimo, 13
RESOLUÇÃO:
Se a média de funcionários por equipe é igual a 13, isto significa que pelo menos uma das equipes deve ter 13 ou mais funcionários. Isto permite marcar a alternativa E. Não podemos garantir que alguma equipe tenha MAIS de 13 funcionários, pois todas podem ter exatamente 13. Por outro lado, cada equipe tem, no mínimo, 1 funcionário.
Resposta: E
FCC – TRT/15 – 2018) André, Bruno, Carla e Daniela eram sócios em um negócio, sendo a participação de cada um, respectivamente, 10%, 20%, 20% e 50%. Bruno faleceu e, por não ter herdeiros naturais, estipulara, em testamento, que sua parte no negócio deveria ser distribuída entre seus sócios, de modo que as razões entre as participações dos três permanecessem inalteradas. Assim, após a partilha, a nova participação de André no negócio deve ser igual a
(A) 20%.
(B) 8%.
(C) 12,5%
(D) 15%.
(E) 10,5%.
RESOLUÇÃO:
Inicialmente André, Carla e Daniela possuíam, juntos, 10%+20%+50% = 80% do negócio. Ou seja, André possuía 10% de um total de 80% dos três. A fração dos 20% de Bruno que André deve ganhar é tal que:
Parte de André —————- Total
10% ——————————-80%
A ———————————– 20%
10%.20% = 80%.A
10%.20 = 80.A
10%.2 = 8.A
10% = 4.A
A = 2,5%
Assim, André passará a ter 2,5% + 10% = 12,5% do negócio.
Resposta: C
FCC – TRT/15 – 2018) Dez pastas diferentes devem ser guardadas em duas caixas diferentes. Se a única regra é que cada uma das caixas contenha pelo menos uma pasta, então a quantidade de maneiras distintas como se pode guardar essas pastas nas caixas é
(A) 510.
(B) 1022
(C) 126.
(D) 2048.
(E) 256.
RESOLUÇÃO:
Podemos escolher as pastas da primeira caixa fazendo a combinação das 10 pastas em grupos de 1, 2, 3, 4, 5, 6, 7, 8 ou 9 (não podemos pegar todas as 10). Temos:
PRIMEIRA CAIXA:
C(10,1) + C(10,2) + C(10,3) + C(10,4) + C(10,5) + C(10,6) + C(10,7) + C(10,8) + C(10,9) =
C(10,1) + C(10,2) + C(10,3) + C(10,4) + C(10,5) + C(10,4) + C(10,3) + C(10,2) + C(10,1) =
10 + 45 + 120 + 210 + 252 + 210 + 120 + 45 + 10 =
1022
Ao escolher as pastas da primeira caixa, automaticamente já definimos as pastas da segunda caixa também. Este é o gabarito.
Resposta: B
FCC – TRT/15 – 2018) A, B, C e D são alguns dos candidatos à presidência de um certo país. Um analista político, em entrevista a um programa de rádio, fez três previsões sobre o 1o turno das eleições:
− Se A ficar em primeiro lugar, então nem B e nem C ficarão entre os três primeiros.
− Se B ficar entre os três primeiros, então A não ficará entre os três primeiros.
− Se D ficar entre os três primeiros, então C ficará entre os três primeiros.
Assim, se A ficar em primeiro lugar no 1o turno e se as previsões do analista estiverem corretas, então, sobre B, C e D, pode-se concluir que
(A)certamente nenhum deles estará entre os três primeiros
(B) D poderá ou não estar entre os três primeiros.
(C) certamente apenas D estará entre os três primeiros.
(D) C ou D, mas não ambos, poderão estar entre os três primeiros.
(E) certamente apenas B e C não estarão entre os três primeiros.
RESOLUÇÃO:
Temos as premissas:
P1: Se A ficar em primeiro lugar, então nem B e nem C ficarão entre os três primeiros.
P2: Se B ficar entre os três primeiros, então A não ficará entre os três primeiros.
P3: Se D ficar entre os três primeiros, então C ficará entre os três primeiros.
P4: A ficou em primeiro.
Como P4 é proposição simples, começamos por ela, assumindo que A FICOU EM PRIMEIRO. Assim, em P1 vemos que NEM B NEM C FICARÃO ENTRE OS TRÊS PRIMEIROS.
Em P2, como “B ficar entre os três primeiros” é F, a frase já foi respeitada (é verdadeira).
Em P3, como a segunda parte é F, a primeira deve ser F também, ou seja, D NÃO FICA ENTRE OS TRÊS PRIMEIROS.
Com base nas conclusões em maiúsculas, podemos marcar a alternativa A.
Resposta: A
FCC – TRT/15 – 2018) Lúcio, Maurício e Júlio são sócios em uma empresa, sendo as partes de cada um: 15%, 25% e 60%, não necessariamente nessa ordem. Cada um dos sócios atua na empresa, mas em diferentes setores: Administração, Vendas e Informática. Além disso, sabe-se que: − o que atua na Administração não é o que tem 15% da empresa; − o que atua em Informática é amigo de infância do que tem 60%; − Júlio não atua em vendas; − quem atua em vendas é o sócio majoritário; − Lúcio tem 25% da empresa. Dessa forma, se a empresa está avaliada em R$ 120.000,00, então o valor da parte de Júlio é
(A) R$ 30.000,00.
(B) R$ 18.000,00
(C) R$ 72.000,00.
(D) R$ 36.000,00
(E) R$ 12.000,00.
RESOLUÇÃO:
Podemos montar a tabela:
| Sócio | Participação | Setor |
| Lúcio | 15%, 25% e 60% | Administração, Vendas e Informática |
| Maurício | 15%, 25% e 60% | Administração, Vendas e Informática |
| Júlio | 15%, 25% e 60% | Administração, Vendas e Informática |
Temos as informações:
− Júlio não atua em vendas;
− Lúcio tem 25% da empresa.
Até aqui ficamos com:
| Sócio | Participação | Setor |
| Lúcio | 25% | Administração, Vendas e Informática |
| Maurício | 15% e 60% | Administração, Vendas e Informática |
| Júlio | 15% e 60% | Administração e Informática |
Como quem atua em vendas é sócio majoritário, fica claro que Lúcio (que tem 25%) não atua em vendas. Note que o setor de vendas sobra para Maurício, que deve ter o percentual de 60%. Ficamos com:
| Sócio | Participação | Setor |
| Lúcio | 25% | Administração e Informática |
| Maurício | 60% | Vendas |
| Júlio | 15% | Administração e Informática |
Sabemos ainda que o que atua na Administração não é o que tem 15% da empresa, ou seja, não é Júlio, devendo ser Lúcio. Desta forma, sobra para Júlio a informática. Temos:
| Sócio | Participação | Setor |
| Lúcio | 25% | Administração |
| Maurício | 60% | Vendas |
| Júlio | 15% | Informática |
Se a empresa está avaliada em R$ 120.000,00, então o valor da parte de Júlio é 15% x 120.000 = 0,15 x 120.000 = 18.000 reais.
Resposta: B
FCC – TRT/15 – 2018) Em uma determinada seção de certa biblioteca, os livros são identificados por números naturais que vão de 100 a 362. Dentre esses livros, há 133 que estão emprestados. Sendo assim, é possível afirmar que, entre os livros emprestados, aqueles identificados por números consecutivos são, pelo menos,
(A) 3.
(B) 6.
(C) 2
(D) 4.
(E) 5.
RESOLUÇÃO:
O total de números que temos de 100 a 362 é de 362 – 100 + 1 = 263 livros. Veja que foi preciso somar 1 unidade, pois os DOIS extremos estão sendo considerados (100 e 362).
Como queremos a menor quantidade de livros com numeração consecutiva, podemos começar distribuindo os livros alternadamente: 100, 102, 104, 106 etc. O último será o 362. Até aqui, o total de livros distribuídos é de (362 – 100)/2 + 1 = 131+1 = 132. Veja que o próximo livro deverá ser colocado em posição entre outros dois. Assim, ficaremos com 3 livros consecutivos.
Uma outra interpretação é a seguinte: imagine que os números 100 e 101 são ocupados por dois livros. A partir daí, podemos seguir de dois em 2: 103, 105, 107 etc. Terminamos no 361. Até aí são (361 – 101)/2 + 1 = 131. Podemos pegar ainda o 362, ficando com todos os 133 livros (100, 101, 103, 105, 107, 109, …, 359, 361 e 362). Neste caso, só temos dois números consecutivos: 100-101 e 361-362.
Resposta: C
FCC – TRT/15 – 2018) Quando se diz que um imposto com alíquota de 20% incide sobre um produto cujo preço inicial é R$ 100,00, é usual concluir que, com o acréscimo desse imposto, o preço final do produto seria de R$ 120,00. Isso é chamado de cálculo “por fora”. Porém, há impostos em que se utiliza o chamado “cálculo por dentro”. Nesses casos, se uma alíquota de 20% incide sobre um produto cujo preço inicial é R$ 100,00, então o preço final é de R$ 125,00, pois 20% do valor final deve ser relativo ao imposto. Com um imposto de alíquota 18% sobre um produto cujo valor inicial é de R$ 1.640,00, a diferença entre os preços finais calculados por dentro e por fora é de
(A) R$ 128,40.
(B) R$ 32,40.
(C) R$ 360,00.
(D) R$ 64,80
(E) R$ 640,00.
RESOLUÇÃO:
Calculando o imposto “por fora”, ficamos com o preço final:
Preço final = 1640 x (1+18%) = 1640 x 1,18 = 1935,20 reais.
Calculando “por dentro”, podemos pensar assim:
Preço final – Imposto = Preço inicial
Chamando de “P” o preço final, temos:
P – 18%.P = 1640
0,82P = 1640
P = 1640/0,82
P = 2000 reais
A diferença é de 2000 – 1935,20 = 64,80
Resposta: D
FCC – TRT/15 – 2018) Um condomínio residencial com 12 apartamentos, cada um ocupado com apenas uma pessoa, pretende formar uma comissão para fazer uma auditoria de suas contas. Ficou decidido que essa comissão deve ter 2, 3, 4 ou 5 pessoas. Além disso, há exatamente 6 apartamentos cujos moradores declararam que não desejam participar da comissão; os demais não se opõem à participação. Dessa forma, a quantidade de possibilidades para a composição dessa comissão é
(A) 56
(B) 120.
(C) 15.
(D) 84.
(E) 67.
RESOLUÇÃO:
Temos 12 – 6 = 6 moradores que podem participar das comissões. Devemos somar os totais de comissões de 2, 3, 4 ou 5 pessoas, isto é:
C(6,2) + C(6,3) + C(6,4) + C(6,5) =
C(6,2) + C(6,3) + C(6,2) + C(6,1) =
15 + 20 + 15 + 6 =
56
Resposta: A
FCC – TRT/15 – 2018) Considere os dois argumentos a seguir:
I. Se Ana Maria nunca escreve petições, então ela não sabe escrever petições. Ana Maria nunca escreve petições. Portanto, Ana Maria não sabe escrever petições.
II. Se Ana Maria não sabe escrever petições, então ela nunca escreve petições. Ana Maria nunca escreve petições. Portanto, Ana Maria não sabe escrever petições.
Comparando a validade formal dos dois argumentos e a plausibilidade das primeiras premissas de cada um, é correto concluir que
(A) o argumento I é inválido e o argumento II é válido, mesmo que a primeira premissa de I seja mais plausível que a de II.
(B) ambos os argumentos são válidos, a despeito das primeiras premissas de ambos serem ou não plausíveis.
(C) ambos os argumentos são inválidos, a despeito das primeiras premissas de ambos serem ou não plausíveis.
(D) o argumento I é inválido e o argumento II é válido, pois a primeira premissa de II é mais plausível que a de I.
(E) o argumento I é válido e o argumento II é inválido, mesmo que a primeira premissa de II seja mais plausível que a de I
RESOLUÇÃO:
Vamos avaliar o primeiro argumento:
I. Se Ana Maria nunca escreve petições, então ela não sabe escrever petições. Ana Maria nunca escreve petições. Portanto, Ana Maria não sabe escrever petições.
Sendo verdade que Ana Maria nunca escreve petições, podemos voltar na primeira premissa e concluir que, de fato, ela não sabe escrever petições. Argumento VÁLIDO.
II. Se Ana Maria não sabe escrever petições, então ela nunca escreve petições. Ana Maria nunca escreve petições. Portanto, Ana Maria não sabe escrever petições.
Sendo verdade que Ana Maria nunca escreve petições, a primeira premissa já é verdadeira, independentemente de Ana Maria saber ou não escrever. Não podemos chegar na conclusão de que ela não sabe escrever petições. Argumento INVÁLIDO.
Resposta: E
Saudações.